The document discusses various circuit theorems including:
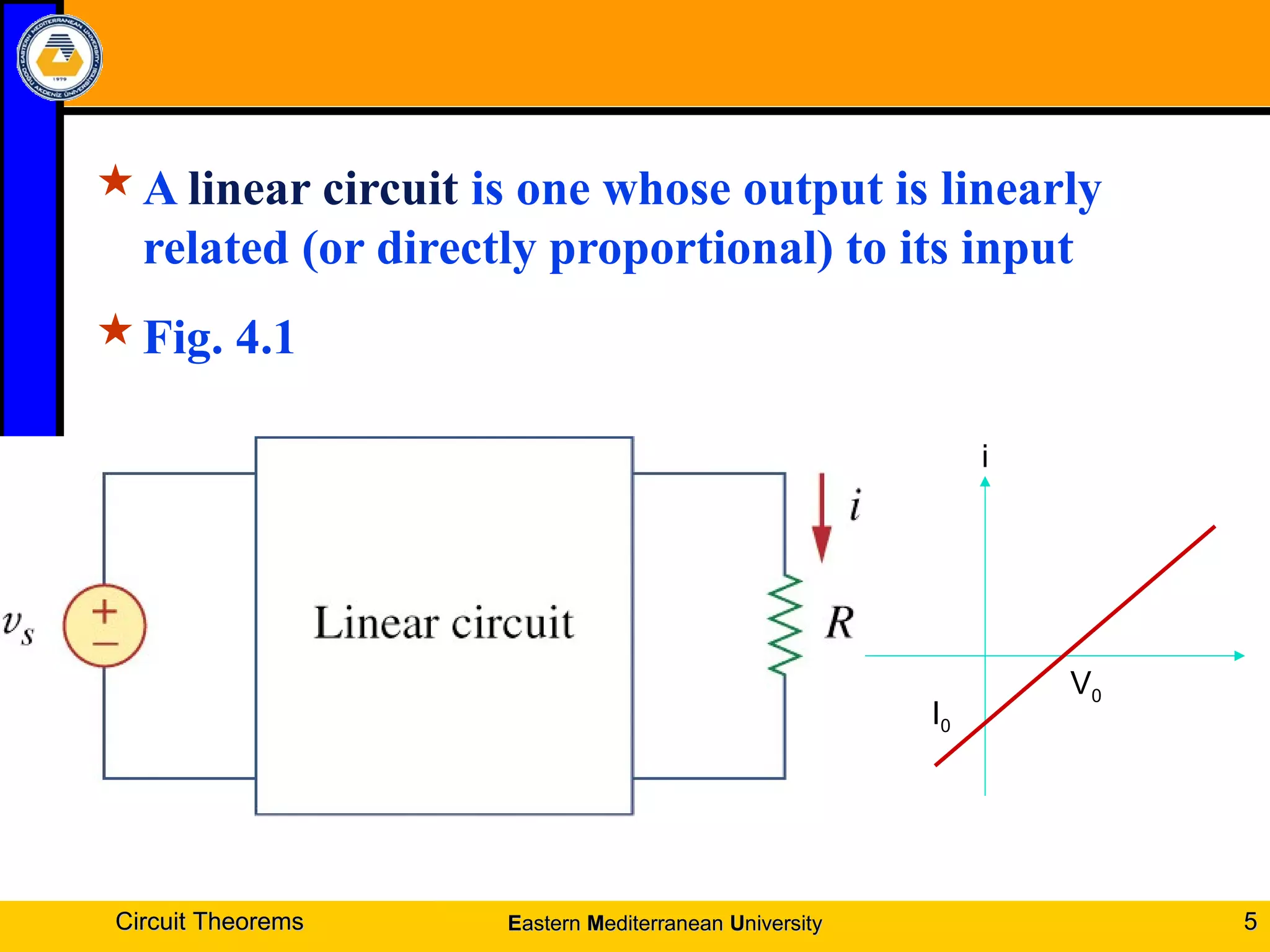
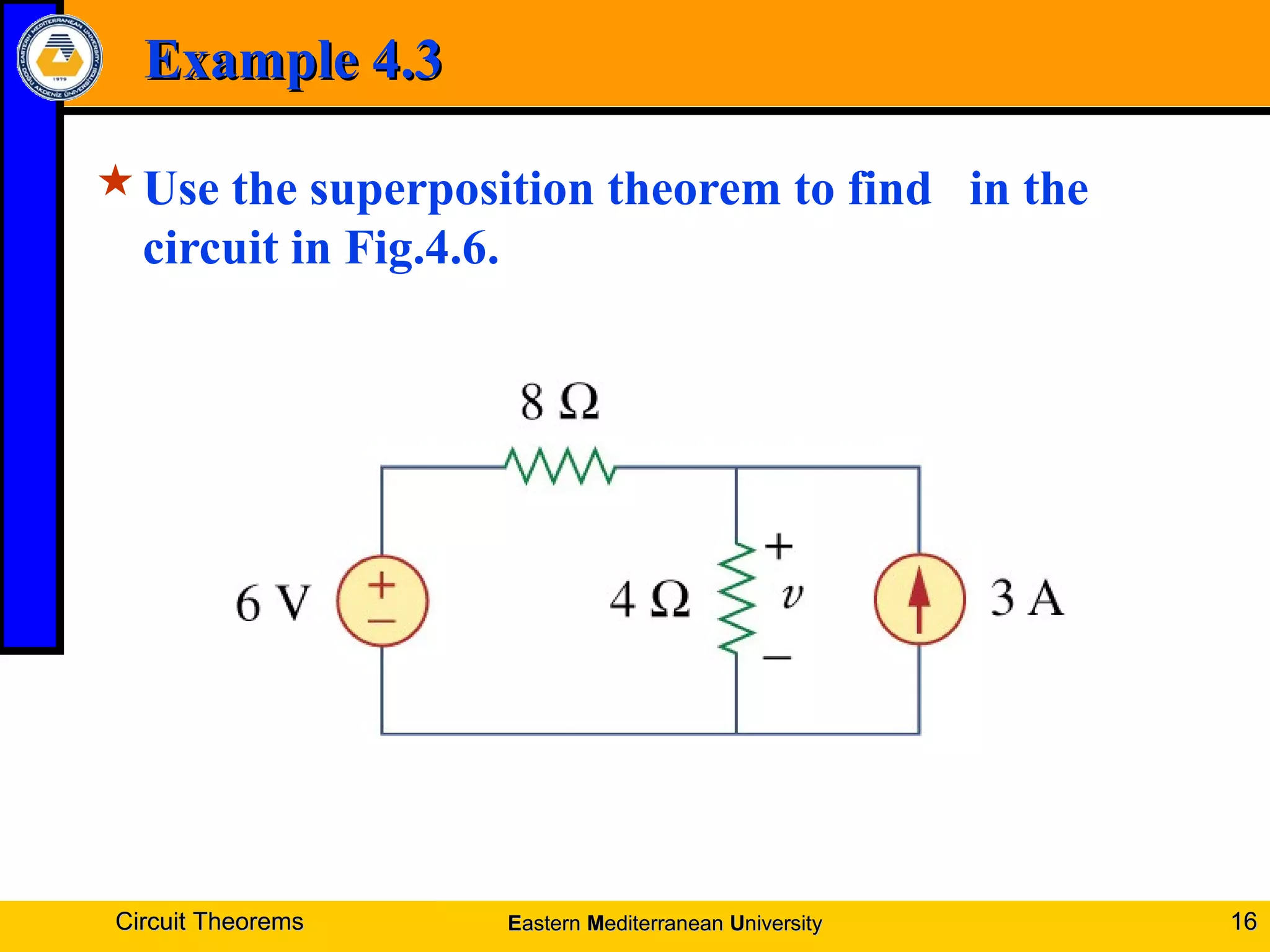
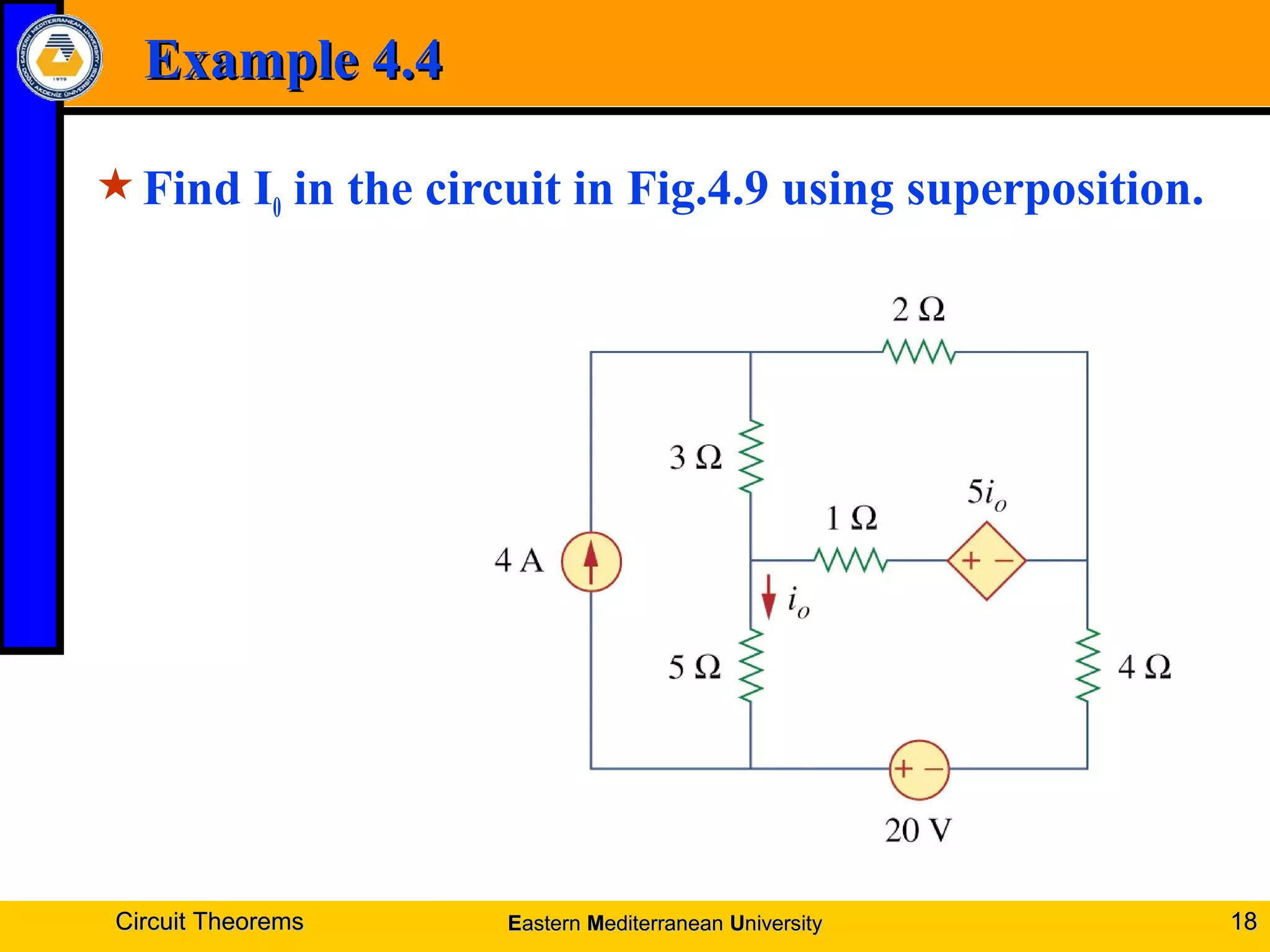
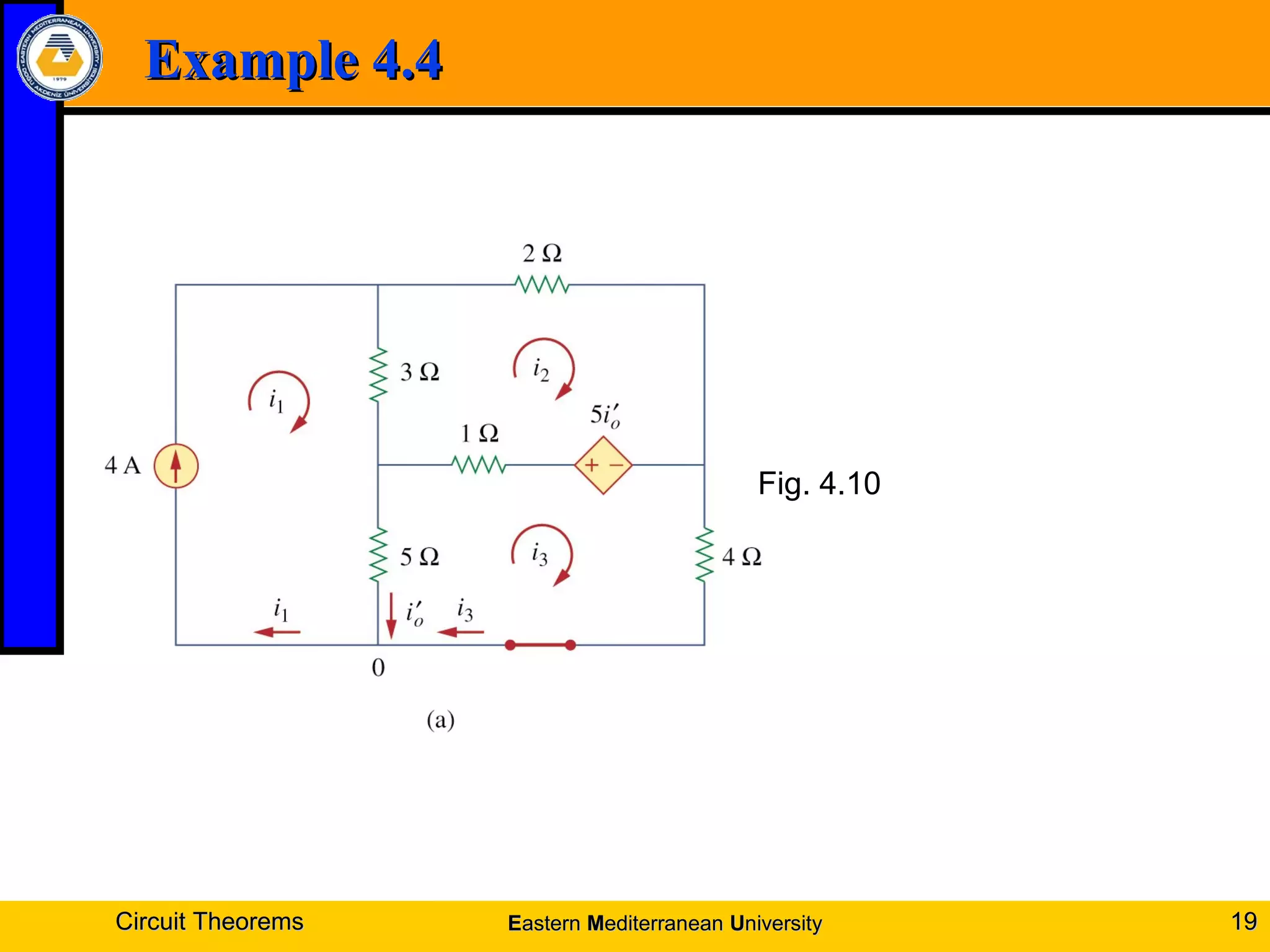
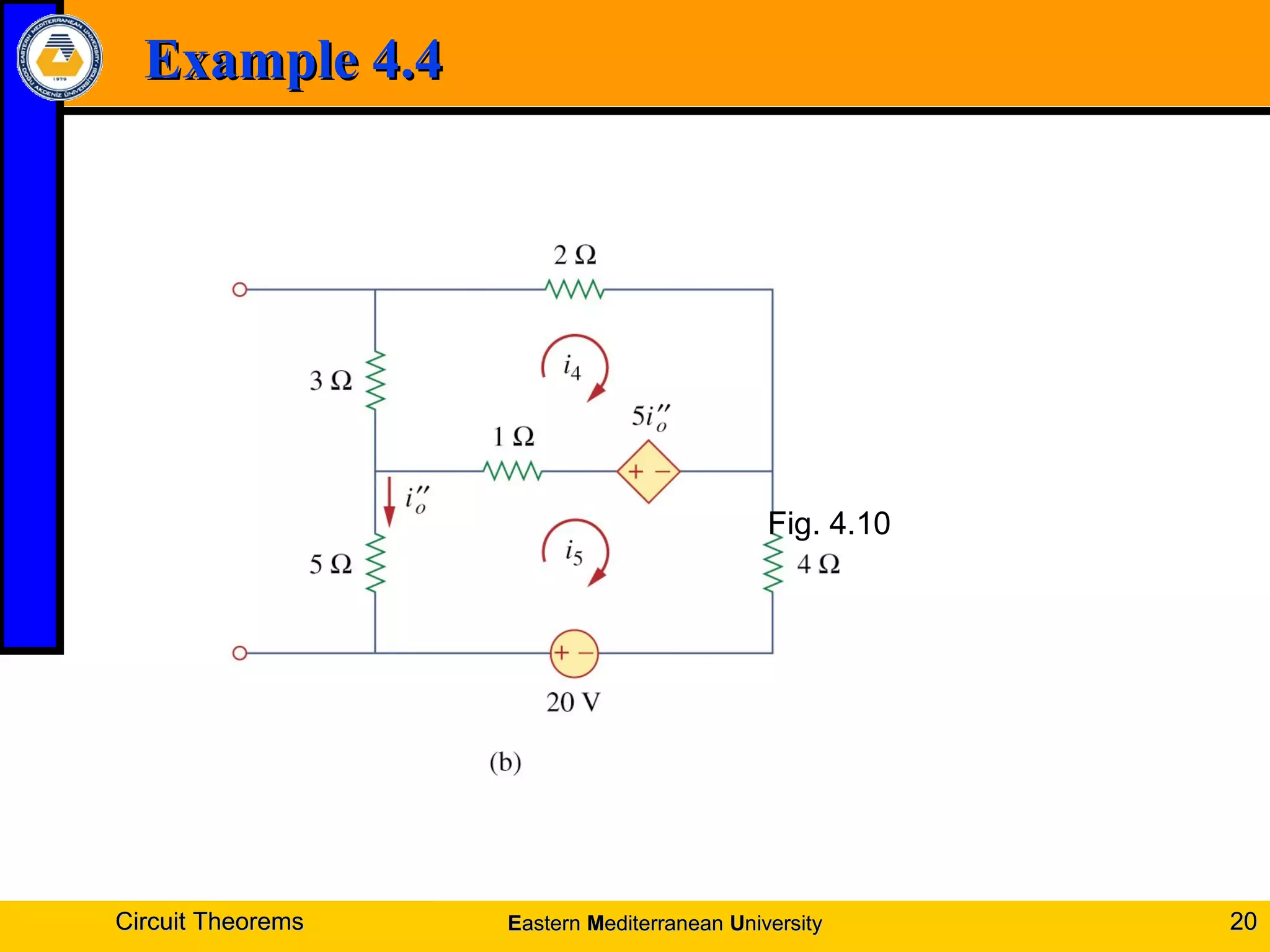
1. Linearity property and superposition principle which allow complex circuits to be simplified by treating sources individually.
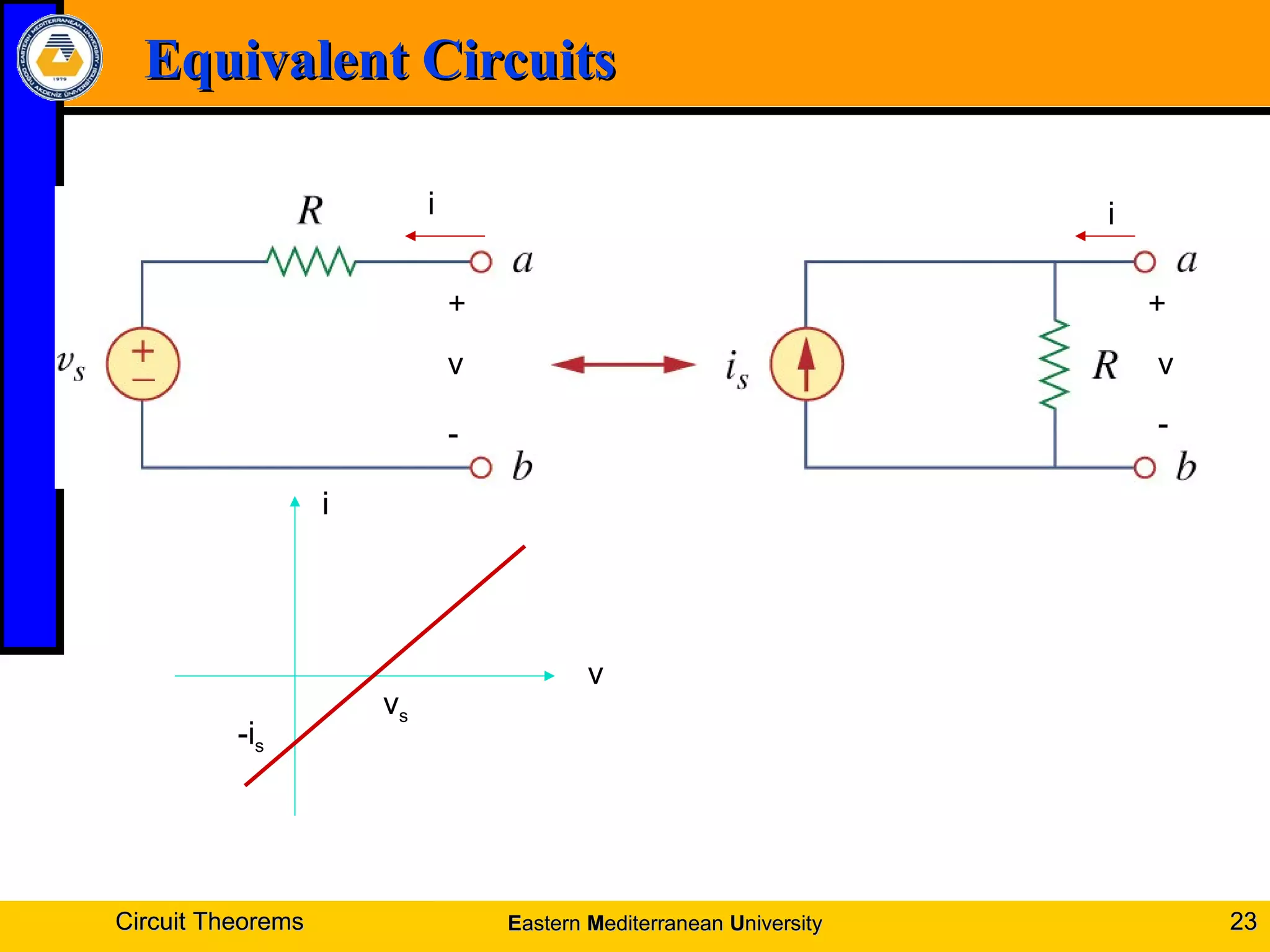
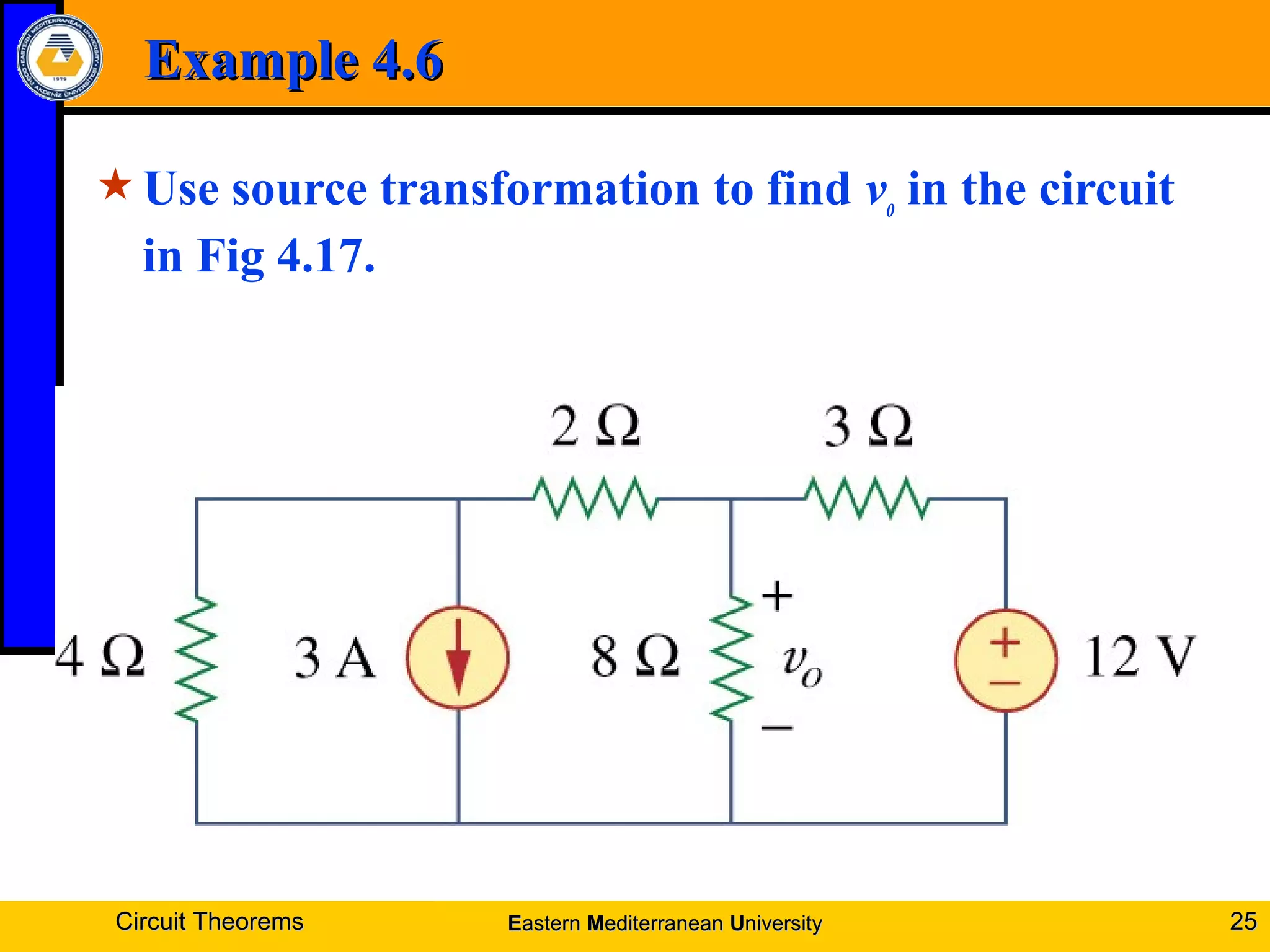
2. Source transformations allow replacing voltage sources in series with resistances by current sources in parallel with resistances.
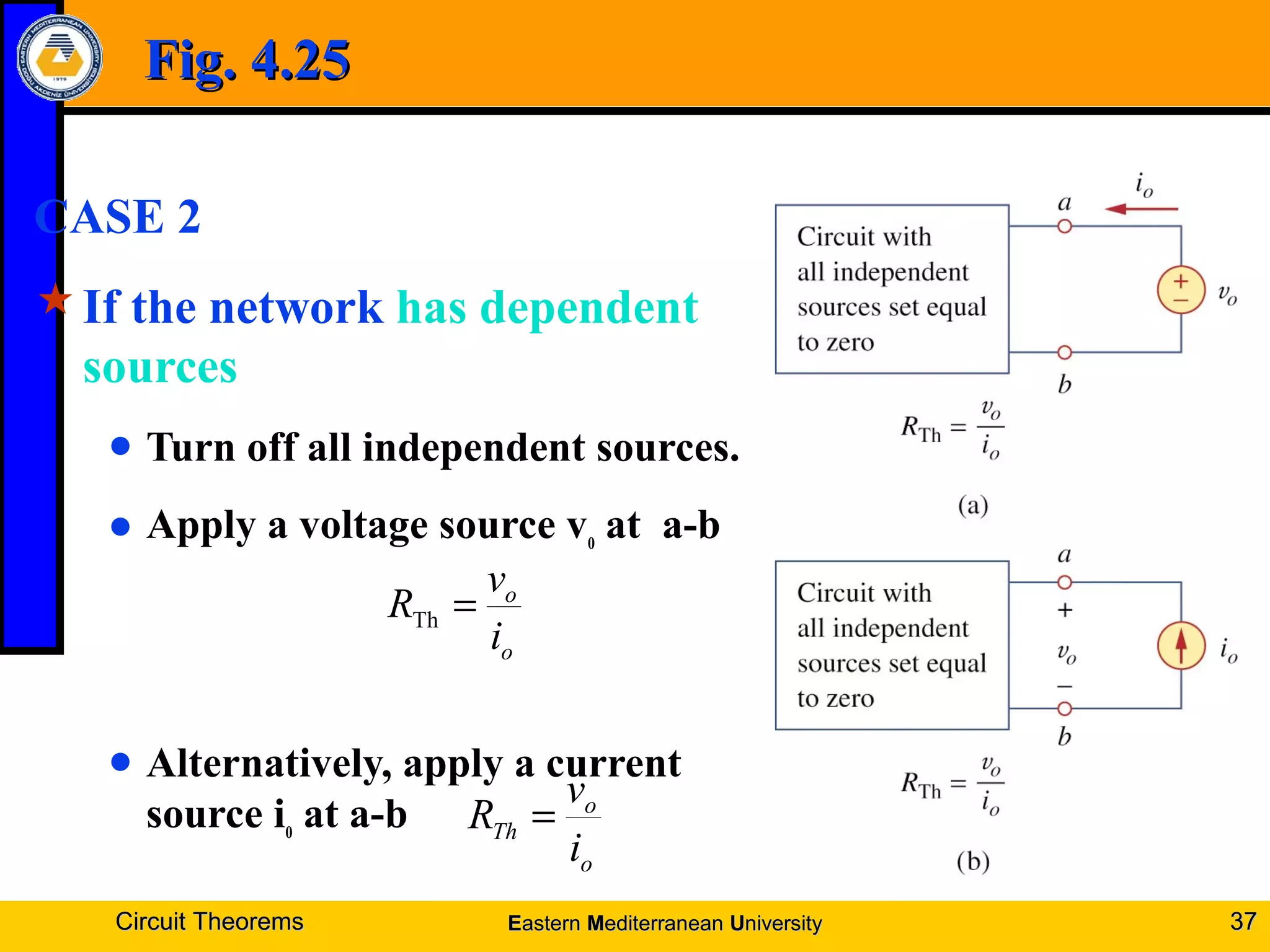
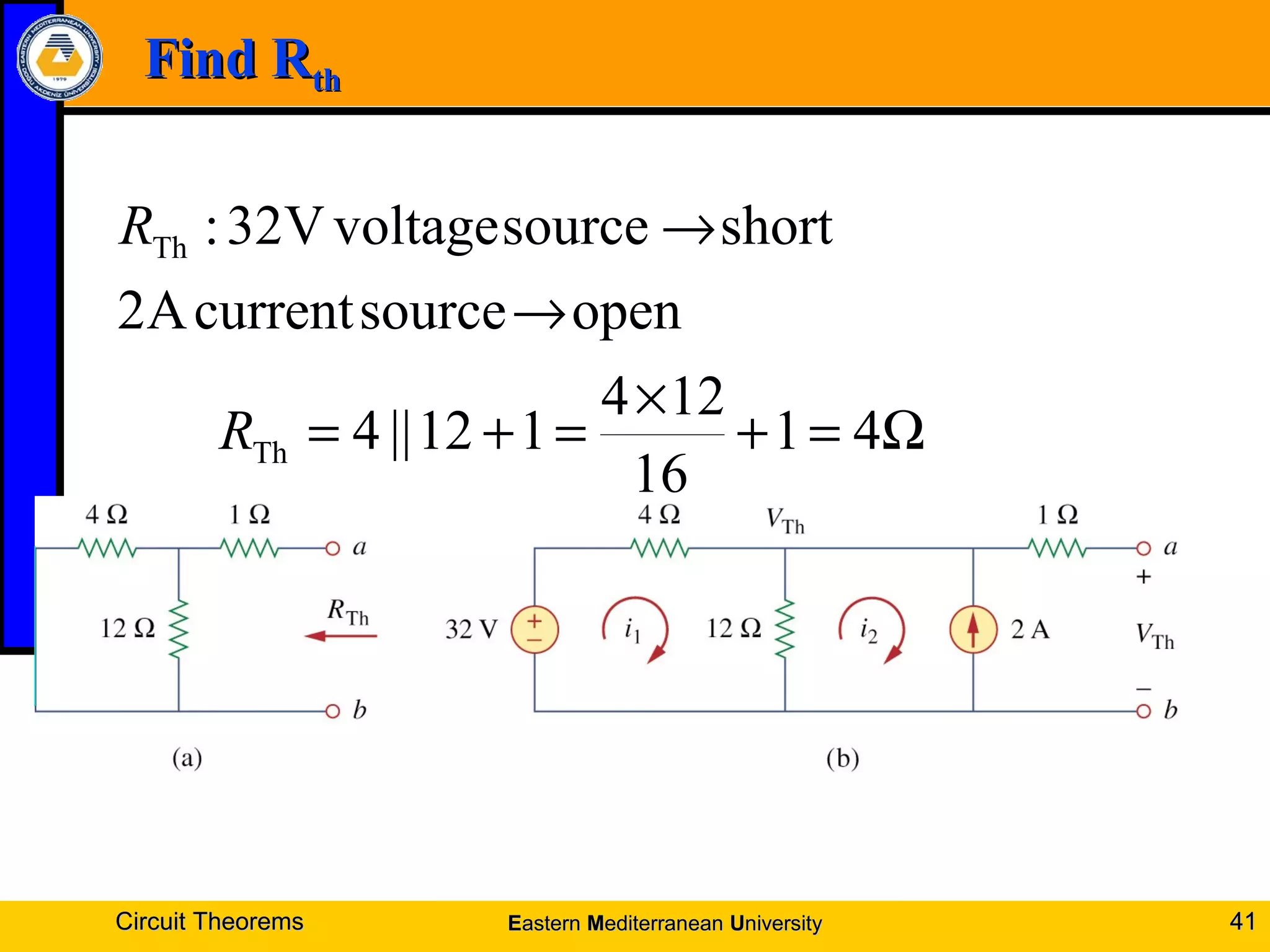
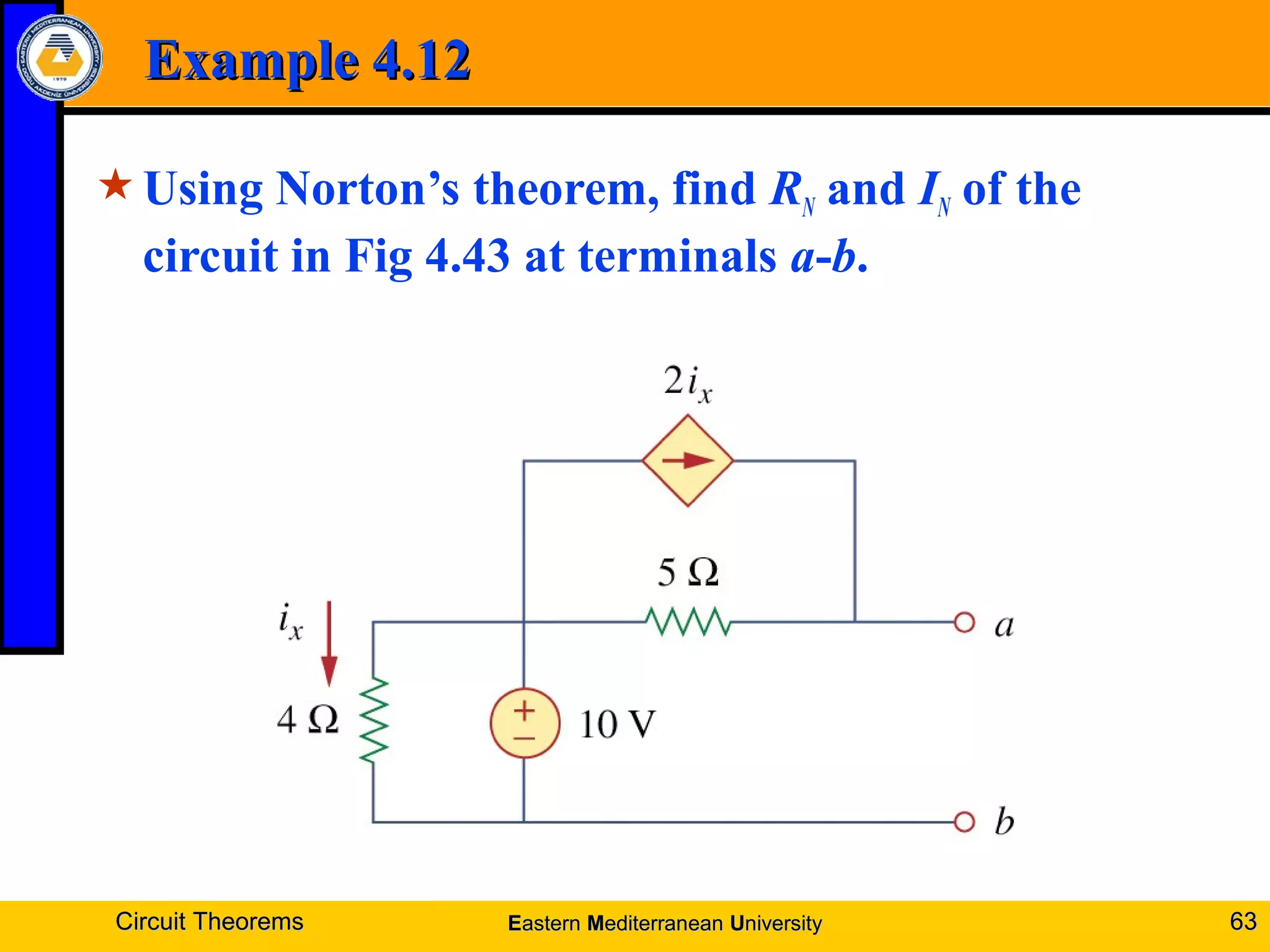
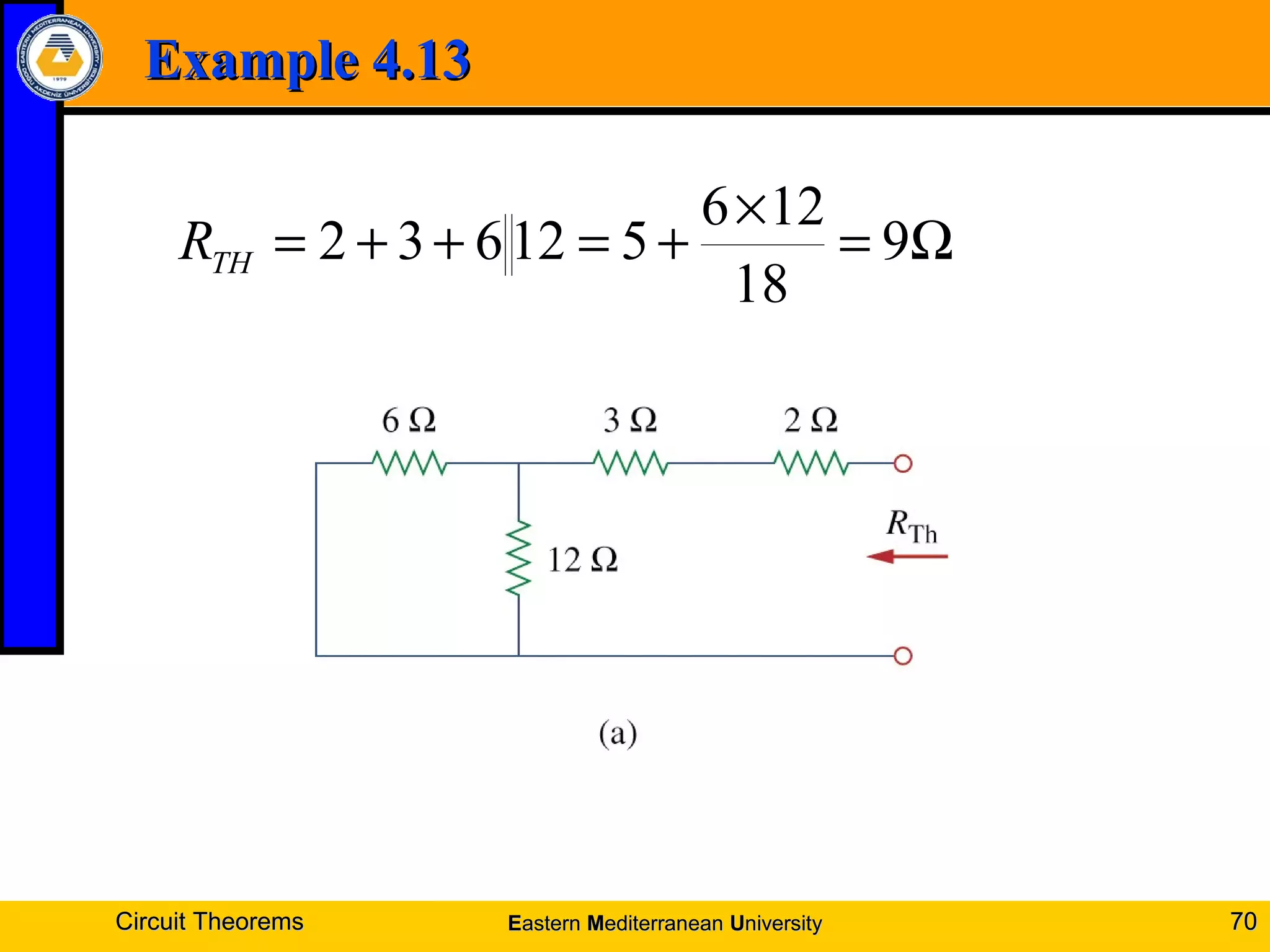
3. Thevenin's theorem states any linear two-terminal circuit can be reduced to a voltage source in series with a resistance.
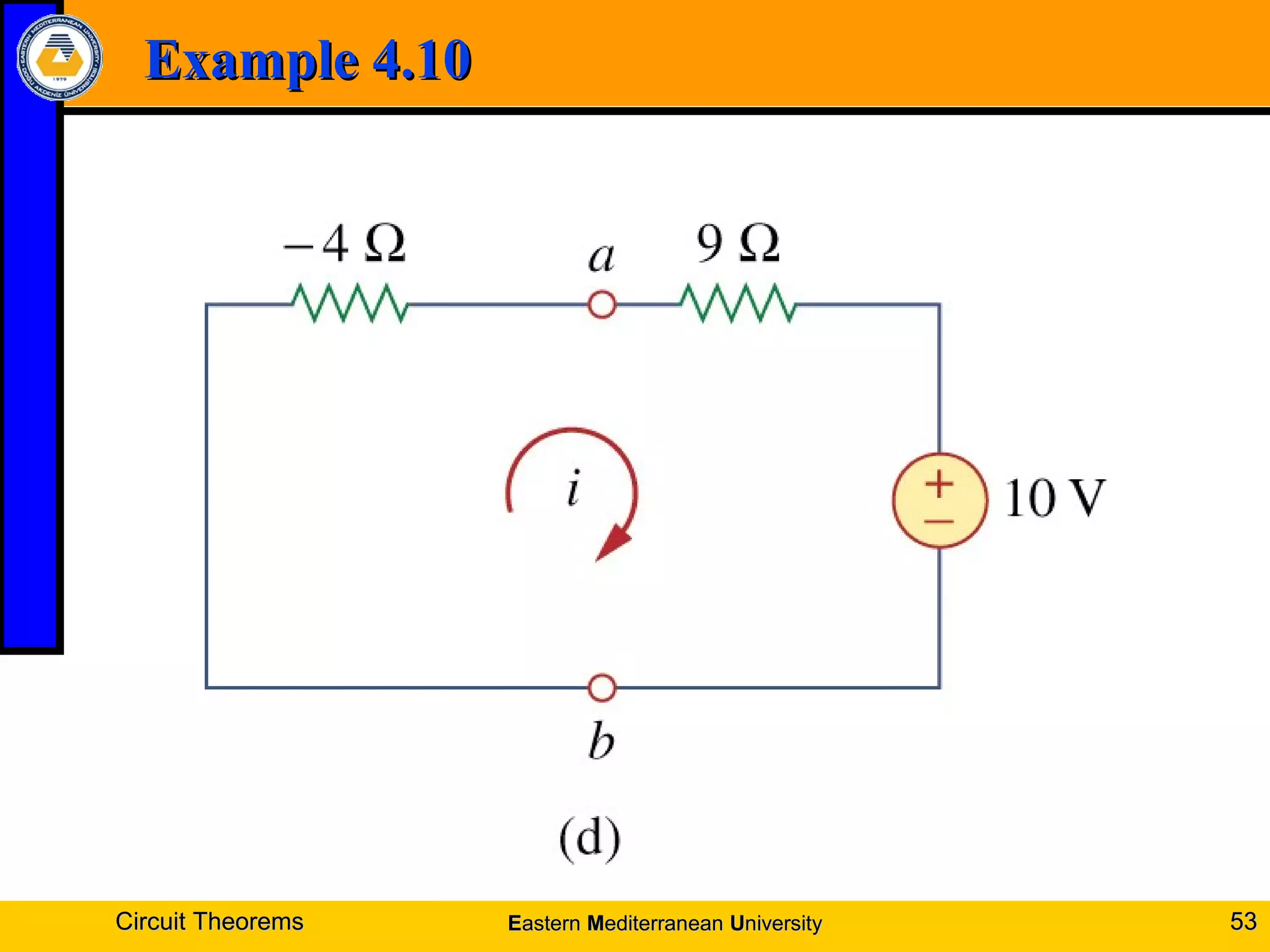
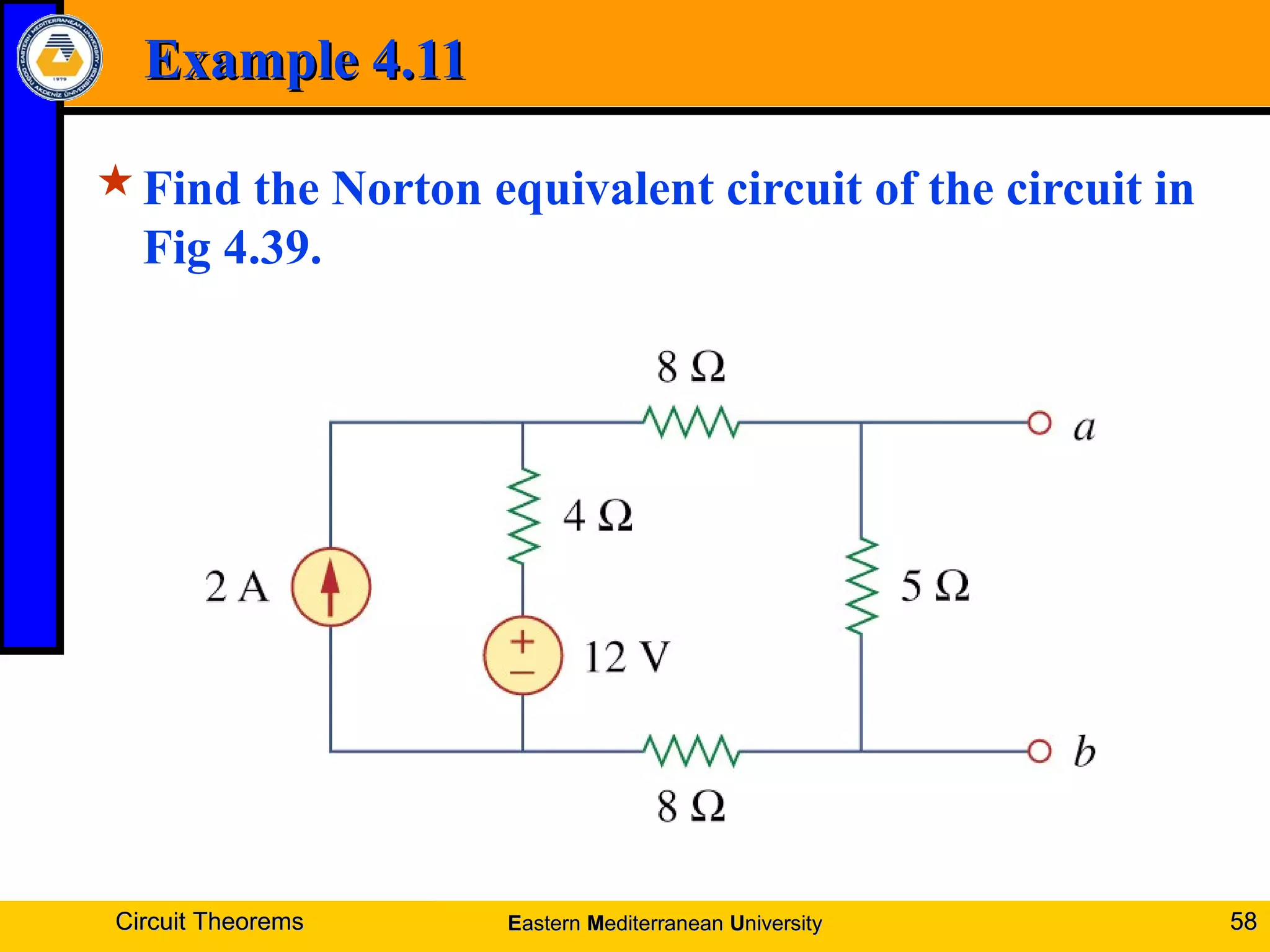
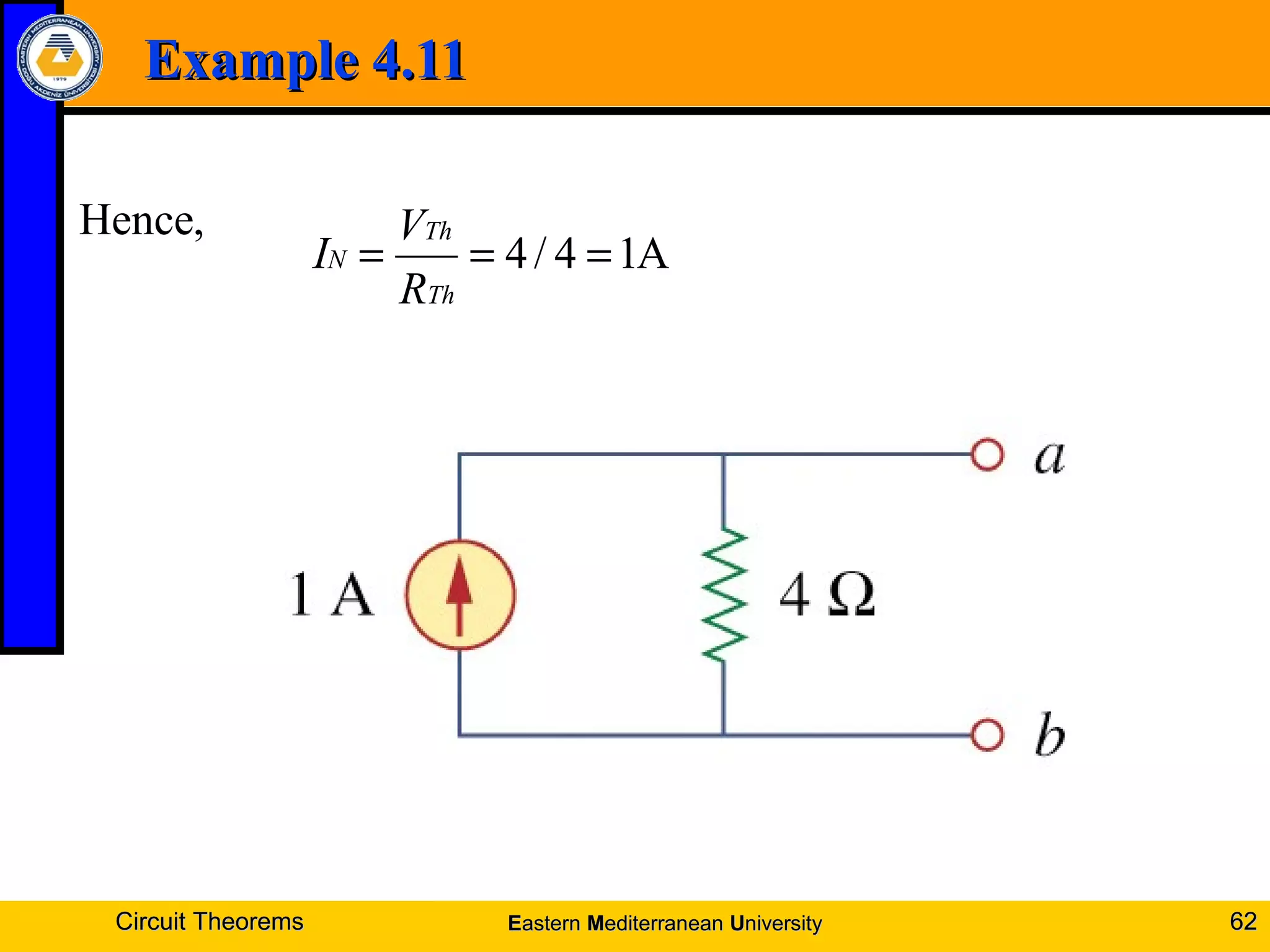
4. Examples are provided to demonstrate applying these theorems to solve for unknown voltages and currents.