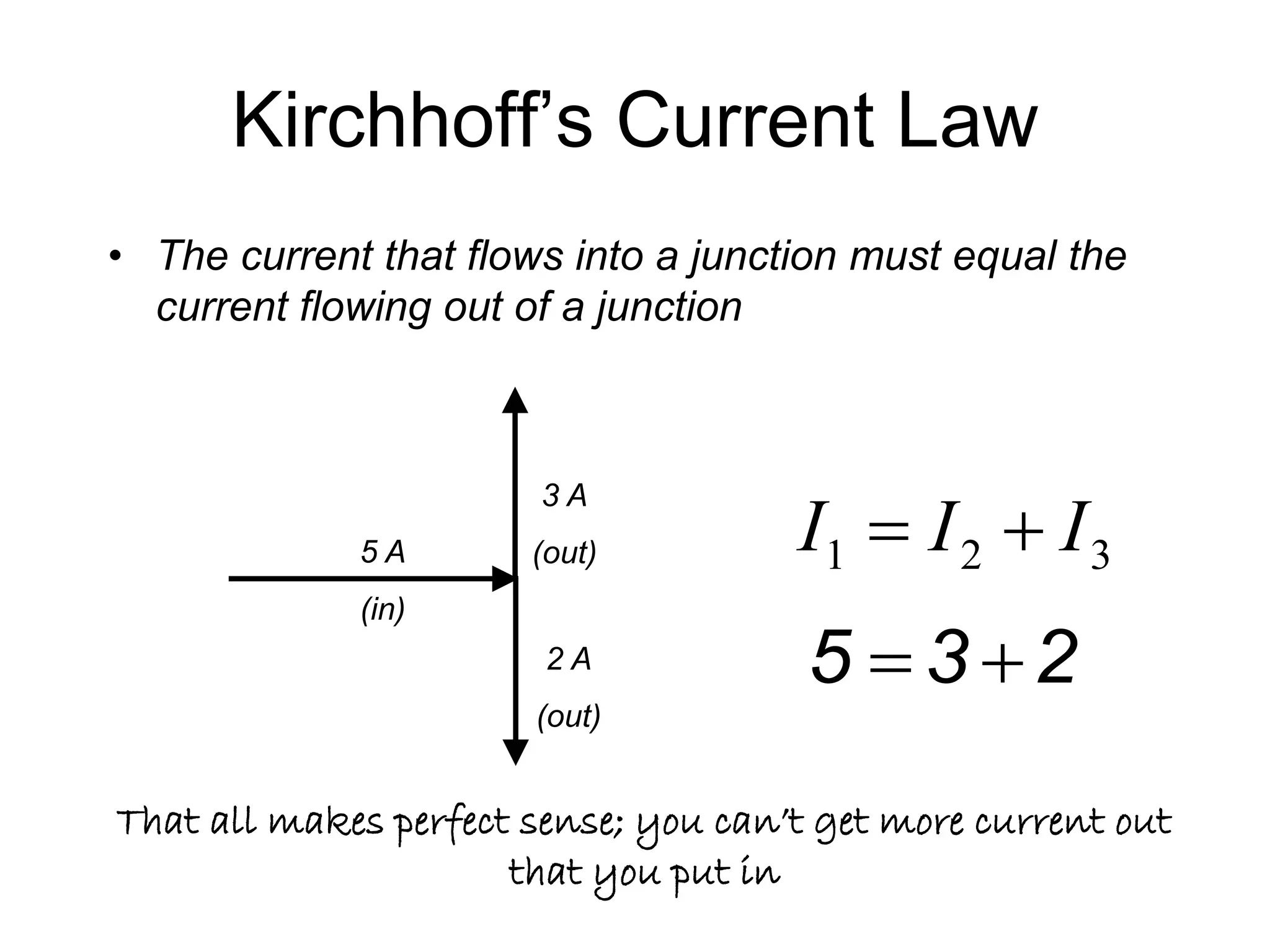
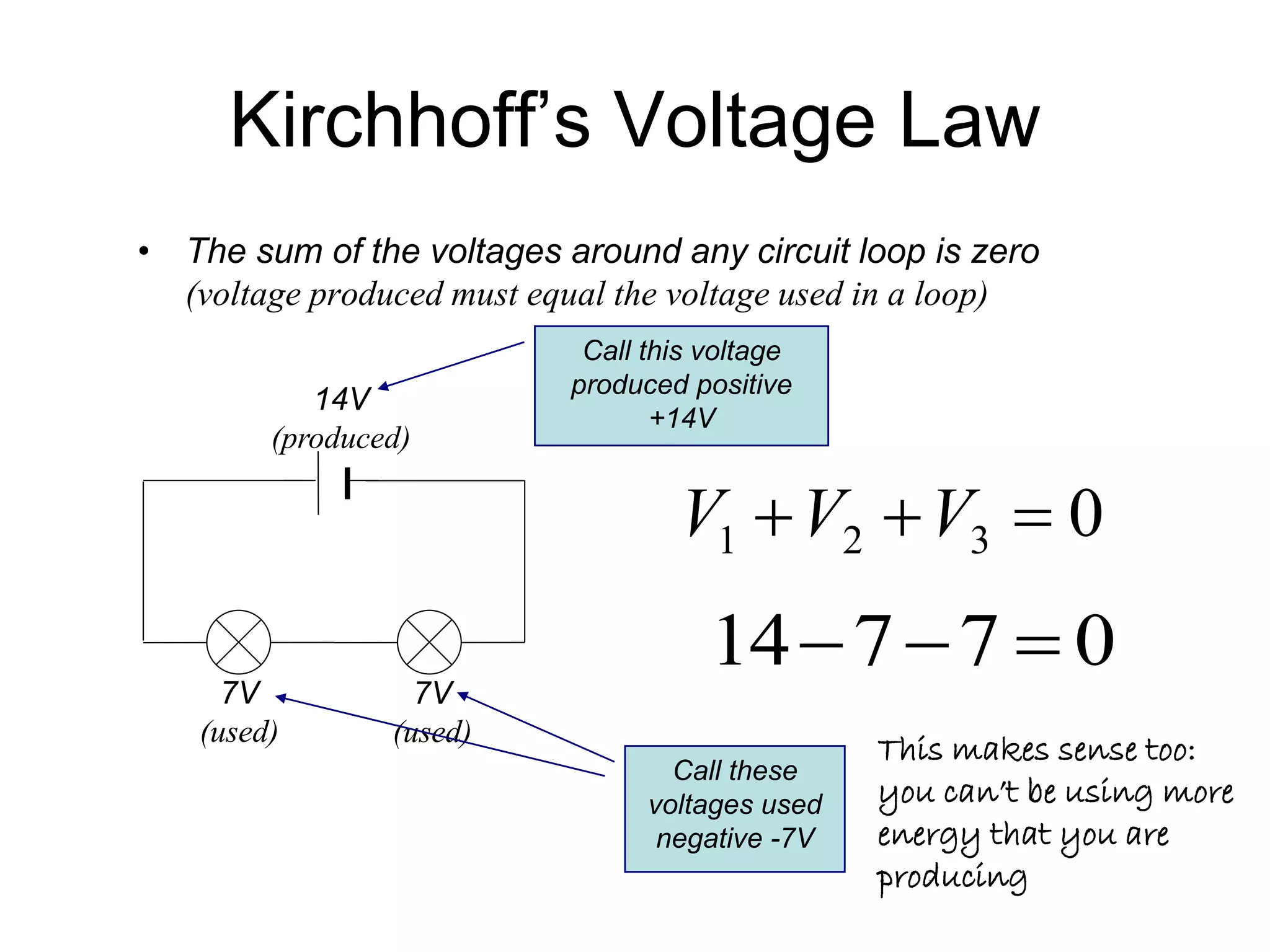
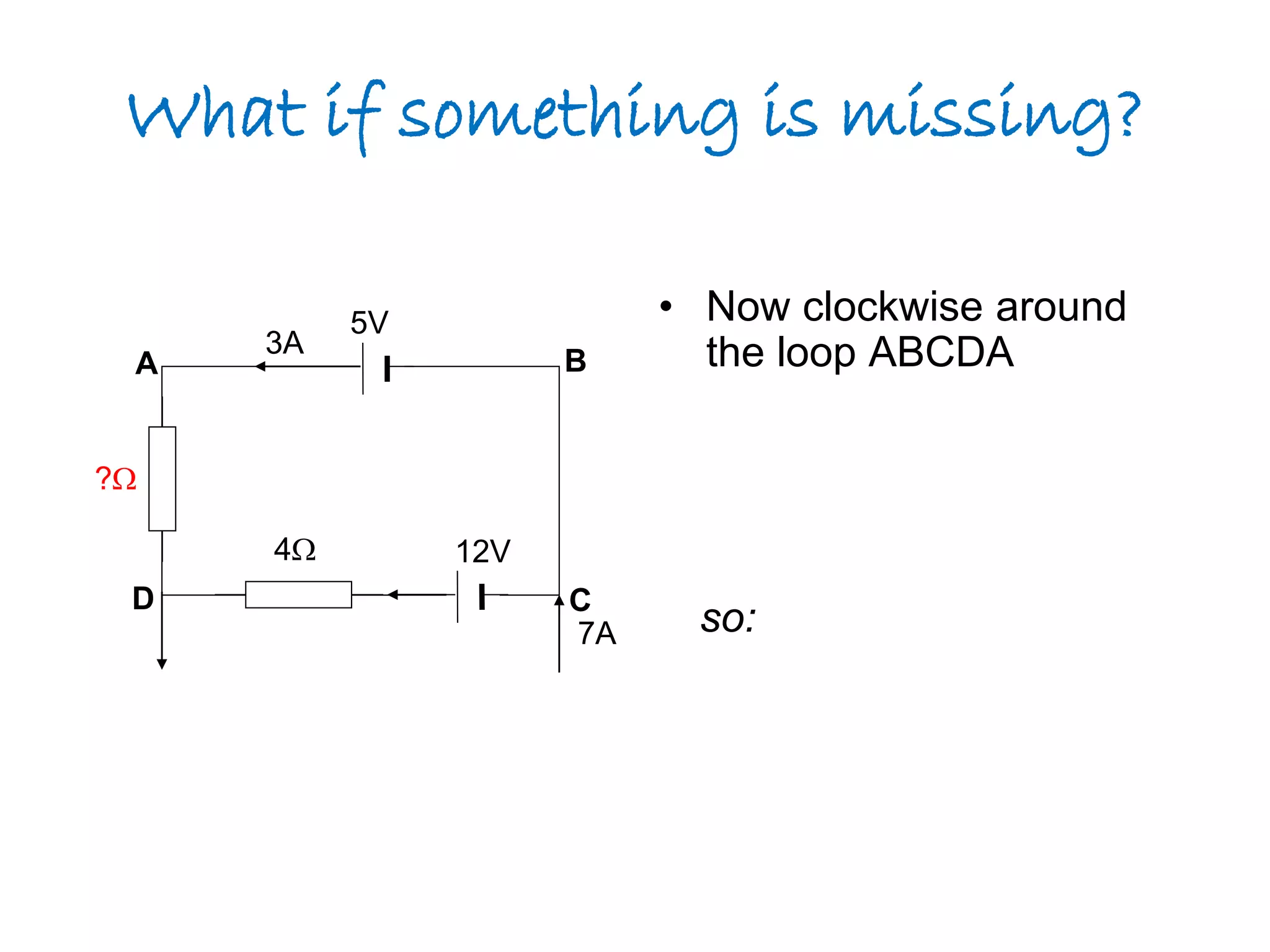
Kirchhoff's laws describe how electric current and voltage behave in circuits: 1) Kirchhoff's Current Law states that the total current entering a junction must equal the total current leaving it. 2) Kirchhoff's Voltage Law states that the sum of the voltages around any closed circuit loop is equal to zero. The voltage provided must equal the voltage used. 3) These laws allow analysis of complex circuits involving multiple batteries, cells, and circuit components by systematically tracing loops and applying the rules that voltage is positive when traveling in the direction of conventional current and negative when traveling opposite.

1. Kirchhoff’s Laws
What goes in must come
out

2. Kirchhoff’s Current Law
• The current that flows into a junction must equal the
current flowing out of a junction
3 A
(out)
1 2 3 I  I  I 5 A
(in)
2 A
(out)
5  3 2
That all makes perfect sense; you can’t get more current out
that you put in

3. Kirchhoff’s Voltage Law
• The sum of the voltages around any circuit loop is zero
(voltage produced must equal the voltage used in a loop)
1 2 3 0 V V V 
14V
(produced)
7V
(used)
7V
(used)
Call this voltage
produced positive
+14V
1477  0
Call these
voltages used
negative -7V
This makes sense too:
you can’t be using more
energy that you are
producing

4. Getting more complex
• Some loops involve more than one cell or battery and
several components.
• It is important to work your way around a loop
systematically in one direction (doesn’t matter which way you go
as long as you keep going in the same direction around the whole loop)

5. The Rules -Cells
1. Passing through a cell in the same direction as
conventional current is a positive voltage (energy
produced)
12V
I
2. Passing through a cell in the opposite direction to
conventional current 12V
is a negative voltage (energy used)
I
+12V
-12V

6. The Rules -Components
1. Passing through a component in the same direction as
conventional current is a negative voltage (energy used)
-12V
2. Passing through a component in the opposite direction
to conventional current is a positive voltage (energy
gained)
+12V

7. Putting it all together
• Working anticlockwise
around the loop ABCDA
AB +15V
BC –(2X11)V
(V=IR)
CD +(4X3)V -5V
so:
+15 - 22 +12 – 5 = 0
2A
15V
4 5V
11
B A
C D
5A

8. Try the other direction
5A
2A
15V
4 5V
11
B A
C D
• Now clockwise around
the loop BADCB
BA -15V
DC +5V –(4X3)V
(V=IR)
CB +(11X2)V
so:
-15 + 5 - 12 + 22 = 0

9. Try this;
• Working anticlockwise
around the loop ABCDA
AB +15V
BC –(1.5X40)V
(V=IR)
CD +(2.5X20)V -5V
so:
+15 - 60 +50 – 5 = 0
4A
15V
20 5V
40
B A
2.5A
C D

10. What if something is missing?
A B
7A
3A
5V
4 12V
?
D C
• Now clockwise around
the loop ABCDA
AB -5V
CD +12V –(4X4)V
(V=IR)
DA +(3XR)V
so:
-5 + 12 – 16 + 3R = 0
3R=9
R=3 

11. or this one…
• Now clockwise around
the loop ABCDA
AB -15V
CD + V –(0.5X80)V
(V=IR)
DA +(1.5X30)V
so:
-15 + V – 40 + 45 = 0
V=10V
15V
80 ?V
0.5A
30
A B
D C
2A

12. Now some Exercises
• Try ESA, Activity 13C, Pg 214
• ABA, Pg 134-136

13. Homework