This document provides an introduction to solving inequalities. It begins with essential questions and key vocabulary related to inequalities, including set-builder and interval notation. It then shows four examples of solving different types of one-step and multi-step inequalities. Each example solves the inequality, expresses the solution set using set-builder and interval notation, and graphs it on a number line. The examples demonstrate how to isolate the variable, determine if the inequality sign flips, and write the solution set in the two different notations.














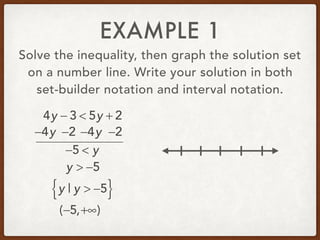









































![EXAMPLE 5
Solve the inequality, then graph the solution set
on a number line. Write your solution in both
set-builder notation and interval notation.
7 < x + 2 ≤ 11
x + 2 > 7 and x + 2 ≤ 11
−2 −2 −2 −2
x > 5 and x ≤ 9
5 < x ≤ 9
x | 5 < x ≤ 9{ }
(5,9]](https://image.slidesharecdn.com/alg2section1-2-171107014904/85/Algebra-2-Section-1-2-58-320.jpg)
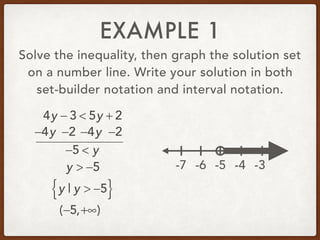
![EXAMPLE 5
Solve the inequality, then graph the solution set
on a number line. Write your solution in both
set-builder notation and interval notation.
7 < x + 2 ≤ 11
x + 2 > 7 and x + 2 ≤ 11
−2 −2 −2 −2
x > 5 and x ≤ 9
5 < x ≤ 9
x | 5 < x ≤ 9{ }
(5,9]](https://image.slidesharecdn.com/alg2section1-2-171107014904/85/Algebra-2-Section-1-2-59-320.jpg)
![EXAMPLE 5
Solve the inequality, then graph the solution set
on a number line. Write your solution in both
set-builder notation and interval notation.
7 < x + 2 ≤ 11
x + 2 > 7 and x + 2 ≤ 11
−2 −2 −2 −2
x > 5 and x ≤ 9
5 < x ≤ 9
x | 5 < x ≤ 9{ }
(5,9]
5 6 7 8 9](https://image.slidesharecdn.com/alg2section1-2-171107014904/85/Algebra-2-Section-1-2-60-320.jpg)
![EXAMPLE 5
Solve the inequality, then graph the solution set
on a number line. Write your solution in both
set-builder notation and interval notation.
7 < x + 2 ≤ 11
x + 2 > 7 and x + 2 ≤ 11
−2 −2 −2 −2
x > 5 and x ≤ 9
5 < x ≤ 9
x | 5 < x ≤ 9{ }
(5,9]
5 6 7 8 9](https://image.slidesharecdn.com/alg2section1-2-171107014904/85/Algebra-2-Section-1-2-61-320.jpg)
![EXAMPLE 5
Solve the inequality, then graph the solution set
on a number line. Write your solution in both
set-builder notation and interval notation.
7 < x + 2 ≤ 11
x + 2 > 7 and x + 2 ≤ 11
−2 −2 −2 −2
x > 5 and x ≤ 9
5 < x ≤ 9
x | 5 < x ≤ 9{ }
(5,9]
5 6 7 8 9](https://image.slidesharecdn.com/alg2section1-2-171107014904/85/Algebra-2-Section-1-2-62-320.jpg)
![EXAMPLE 5
Solve the inequality, then graph the solution set
on a number line. Write your solution in both
set-builder notation and interval notation.
7 < x + 2 ≤ 11
x + 2 > 7 and x + 2 ≤ 11
−2 −2 −2 −2
x > 5 and x ≤ 9
5 < x ≤ 9
x | 5 < x ≤ 9{ }
(5,9]
5 6 7 8 9](https://image.slidesharecdn.com/alg2section1-2-171107014904/85/Algebra-2-Section-1-2-63-320.jpg)
![EXAMPLE 6
Graph the solution set on a number line.
(−∞,5]∪ (7,+∞)](https://image.slidesharecdn.com/alg2section1-2-171107014904/85/Algebra-2-Section-1-2-64-320.jpg)
![EXAMPLE 6
Graph the solution set on a number line.
(−∞,5]∪ (7,+∞)](https://image.slidesharecdn.com/alg2section1-2-171107014904/85/Algebra-2-Section-1-2-65-320.jpg)
![EXAMPLE 6
Graph the solution set on a number line.
(−∞,5]∪ (7,+∞)
5 6 7 84](https://image.slidesharecdn.com/alg2section1-2-171107014904/85/Algebra-2-Section-1-2-66-320.jpg)
![EXAMPLE 6
Graph the solution set on a number line.
(−∞,5]∪ (7,+∞)
5 6 7 84](https://image.slidesharecdn.com/alg2section1-2-171107014904/85/Algebra-2-Section-1-2-67-320.jpg)
![EXAMPLE 6
Graph the solution set on a number line.
(−∞,5]∪ (7,+∞)
5 6 7 84](https://image.slidesharecdn.com/alg2section1-2-171107014904/85/Algebra-2-Section-1-2-68-320.jpg)
![EXAMPLE 6
Graph the solution set on a number line.
(−∞,5]∪ (7,+∞)
5 6 7 84](https://image.slidesharecdn.com/alg2section1-2-171107014904/85/Algebra-2-Section-1-2-69-320.jpg)
![EXAMPLE 6
Graph the solution set on a number line.
(−∞,5]∪ (7,+∞)
5 6 7 84](https://image.slidesharecdn.com/alg2section1-2-171107014904/85/Algebra-2-Section-1-2-70-320.jpg)

