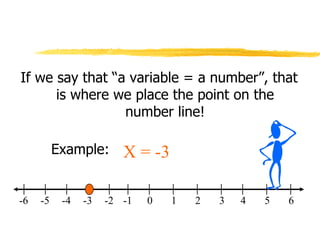
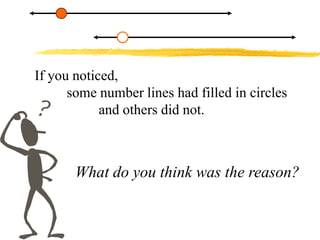
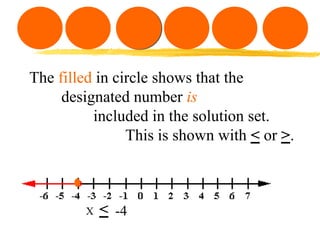
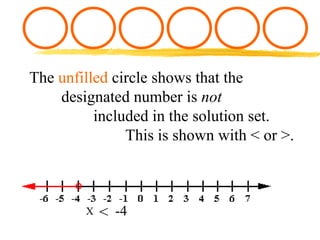
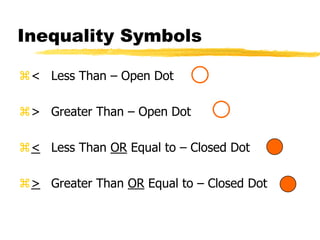
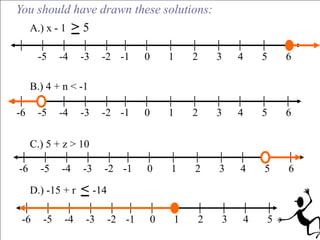
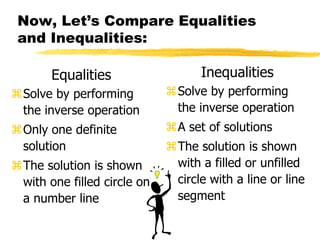
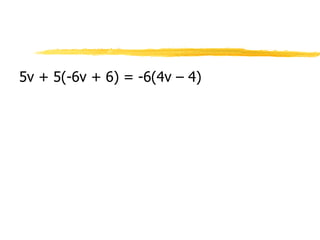This document discusses graphing equations and inequalities on a number line. It explains that an equality has one definite solution which is shown as a filled circle, while an inequality gives a set of solutions shown with open or closed circles depending on whether it is <, >, ≤, or ≥. Examples are given of solving various equations and inequalities algebraically and graphing the solutions on a number line. The key differences between equalities and inequalities are outlined.

1. Graphing Equations and
Inequalities

2. POD
Distribute
1) 5(-6b + 6)
2) -6(4r – 4)
Combine Like Terms
3) -30x + 30 + 5x
Solve
4) 5v + 5(-6v + 6) = -6(4v – 4)

3. 5v + 5(-6v + 6) = -6(4v – 4)

4. Essential Questions:
What is an inequality?
 How can I graph solutions
of equations and inequalities
on a number line?

5. Let’s Graph the Solution to an
equation on a Number Line!
Number lines are used to graph some solutions.
x + 3 = -1
We already found the x + 3 -3 = -1 -3
solution to this equation. x=-4
Now, what does it mean on a number line?

6. If we say that “a variable = a number”, that
is where we place the point on the
number line!
Example: X = -3
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6

7. What Is The Difference Between
Equalities And Inequalities?
The only difference is the number
of solutions!
•An equality gives one definite solution.
•An inequality give a set of solutions!

8. Inequality Symbols
< Less Than x<5
> Greater Than x>5
< Less Than OR Equal to x<5
> Greater Than OR Equal to x>5

9. If we say that x > 6,
aren’t we stating that x can be
any amount greater than 6?
What are some examples??

10. How Do We View A Set Of
Solutions On A Number Line?
Let’s find out!

11. When graphing inequalities, we must show where
to begin the set of solutions and where they
continue on the number line.
For example:
r < 1
Use an
open dot
-2 -1 0 1 2

12. When graphing inequalities, we must show where
to begin the set of solutions and where they
continue on the number line.
For example:
r > 1
Use a
closed dot
-2 -1 0 1 2

13. If you noticed,
some number lines had filled in circles
and others did not.
What do you think was the reason?

14. The filled in circle shows that the
designated number is
included in the solution set.
This is shown with < or >.
X < -4

15. The unfilled circle shows that the
designated number is not
included in the solution set.
This is shown with < or >.
X < -4

16. Inequality Symbols
< Less Than – Open Dot
> Greater Than – Open Dot
< Less Than OR Equal to – Closed Dot
> Greater Than OR Equal to – Closed Dot

17. Solve and Graph the Following on Your
Paper:
A.) x – 1 > 5
B.) 4 + n < -1
C.) 5+ z > 10
D.) -15 + r < -14

18. You should have drawn these solutions:
A.) x - 1 > 5
-5 -4 -3 -2 -1 0 1 2 3 4 5 6
B.) 4 + n < -1
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6
C.) 5 + z > 10
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6
D.) -15 + r < -14
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5

19. On your paper, solve and graph
the following:
A. 5 + n = 9
B. 19 + m > 5
C. -6 + b = 4
D. K - 17 < 14
E. 2d > 12

20. Now, Let’s Compare Equalities
and Inequalities:
Equalities Inequalities
Solve by performing Solve by performing
the inverse operation the inverse operation
Only one definite A set of solutions
solution The solution is shown
The solution is shown with a filled or unfilled
with one filled circle on circle with a line or line
a number line segment

21. One more difference…

When you
multiply
When you
OR
multiply
Divide
OR
BY
Divide
A Positive
BY
the inequality
A negative
stays the same
flip
the inequality

22. Vocabulary
•Number line
•Solution
•Inverse Operation
•Equality
•Inequality

23. Remember:
Perform the
inverse operation
to solve for a variable!