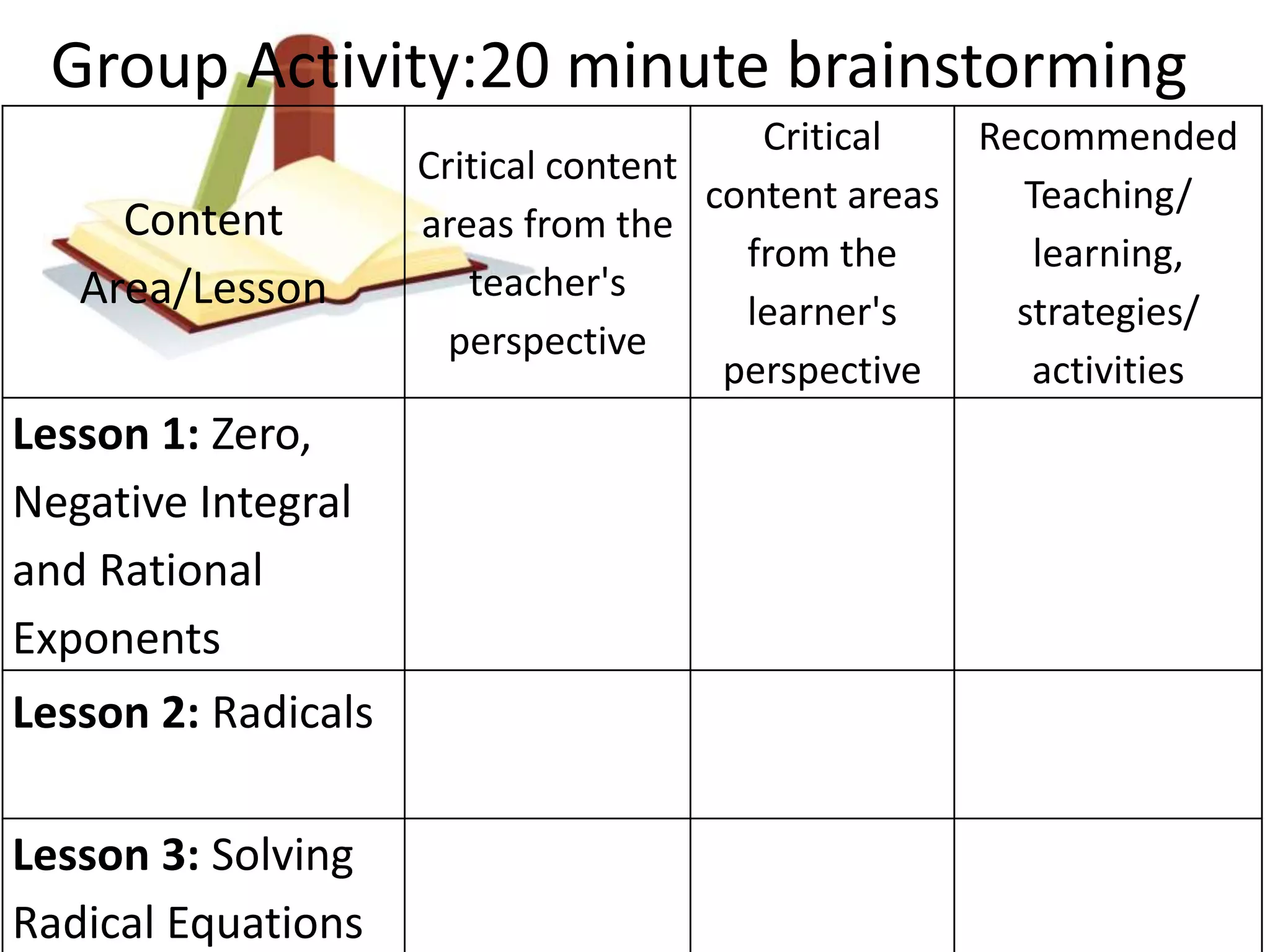
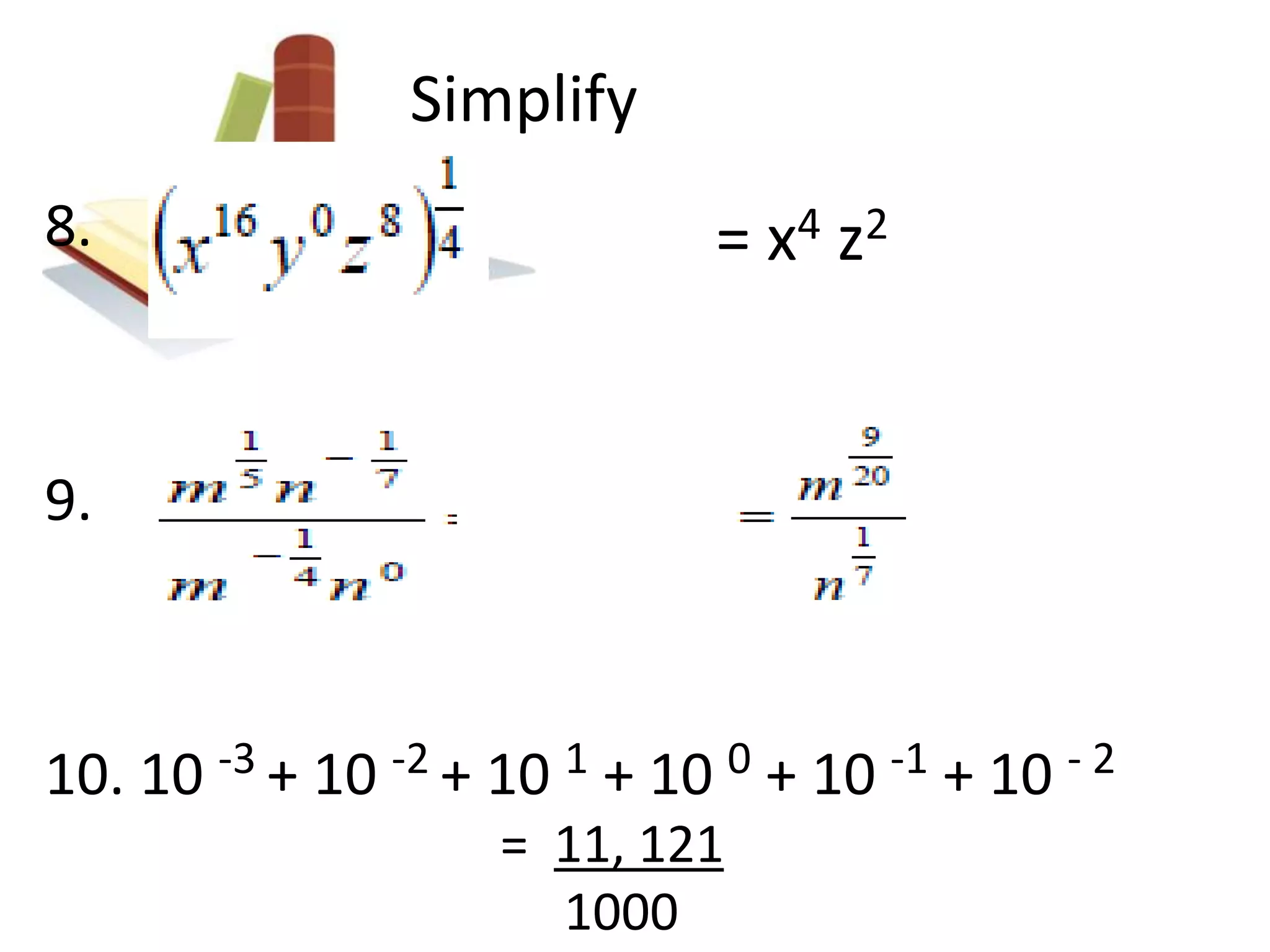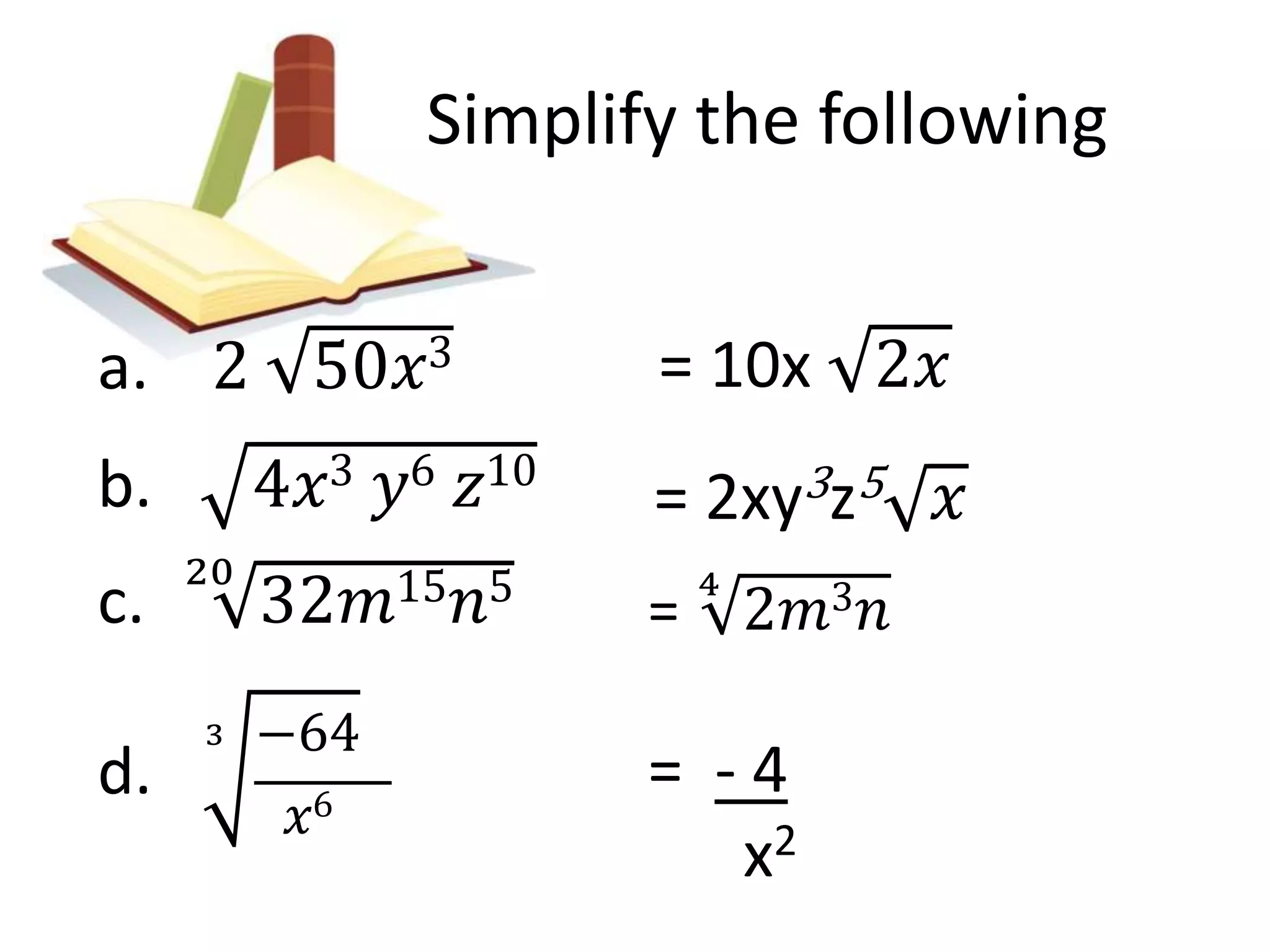This document summarizes a module on rational exponents and radicals that was presented at a 2014 mid-year inset for secondary mathematics teachers. The module covered lessons on zero, negative integral and rational exponents, radicals, and solving radical equations. It provided examples of simplifying expressions using laws of exponents and radicals. Recommended teaching strategies included problem-solving activities and a group brainstorming activity to discuss critical content areas and difficulties from teacher and student perspectives.

1. 2014 DIVISION MID-YEAR INSET ON
CONTENT AND PEDAGOGY FOR
SECONDARY MATHEMATICS
EDUCATION
DAYAP NATIONAL HIGH SCHOOL
CALAUAN, LAGUNA
ALVIN O. INSORIO
Pacita Complex National High School

2. Module 4
Rational
Exponents and
Radicals

3. Lessons: 1. Zero, Negative Integral
and Rational Exponents
2. Radicals
3. Solving Radical Equations

4. Priming
1. Have you ever wondered about how to
identify the side lengths of a square lot
if you know its area?
2. Have you tried solving for the length of
any side of a right triangle?
3. Has it come to your mind how you can
find the radius of a cylindrical water
tank given its volume?

5. Recall: Laws of Exponents
= 1, if m= n
Zero Exponent
a0 = 1
Negative Exponent
a−푚 = 1/a푚
1
a − 푚 = a푚

6. Drill
Simplify using laws of exponents
1) 3x0
2) ( - 3x ) 0
3) ( 3x 3m y 2n ) 3
4) ( 2x y z -3 ) ( - 4x 3y z5 )
5) (2m ½)( - 3m 2/3 )
6) 3 2 . 4 0 + 1 ½ . 5 0
7) 64 . 81
27 . 216
= 3
= 1
= 27x 9m y 6n
= - 8x 4y z 2
= - 6m 7/6
= 10
= 8/9

7. Simplify
8.
9.
= x4 z2
10. 10 -3 + 10 -2 + 10 1 + 10 0 + 10 -1 + 10 - 2
= 11, 121
1000

8. Radical Expression
A radical expression or radical is an
expression containing the symbol
which is called radical sign. In symbols
푛 푎푚 , n is called index or order and am is
called the radicand.

9. Change the following into
radical form
1. 5x ½
2. ( 3 mn2 ) 2/3
3. ( 2n2 ) ¾
4. ( x2 + 3 ) 1/3
( x2 – 3 ) – 1/3
= 5 푥
= 3 9푚 2 푛 4
=
4 8푛6
=

10. Change the following into
exponential form
1. 3 2푥3
2.
3.
= 3 ( 2x3 ) 1/2
=
= (4r2 s3 t4 ) 2/5

11. Laws of Radicals
The simplified form of radical expression would
require;
• No prime factors of a radicand has an exponent
equal or greater than the index.
• No radicand contains a fraction
• No denominator contains a radical sign.

12. Simplify the following
a. 2 50푥3
b. 4푥3 푦6 푧10
c. 20 32푚15푛5
d.
3 −64
푥6
= 10x 2푥
= 2xy3z5 푥
= 4 2푚3푛
= - 4
x2

13. Addition and subtraction
of radicals
We add or subtract by combining the similar/like
radicals
1. 5 6 + 9 6 − 8 6
2. 20 3 푥 −10 4 푥 + 4 푥 − 53 푥
3. 2 27 + 3 48 − 4 12
= 6 6
=153 푥 − 94 푥
= 10 3

14. Multiplication of radicals
= 42
= 5 + 3 5
= 6 108푥5
1.
2. ( 2 + 5 ) ( 5 - 5 )
3.

15. Division of radicals
= 3 4/3
= 3 3 + 3 2
= 2 6 243
1. 43 2 ÷ 63 4
2. 3 ÷ ( 3 − 2 )
3. 63 3 ÷ 3

16. Radical Equation
It is an equation in which the variable
appears in a radicand.
Solve for x
1. x – 6 = 푥
2. 4 + 푥 − 2 = x
3. 3 3 푥 + 1 = 2
= 9 is the only solution
4 is extraneous root
= 6 is the only solution
3 is extraneous root
= - 19/27

17. Problem Solving
A woman walks 5 meters to the east
going to school and then walks 9 meters
northward going to the church. How far is
she from the starting point which is her
house? Express your answer in radical
form.
Answer: 106

18. Group Activity:20 minute brainstorming
Content
Area/Lesson
Critical content
areas from the
teacher's
perspective
Critical
content areas
from the
learner's
perspective
Recommended
Teaching/
learning,
strategies/
activities
Lesson 1: Zero,
Negative Integral
and Rational
Exponents
Lesson 2: Radicals
Lesson 3: Solving
Radical Equations

19. Analysis
1. From the activity, what are the content areas
teachers do find most easy to teach? most difficult to
teach?
2. What are the common difficulties encountered by
the teachers in teaching the concepts of rational
exponents and radicals?
3. Which of the content/s is/are most challenging for
the students to learn? most difficult to comprehend?
4. What are the insights you have gained from this
activity?
5. Are the recommended strategies/activities practical
and appropriate in eliminating the perceived
difficulty?

20. Abstraction
1. Explain the identified critical content areas
based on the perception and prior
experience of the teachers and the learners.
2. Discuss appropriate teaching strategies and
learning activities that can be used in the
classroom.
3. Share best practices in teaching variations.

21. Application
1. Create a scenario of the task in
paragraph form about variation
incorporating GRASPS format. Create a
rubric for the grading of this activity.
2. Present the output to the class.

22. THANK YOU!!!!
GOD BLESS US ALL