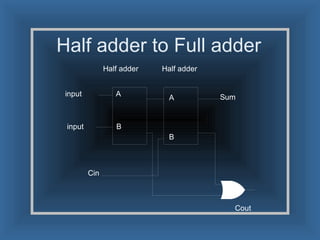
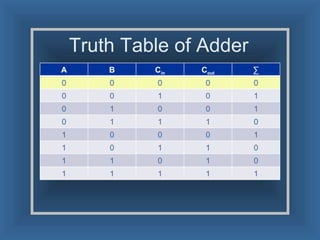
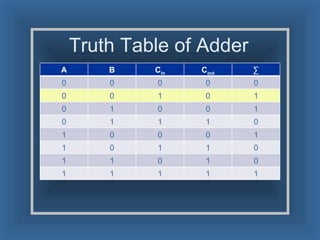
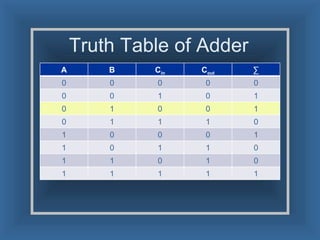
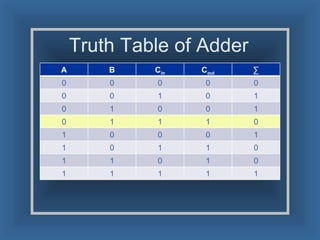
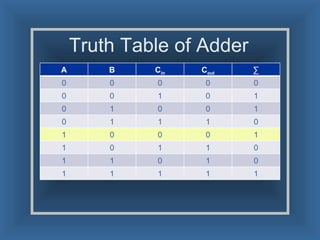
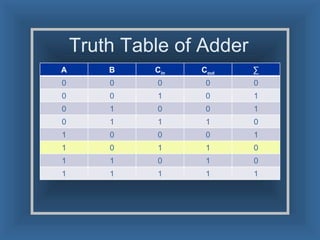
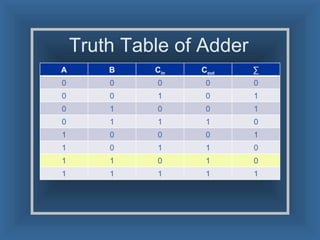
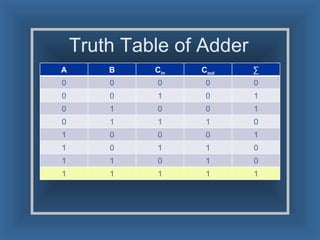
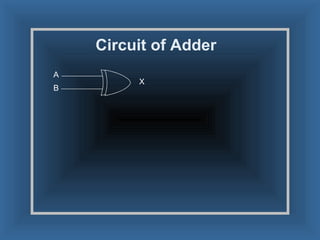
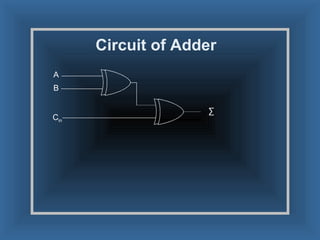
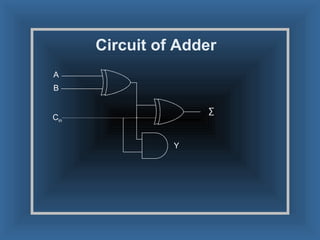
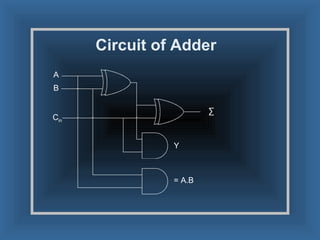
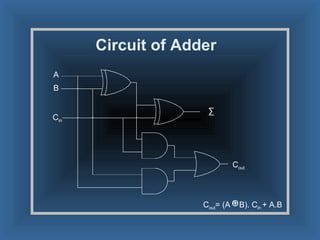
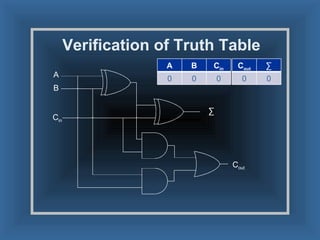
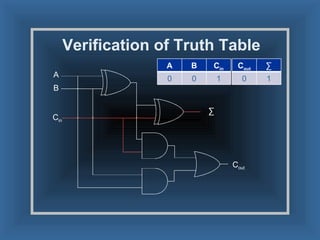
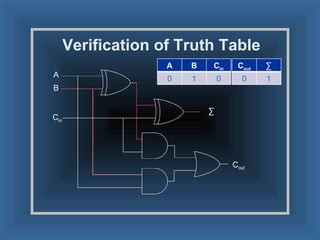
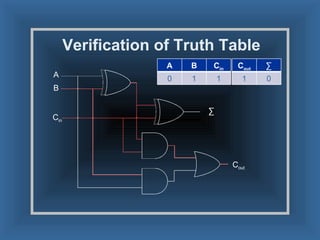
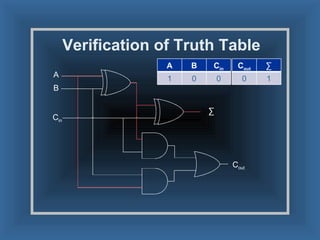
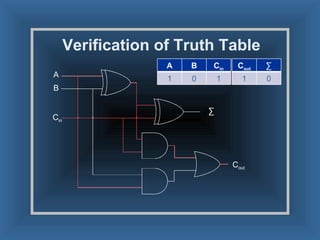
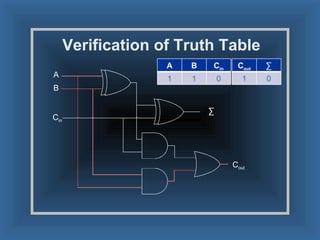
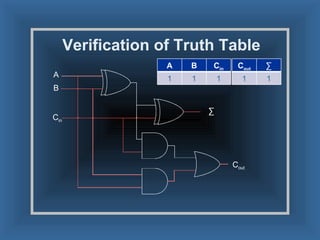
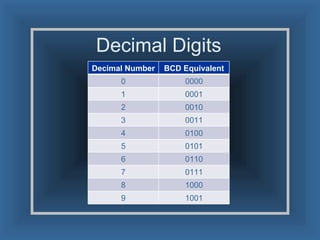
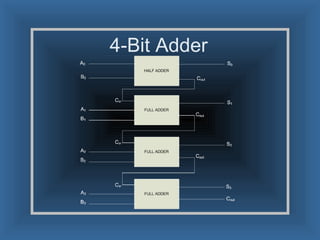
An adder is a digital circuit that performs addition of numbers. There are two main types: a half adder that adds two bits and produces a sum and carry bit, and a full adder that adds two bits and a carry bit to produce a sum and carry out bit. Adders are used in arithmetic logic units to perform arithmetic operations and are important in many digital systems that process numeric data.

1. Basic Adders +

2. What is Adder?

3. Adder : In electronics an adder is digital circuit that perform addition of numbers. In modern computer adder reside in the arithmetic logic unit (ALU).

4. Adders : Adders are important not only in the computer but also in many types of digital systems in which the numeric data are processed. Types of adder: Half adder Full adder

5. Half adder : The half adder accepts two binary digits on its inputs and produce two binary digits outputs, a sum bit and a carry bit.

6. Full adder : The full adder accepts two inputs bits and an input carry and generates a sum output and an output carry.

7. Half adder to Full adder

8. Truth Table of Adder

9. Truth Table of Adder A B C in C out ∑ 0 0 0 0 0 0 0 1 0 1 0 1 0 0 1 0 1 1 1 0 1 0 0 0 1 1 0 1 1 0 1 1 0 1 0 1 1 1 1 1

10. Truth Table of Adder A B C in C out ∑ 0 0 0 0 0 0 0 1 0 1 0 1 0 0 1 0 1 1 1 0 1 0 0 0 1 1 0 1 1 0 1 1 0 1 0 1 1 1 1 1

11. Truth Table of Adder A B C in C out ∑ 0 0 0 0 0 0 0 1 0 1 0 1 0 0 1 0 1 1 1 0 1 0 0 0 1 1 0 1 1 0 1 1 0 1 0 1 1 1 1 1

12. Truth Table of Adder A B C in C out ∑ 0 0 0 0 0 0 0 1 0 1 0 1 0 0 1 0 1 1 1 0 1 0 0 0 1 1 0 1 1 0 1 1 0 1 0 1 1 1 1 1

13. Truth Table of Adder A B C in C out ∑ 0 0 0 0 0 0 0 1 0 1 0 1 0 0 1 0 1 1 1 0 1 0 0 0 1 1 0 1 1 0 1 1 0 1 0 1 1 1 1 1

14. Truth Table of Adder A B C in C out ∑ 0 0 0 0 0 0 0 1 0 1 0 1 0 0 1 0 1 1 1 0 1 0 0 0 1 1 0 1 1 0 1 1 0 1 0 1 1 1 1 1

15. Truth Table of Adder A B C in C out ∑ 0 0 0 0 0 0 0 1 0 1 0 1 0 0 1 0 1 1 1 0 1 0 0 0 1 1 0 1 1 0 1 1 0 1 0 1 1 1 1 1

16. Truth Table of Adder A B C in C out ∑ 0 0 0 0 0 0 0 1 0 1 0 1 0 0 1 0 1 1 1 0 1 0 0 0 1 1 0 1 1 0 1 1 0 1 0 1 1 1 1 1

17. Circuit of Adder A B

18. Circuit of Adder A B X

19. Circuit of Adder A B C in ∑

20. Circuit of Adder A B C in ∑ Y

21. Circuit of Adder A B C in ∑ = A.B Y

22. Circuit of Adder A B C in ∑ C out C out = (A B). C in + A.B

23. Verification of Truth Table A B C in ∑ C out A B C in 0 0 0 C out ∑ 0 0

24. Verification of Truth Table A B C in ∑ C out A B C in 0 0 1 C out ∑ 0 1

25. Verification of Truth Table A B C in ∑ C out A B C in 0 1 0 C out ∑ 0 1

26. Verification of Truth Table A B C in ∑ C out A B C in 0 1 1 C out ∑ 1 0

27. Verification of Truth Table A B C in ∑ C out A B C in 1 0 0 C out ∑ 0 1

28. Verification of Truth Table A B C in ∑ C out A B C in 1 0 1 C out ∑ 1 0

29. Verification of Truth Table A B C in ∑ C out A B C in 1 1 0 C out ∑ 1 0

30. Verification of Truth Table A B C in ∑ C out A B C in 1 1 1 C out ∑ 1 1

31. Applications of Adder THE BCD ADDER

32. BCD Adder Binary Coded Decimal Adder Just adds decimal digits

33. Binary Coded Decimal It is possible to represent decimal numbers simply by encoding each decimal digit in binary form called binary coded decimal Because there are 10 digits to represent, it is necessary to use four bits per digit. From 0=0000 to 9=1001 by using 8421 code. For example: Convert 98 into BCD. 9 8 1001 1000 BCD representation was used in some early computers and many handheld calculators.

34. Decimal Digits Decimal Number BCD Equivalent 0 0000 1 0001 2 0010 3 0011 4 0100 5 0101 6 0110 7 0111 8 1000 9 1001

35. The BCD Adder BCD is a numerical code and can be used in arithmetic operations. Addition is the most important operation in BCD. Following are the steps to perform addition: Step1 Add the two BCD numbers, using the rules for binary addition. Step2 If a 4-bit sum is equal to or less than 9, it is a valid BCD number.

36. THE BCD ADDER Add the following BCD number 0011 + 0100 0011 3 + 0100 + 4 0111 7

37. 4-Bit Adder A single full –adder is capable of adding two 1-bit numbers and input carry. What happens if we want to add binary numbers with more than 1-bit? The concept of additional full-adders must be used i.e. to add 2-bit numbers two adders must be needed and to add 4-bit numbers four adders must be needed.

38. 4-Bit Adder

39. Thanks!