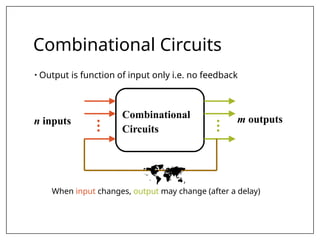
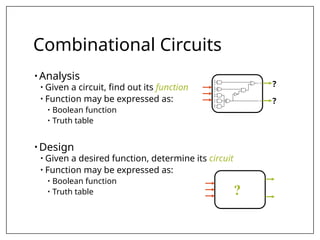
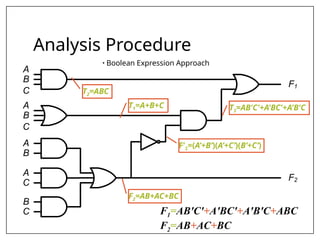
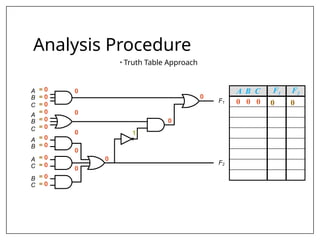
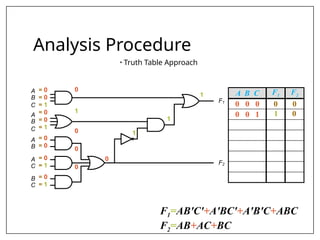
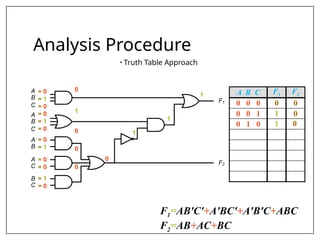
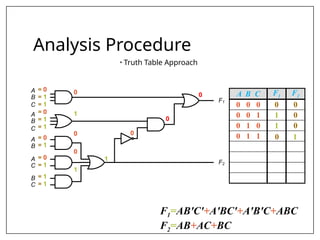
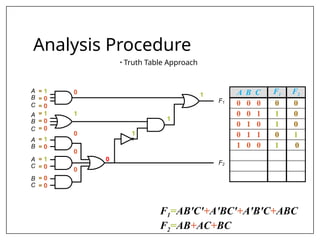
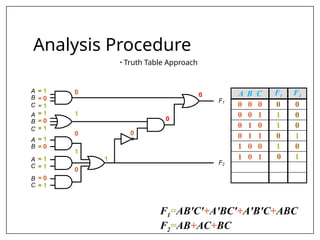
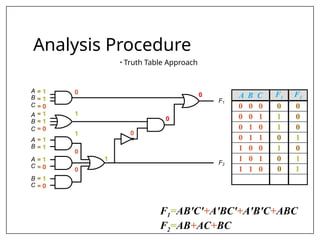
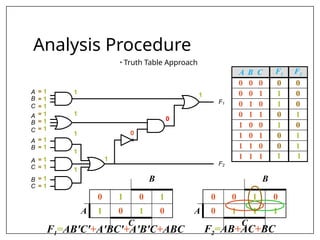
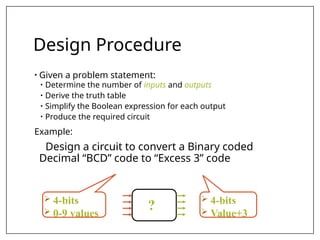
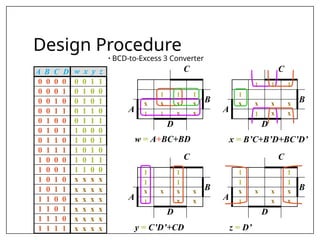
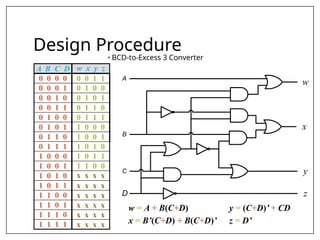
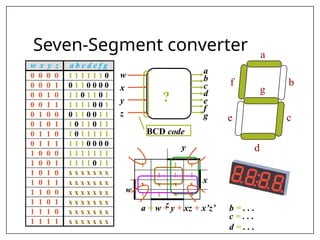
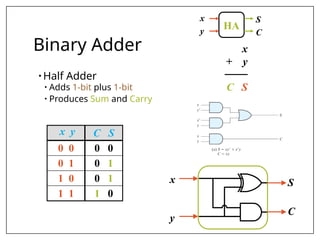
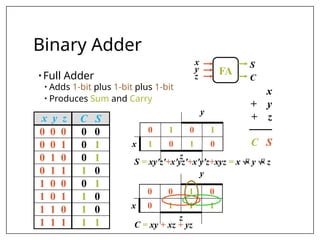
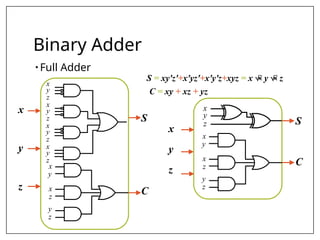
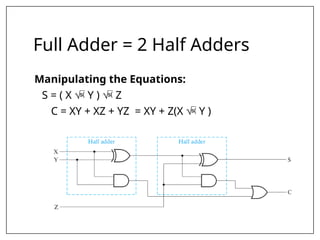
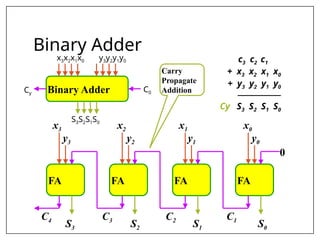
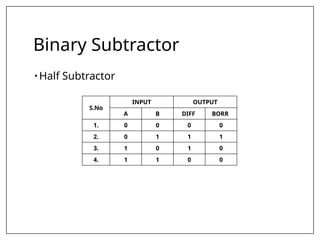
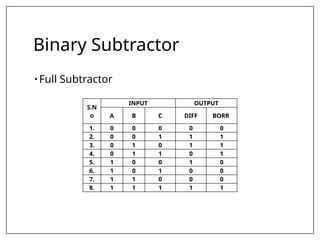
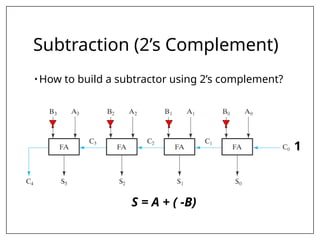
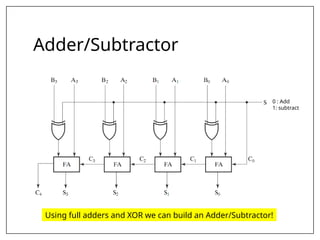
This document covers combinational and sequential circuit design, focusing on combinational circuits that use logic gates where outputs depend solely on inputs without feedback. It details analysis and design procedures, including the use of truth tables and boolean expressions, as well as examples such as BCD to excess-3 converters and binary adders and subtractors. The document also describes classifications of combinational logic functions such as arithmetic operations and code converters.

1. LOGIC AND SEQUENTIAL CIRCUIT
DESIGN
SPRING 2024

2. CHAPTER 4 – COMBINATIONAL LOGIC
2

3. Combinational Circuits
• Two classes of logic circuits:
• Combinational Circuits
• Sequential Circuits
• A Combinational circuit consists of logic gates
• Output depends only on input
• A Sequential circuit consists of logic gates and
memory
• Output depends on current inputs and previous ones
(stored in memory)
• Memory defines the state of the circuit.

4. Combinational Circuits
• Output is function of input only i.e. no feedback
When input changes, output may change (after a delay)
•
•
•
•
•
•
n inputs m outputs
Combinational
Circuits


5. Classification of Combinational
Logic
• Arithmetic & logical functions (adder, subtractor,
comparator)
• Data transmission(decoder, encoder, multiplexer,
de-multiplexer)
• Code converters( BCD, grey code,7-segment)

6. Combinational Circuits
• Analysis
• Given a circuit, find out its function
• Function may be expressed as:
• Boolean function
• Truth table
• Design
• Given a desired function, determine its circuit
• Function may be expressed as:
• Boolean function
• Truth table
C
B
A
C
B
A
B
A
C
A
C
B
F1
F2
?
?
?

7. Analysis Procedure
• Boolean Expression Approach
C
B
A
C
B
A
B
A
C
A
C
B
F1
F2
T2=ABC
T1=A+B+C
F2=AB+AC+BC
F’2=(A’+B’)(A’+C’)(B’+C’)
T3=AB'C'+A'BC'+A'B'C
F1=AB'C'+A'BC'+A'B'C+ABC
F2=AB+AC+BC

8. C
B
A
C
B
A
B
A
C
A
C
B
F1
F2
Analysis Procedure
• Truth Table Approach
A B C F1 F2
0 0 0
= 0
= 0
= 0
= 0
= 0
= 0
= 0
= 0
= 0
= 0
= 0
= 0
0
0
0
0
0
0
1
0
0
0 0

9. C
B
A
C
B
A
B
A
C
A
C
B
F1
F2
Analysis Procedure
• Truth Table Approach
0
1
= 0
= 0
= 1
= 0
= 0
= 1
= 0
= 0
= 0
= 1
= 0
= 1
0
1
0
0
0
A B C F1 F2
0 0 0 0 0
0 0 1 1 0
1
1
F1=AB'C'+A'BC'+A'B'C+ABC
F2=AB+AC+BC

10. C
B
A
C
B
A
B
A
C
A
C
B
F1
F2
Analysis Procedure
• Truth Table Approach
0
1
0
1
0
0
0
1
1 A B C F1 F2
0 0 0 0 0
0 0 1 1 0
0 1 0 1 0
= 0
= 1
= 0
= 0
= 1
= 0
= 0
= 1
= 0
= 0
= 1
= 0
F1=AB'C'+A'BC'+A'B'C+ABC
F2=AB+AC+BC

11. C
B
A
C
B
A
B
A
C
A
C
B
F1
F2
Analysis Procedure
• Truth Table Approach
0
0
0 A B C F1 F2
0 0 0 0 0
0 0 1 1 0
0 1 0 1 0
0 1 1 0 1
= 0
= 1
= 1
= 0
= 1
= 1
= 0
= 1
= 0
= 1
= 1
= 1
0
1
0
0
1
1
F1=AB'C'+A'BC'+A'B'C+ABC
F2=AB+AC+BC

12. C
B
A
C
B
A
B
A
C
A
C
B
F1
F2
Analysis Procedure
• Truth Table Approach
1
1
1
0
A B C F1 F2
0 0 0 0 0
0 0 1 1 0
0 1 0 1 0
0 1 1 0 1
1 0 0 1 0
= 1
= 0
= 0
= 1
= 0
= 0
= 1
= 0
= 1
= 0
= 0
= 0
0
1
0
0
0
F1=AB'C'+A'BC'+A'B'C+ABC
F2=AB+AC+BC

13. C
B
A
C
B
A
B
A
C
A
C
B
F1
F2
Analysis Procedure
• Truth Table Approach
= 1
= 0
= 1
= 1
= 0
= 1
= 1
= 0
= 1
= 1
= 0
= 1
0
1
0
1
0
0
0
0
1
A B C F1 F2
0 0 0 0 0
0 0 1 1 0
0 1 0 1 0
0 1 1 0 1
1 0 0 1 0
1 0 1 0 1
F1=AB'C'+A'BC'+A'B'C+ABC
F2=AB+AC+BC

14. C
B
A
C
B
A
B
A
C
A
C
B
F1
F2
Analysis Procedure
• Truth Table Approach
0
0
0
1
0 1
= 1
= 1
= 0
= 1
= 1
= 0
= 1
= 1
= 1
= 0
= 1
= 0
0
1
1
0
0
A B C F1 F2
0 0 0 0 0
0 0 1 1 0
0 1 0 1 0
0 1 1 0 1
1 0 0 1 0
1 0 1 0 1
1 1 0
F1=AB'C'+A'BC'+A'B'C+ABC
F2=AB+AC+BC

15. C
B
A
C
B
A
B
A
C
A
C
B
F1
F2
Analysis Procedure
• Truth Table Approach
0
0
1
1
= 1
= 1
= 1
= 1
= 1
= 1
= 1
= 1
= 1
= 1
= 1
= 1
1
1
1
1
1
A B C F1 F2
0 0 0 0 0
0 0 1 1 0
0 1 0 1 0
0 1 1 0 1
1 0 0 1 0
1 0 1 0 1
1 1 0 0 1
1 1 1 1 1
B
0 1 0 1
A 1 0 1 0
C
B
0 0 1 0
A 0 1 1 1
C
F1=AB'C'+A'BC'+A'B'C+ABC F2=AB+AC+BC

16. Design Procedure
• Given a problem statement:
• Determine the number of inputs and outputs
• Derive the truth table
• Simplify the Boolean expression for each output
• Produce the required circuit
Example:
Design a circuit to convert a Binary coded
Decimal “BCD” code to “Excess 3” code
 4-bits
 0-9 values
 4-bits
 Value+3
?

17. Design Procedure
• BCD-to-Excess 3 Converter
A B C D w x y z
0 0 0 0 0 0 1 1
0 0 0 1 0 1 0 0
0 0 1 0 0 1 0 1
0 0 1 1 0 1 1 0
0 1 0 0 0 1 1 1
0 1 0 1 1 0 0 0
0 1 1 0 1 0 0 1
0 1 1 1 1 0 1 0
1 0 0 0 1 0 1 1
1 0 0 1 1 1 0 0
1 0 1 0 x x x x
1 0 1 1 x x x x
1 1 0 0 x x x x
1 1 0 1 x x x x
1 1 1 0 x x x x
1 1 1 1 x x x x
C
1 1 1
B
A
x x x x
1 1 x x
D
C
1 1 1
1
B
A
x x x x
1 x x
D
C
1 1
1 1
B
A
x x x x
1 x x
D
C
1 1
1 1
B
A
x x x x
1 x x
D
w = A+BC+BD x = B’C+B’D+BC’D’
y = C’D’+CD z = D’

18. Design Procedure
• BCD-to-Excess 3 Converter
A B C D w x y z
0 0 0 0 0 0 1 1
0 0 0 1 0 1 0 0
0 0 1 0 0 1 0 1
0 0 1 1 0 1 1 0
0 1 0 0 0 1 1 1
0 1 0 1 1 0 0 0
0 1 1 0 1 0 0 1
0 1 1 1 1 0 1 0
1 0 0 0 1 0 1 1
1 0 0 1 1 1 0 0
1 0 1 0 x x x x
1 0 1 1 x x x x
1 1 0 0 x x x x
1 1 0 1 x x x x
1 1 1 0 x x x x
1 1 1 1 x x x x
w
x
D
C
z
y
B
A
w = A + B(C+D)
x = B’(C+D) + B(C+D)’
y = (C+D)’ + CD
z = D’

19. Seven-Segment converter
• Seven-Segment Display
• A seven-segment display is digital readout found
in electronic devices like clocks, TVs, etc.
• Made of seven light-emitting diodes (LED) segments;
each segment is controlled separately.

20. Seven-Segment converter a
b
c
g
e
d
f
?
w
x
y
z
a
b
c
d
e
f
g
w x y z a b c d e f g
0 0 0 0 1 1 1 1 1 1 0
0 0 0 1 0 1 1 0 0 0 0
0 0 1 0 1 1 0 1 1 0 1
0 0 1 1 1 1 1 1 0 0 1
0 1 0 0 0 1 1 0 0 1 1
0 1 0 1 1 0 1 1 0 1 1
0 1 1 0 1 0 1 1 1 1 1
0 1 1 1 1 1 1 0 0 0 0
1 0 0 0 1 1 1 1 1 1 1
1 0 0 1 1 1 1 1 0 1 1
1 0 1 0 x x x x x x x
1 0 1 1 x x x x x x x
1 1 0 0 x x x x x x x
1 1 0 1 x x x x x x x
1 1 1 0 x x x x x x x
1 1 1 1 x x x x x x x
y
1 1 1
1 1 1
x
w
x x x x
1 1 x x
z
BCD code
a = w + y + xz + x’z’ b = . . .
c = . . .
d = . . .

21. Binary Adder
• Half Adder
• Adds 1-bit plus 1-bit
• Produces Sum and Carry
HA
x
y
S
C
x y C S
0 0 0 0
0 1 0 1
1 0 0 1
1 1 1 0
x
+ y
───
C S
x
y
S
C

22. Binary Adder
• Full Adder
• Adds 1-bit plus 1-bit plus 1-bit
• Produces Sum and Carry
x y z C S
0 0 0 0 0
0 0 1 0 1
0 1 0 0 1
0 1 1 1 0
1 0 0 0 1
1 0 1 1 0
1 1 0 1 0
1 1 1 1 1
x
+ y
+ z
───
C S
FA
x
y
z
S
C
y
0 1 0 1
x 1 0 1 0
z
y
0 0 1 0
x 0 1 1 1
z
S = xy'z'+x'yz'+x'y'z+xyz = x  y  z
C = xy + xz + yz

23. Binary Adder
• Full Adder
x
y
z
S
C
x
y
x
z
y
z
x
y
z
x
y
z
x
y
z
x
y
z
x
y
z
x
y
z
x
y
x
z
y
z
S
C
S = xy'z'+x'yz'+x'y'z+xyz = x  y  z
C = xy + xz + yz

24. Full Adder = 2 Half Adders
Manipulating the Equations:
S = ( X  Y )  Z
C = XY + XZ + YZ = XY + Z(X  Y )

25. Full Adder – for using Half-
adders
Manipulating the Equations:
S = ( X  Y )  Z
C = XY + XZ + YZ
= XY + XYZ + XY’Z + X’YZ + XYZ
= XY + XYZ + XY’Z + X’YZ
= XY( 1 + Z) + Z(XY’ + X’Y)
= XY + Z(X  Y )

26. Binary Adder
c3 c2 c1 .
+ x3 x2 x1 x0
+ y3 y2 y1 y0
────────
Cy S3 S2 S1 S0
FA
x3 x2 x1 x0
FA
FA
FA
y3 y2 y1 y0
S3 S2 S1 S0
C4 C3 C2 C1
0
Binary Adder
x3x2x1x0 y3y2y1y0
S3S2S1S0
C0
Cy
Carry
Propagate
Addition

27. Bigger Adders
• How to build an adder for n-bit numbers?
• Example: 4-Bit Adder
• Inputs ?
• Outputs ?
• What is the size of the truth table?
• How many functions to optimize?

28. Bigger Adders
• How to build an adder for n-bit numbers?
• Example: 4-Bit Adder
• Inputs ? 9 inputs
• Outputs ? 5 outputs
• What is the size of the truth table? 512 rows! ()
• How many functions to optimize? 5 functions (S+ Last Carry)

29. Binary Adder
1 0 0 0
0 1 0 1
+ 0 1 1 0
1 0 1 1
• To add n-bit numbers:
• Use n Full-Adders in Cascade.
• The carries propagates as in addition by hand.
Carry in
This adder is called ripple carry adder

30. Binary Subtractor
• Half Subtractor
A logic circuit which is used for subtracting one
single bit binary number from another single bit
binary number is called half subtractor.

31. Binary Subtractor
• Half Subtractor
S.No
INPUT OUTPUT
A B DIFF BORR
1. 0 0 0 0
2. 0 1 1 1
3. 1 0 1 0
4. 1 1 0 0

32. Binary Subtractor
• Full Subtractor
The Full subtractor is a combinational circuit
which is used to perform subtraction of three
bits.

33. Binary Subtractor
• Full Subtractor
S.N
o
INPUT OUTPUT
A B C DIFF BORR
1. 0 0 0 0 0
2. 0 0 1 1 1
3. 0 1 0 1 1
4. 0 1 1 0 1
5. 1 0 0 1 0
6. 1 0 1 0 0
7. 1 1 0 0 0
8. 1 1 1 1 1

34. Binary Subtractor (Your
Practice)
• Derive simplified Boolean expressions for Half
Subtractor and Full Subtractor.

35. Subtraction (2’s Complement)
• How to build a subtractor using 2’s complement?

36. Subtraction (2’s Complement)
• How to build a subtractor using 2’s complement?
1
S = A + ( -B)

37. Adder/Subtractor
• How to build a circuit that performs both
addition and subtraction?

38. Adder/Subtractor
Using full adders and XOR we can build an Adder/Subtractor!
0 : Add
1: subtract