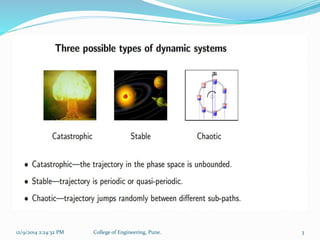
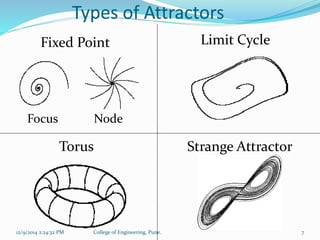
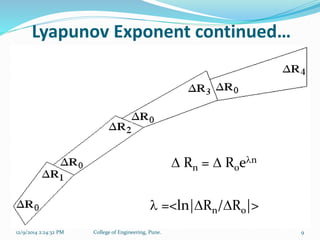
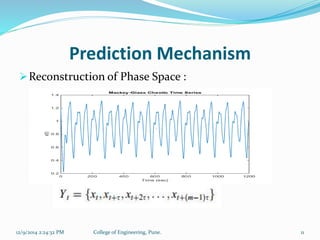
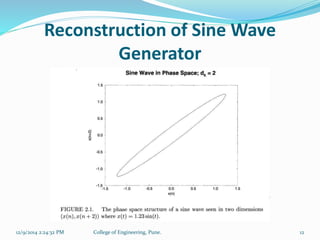
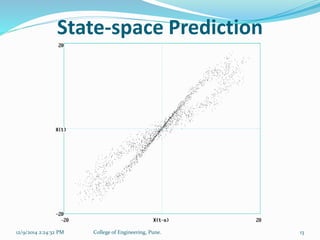
The document discusses time series and dynamical systems, focusing primarily on chaos theory and its applications. It outlines concepts such as attractors, Lyapunov exponents, and Takens' theorem, explaining their significance in predicting the behavior of chaotic systems. Additionally, it provides a prediction mechanism and algorithm for reconstructing phase space from time series data.

1. - By Mr. Suhel S. Mulla
SY M. Tech (Digital System).
MIS No. – 121333009.
College of Engineering, Pune.

2. Time Series :
A time series a sequence of data points, typically consisting
of successive measurements made over a time interval.
e.g. ocean tides, counts of sunspots, and the daily closing
value of the Dow Jones Industrial Average.
Dynamical System :
A dynamical system is a concept in mathematics where a
fixed rule describes how a point in a geometrical space
depends on time.
e.g. Mathematical models that describe the swinging of a
clock pendulum, the flow of water in a pipe, and the
number of fish each springtime in a lake.
12/9/2014 2:24:32 PM College of Engineering, Pune. 2

3. 12/9/2014 2:24:32 PM College of Engineering, Pune. 3

4. What is Chaos…??
In common usage, chaos means “a state of disorder”
 Difference between chaotic and random signal.
Chaos theory studies behavior of dynamical systems
which are sensitive to initial conditions.
Chaotic system can be analog or digital. In analog
chaos, it is given by differential equation while in
digital case, it is given by difference equation
Chaotic systems are predictable for a while, then they
appear to become random.
12/9/2014 2:24:32 PM College of Engineering, Pune. 4

5. Continued……
 In Lorenz words :
“Chaos is when present determines future, but
approximate present determines approximate future.”
 The approximate present information comes from even
minute errors in measurement which are inevitable.
Thus, correct measurement of chaotic system is not
possible.
 This makes the system forecast possible for small period of
time.
 The term used for prediction interval of chaotic system is
called as Lyapunov Exponent.
12/9/2014 2:24:32 PM College of Engineering, Pune. 5

6. Attractors
An attractor is a set of numerical properties toward
which a system tends to evolve, for a wide variety of
starting conditions of the system.
Types –
1. Fixed Point
2. Limit Cycle
3. Limit Torous
4. Strange Attractor.
12/9/2014 2:24:32 PM College of Engineering, Pune. 6

7. Types of Attractors
Fixed Point Limit Cycle
Focus Node
Torus Strange Attractor
12/9/2014 2:24:32 PM College of Engineering, Pune. 7

8. Lyapunov Exponent
 It is a quantity that characterizes the rate of
separation of infinitesimally close trajectories.
Quantitatively, two trajectories in phase space with
initial separation δZ0 diverge at a rate given by
where λ is the Lyapunov exponent.
It determines a notion of predictability for a
dynamical system.
For the chaotic system it has to be between 0 and 1.
12/9/2014 2:24:32 PM College of Engineering, Pune. 8

9. Lyapunov Exponent continued…
 Rn =  R0en
 =<ln|Rn/R0|>
12/9/2014 2:24:32 PM College of Engineering, Pune. 9

10. Takens Theorem
 It gives a notion through which complete system can be
reconstructed from the observed time series.
 The key point is that, though we are observing only one
time series, it is made by all the state variables present in
the system.
 Thus, the history of time series can determine the nature of
all the state variables in the system.
 According to Taken’s theorem, an m-dimensional
system requires (2m+1) delay co-ordinated graph of
observed time series.
 It tells us that we do not have to measure all the state space
variables of the system for finding out the internal details
of the system.
12/9/2014 2:24:32 PM College of Engineering, Pune. 10

11. Prediction Mechanism
Reconstruction of Phase Space :
12/9/2014 2:24:32 PM College of Engineering, Pune. 11

12. Reconstruction of Sine Wave
Generator
12/9/2014 2:24:32 PM College of Engineering, Pune. 12

13. State-space Prediction
12/9/2014 2:24:32 PM College of Engineering, Pune. 13

14. Determination of Delay time ‘τ’
Delay time can be calculated by finding
autocorrelation function of the data and selecting ‘τ’
as its first zero crossing.
 Small value of ‘τ’ gives the reconstructed delay
graph approximately linear whereas large value of
‘τ’ gives completely uncorrelated graph.
 Along with all the methods, ‘τ’ can also be calculated
by trial and error method, such results give satisfactory
answers in some cases.
12/9/2014 2:24:32 PM College of Engineering, Pune. 14

15. Embedding Dimensions ‘d’
 If the co-ordinated graph has less dimensions
provided by Taken’s theorem, then the orbits overlap
and a complex path crisis is created.
 Sometimes the reconstructed graph with less
dimensions than required may help, this occurs
only when and n dimensional system can be uniquely
represented in (n-m) dimensions.
 If the system is reconstructed with less than required
dimensions, overlap points occur as shown in the
figure.
12/9/2014 2:24:32 PM College of Engineering, Pune. 15

16.  Continued…………….
The overlap in above figure can be removed by adding
extra dimensions to the graph by means of new delay
co-ordinates.
 This process is repeated till all the overlaps are
removed.
12/9/2014 2:24:32 PM College of Engineering, Pune. 16

17. Correlation Dimension
 It gives the dimensionality of the space occupied by a
set of random points, often referred to as a type of fractal
dimension.
 It is a measure of the extent to which the presence of a data
point affects the position of the other point lying on the
attractor.
 If correlation dimensions value is finite low and non-integer,
the system is chaotic.
 If correlation exponent increases without bound with
increase in the embedding dimensions, the system is
stochastic.
12/9/2014 2:24:32 PM College of Engineering, Pune. 17

18. Largest Lyapunov Exponent Calculation &
Prediction
 After the correct reconstructed phase space plot is
configured, Lyapunov exponent for each is
calculated and the largest among them all is
selected for future prediction.
 The period limit on accurate prediction of a chaotic
system is a function of largest Lyapunov Exponent.
 To be chaotic, the largest Lyapunov exponent must
be between zero and one.
 If Lyapunov exponent is greater than one, the system
is stochastic.
12/9/2014 2:24:32 PM College of Engineering, Pune. 18

19. Algorithm :
1. Start with unfolded attractor in m-dimensional space
and time lag τ.
2. Take the initial vector y(t1).
3. Select the k nearest trajectories on the attractor.
4. Afterwards select the respective k nearest points to
y(t1), one on each trajectory.
5. An average of all these trajectories is calculated
6. The determined value is used to point next point on
predicted trajectory.
7. The predicted point is then set as a new starting
vector and the process is repeated.
12/9/2014 2:24:32 PM College of Engineering, Pune. 19

20. References
 Arslan Basharat, Mubarak Shah, “Time Series
Prediction by Chaotic Modeling of Nonlinear
Dynamical Systems,” IEEE cpnference 2009.
 Pengjian Shang, Xuewei Li, Santi Kamae, “Chaotic
analysis of traffic time series,” IEEE conference 2004.
H. D. I. Abarbanel, “Analysis of Observed Chaotic
Data,” Springer, 1995.
 Steven H. Strogatz, “Non-linear Dynamics and Chaos
with applications to Physics, Biology, Chemistry and
Engineering,” Westview Press. Perseus Publishing,
2004.
12/9/2014 2:24:32 PM College of Engineering, Pune. 20

21. Thank You…..
12/9/2014 2:24:32 PM College of Engineering, Pune. 21