The document presents a seminar on chaotic systems, discussing key concepts such as sensitive dependence on initial conditions (the butterfly effect) and the deterministic nature of chaotic behavior. It explores various examples of chaotic systems, including weather patterns and population dynamics, and introduces methodologies for quantifying chaos using Lyapunov exponents. Additionally, the seminar highlights applications of chaos theory in cryptography, random number generation, and image encryption.

1. Seminar on
Chaotic System
Presented By;
AMIRUL HAQUE
16MCS001
MUHAMMAD HAMID
16MCS012

2. Introduction
 Chaos refers to the complex, difficult-to-predict behavior found in
nonlinear systems.
 The first recorded instance of someone noticing chaotic behavior in
a simple system was Edward Lorenz in 1960, while studying
mathematical models of weather.
 One of the important properties of chaos is “sensitive dependence
on initial conditions”, informally known as “the Butterfly Effect”.
 Sensitive dependence on initial conditions means that a very small
change in the initial state of a system can have a large effect on its
later state.

3. Cont..
Motion of double compound pendulum Lorenz attractor

4. Cont..
 When we say a chaotic system is “unpredictable”, we do not mean
that it is nondeterministic.
• A deterministic system is one that always gives the same
results for the same input/initial values.
• Real-world chaotic systems are “unpredictable” in practice
because we can never determine our input values exactly.
Thus, sensitive dependence on initial conditions will always
mess up our results, eventually.
 A chaotic system does not need to be very complex

5. Characteristics of Chaotic Systems
 They are aperiodic.
 They exhibit sensitive dependence on initial conditions and
unpredictable in the long term.
 They are governed by one or more control parameters, a small change in
which can cause the chaos to appear or disappear.
 Their governing equations are nonlinear.
 Chaotic system will produce the same results if given the same inputs, it
is unpredictable in the sense that you can not predict in what way the
system's behavior will change for any change in the input to that system. a
random system will produce different results when given the same inputs.

6. Motivation
 Contained in the field on nonlinear dynamics- evolves in time
 Chaos theory offers ordered models for seemingly disorderly systems, such
as:
 Weather patterns
 Turbulent Flow
 Population dynamics
 Stock Market Behavior
 Traffic Flow
 Nonlinear circuits

7. Example of Chaotic System
 The Solar System (Poincare)
 The Weather (Lorenz)
 Turbulence In Fluids
 Population Growth
 Lots And Lots Of Other Systems…

8. Different Type Of Chaotic Maps
 One dimensional and multi-dimensional,
 Logistic map [One Dimensional]
With one parameter
𝑋 𝑁+1 = 𝑢𝑋 𝑁(1 − 𝑋 𝑁)
where
 Sine map
𝑥 𝑛+1= f (r,x,n) = r x sin(π×𝑥 𝑛)
where r Ɛ (0,4]

9. Cont..
 Tent map -Tent-like shape in the graph of its bifurcation diagram.
𝑥 𝑛+1 = T (u,𝑥 𝑛)={ u𝑥 𝑛/2 𝑥𝑖 < 0.5
u(1-𝑥 𝑛)/2 𝑥𝑖 > 0.5

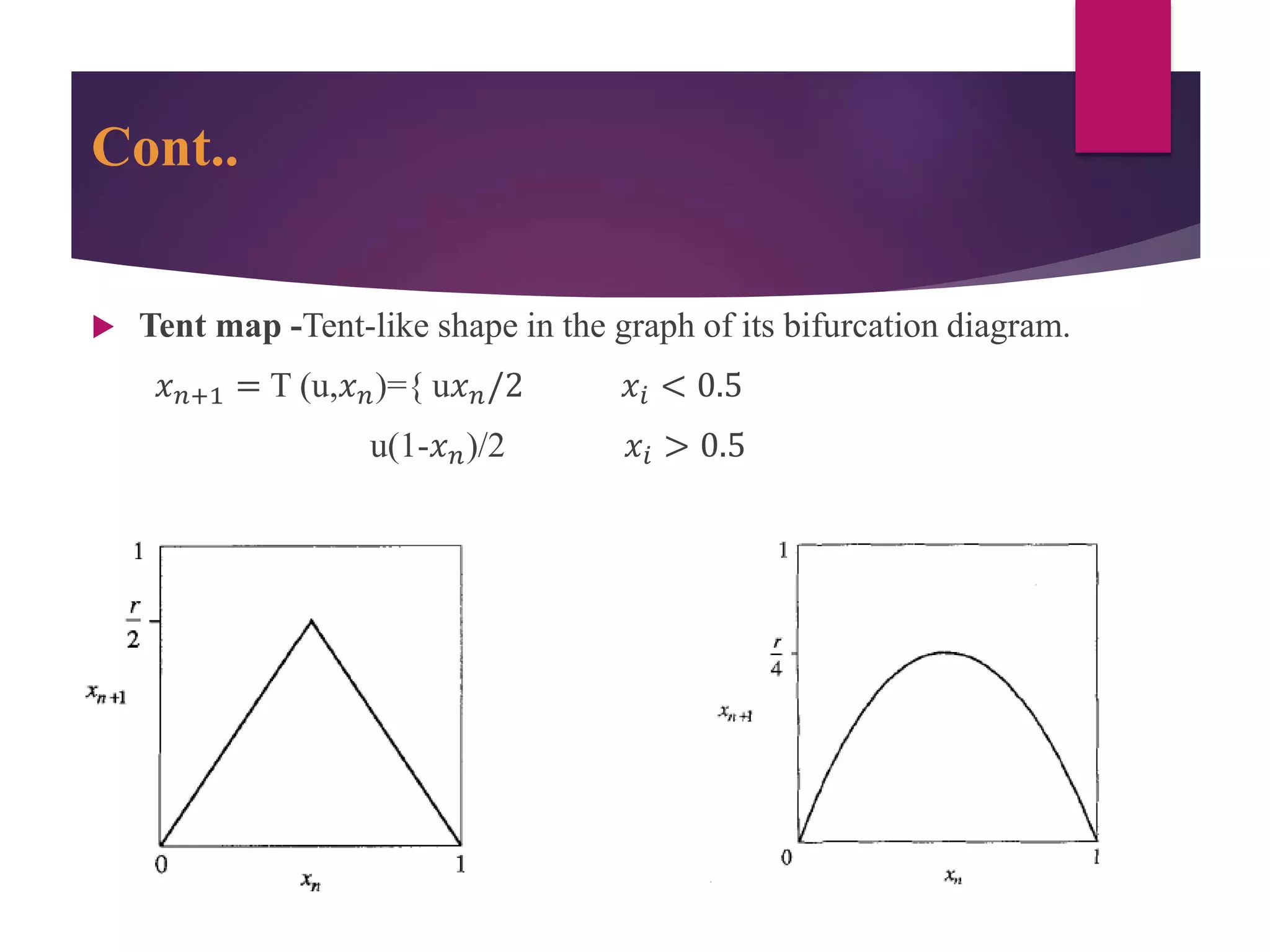
10. Cont..
.
Chaotic Henon Map [2 dimensional]
The Henon map is a 2-D iterated map with chaotic solutions proposed
by Mchel Henon (1976).
2
1
1
1
(8)n n n
n n
X aX bY
Y X


   


0 0.2 0.4 0.6 0.8 1 1.2 1.4
-1.5
-1
-0.5
0
0.5
1
1.5
Bifurcation diagram for the Henon map,
b=0.3

11. -30
-20
-10
0
10
20
-40
-20
0
20
40
0
10
20
30
40
50
z
xy
0 20 40 60 80 100 120 140 160 180 200
-20
0
20
time
x
0 20 40 60 80 100 120 140 160 180 200
-50
0
50
time
y
0 20 40 60 80 100 120 140 160 180 200
0
50
100
time
z
system parameters： a=10; b=28; c=8/3
Initial values： x0=-7.69; y0=-15.61; z0=90.39
( )x a y x
y bx y xz
z xy cz
 

  
  
&
&
&
• The Lorenz system – by Edward Lorenz(1963)
Cont..

12. Bifurcation
 The logistic map shows a variety of behaviors and it has transitions
between these behaviors as we change the parameter r. Such transitions in
dynamical systems are called bifurcations.
 Bifurcation is a scientific way to say something splits in two—branches.
 If patterns bifurcate quickly enough, they can become complex very fast,
leading to bifurcation cascade and chaos.

13. Cont..
 Bifurcation diagrams

14. Lyapunov Exponents
 Gives a measure for the predictability of a dynamic system
• characterizes the rate of separation of infinitesimally close trajectories
• Describes the average rate which predictability is lost
 Usually Calculate the Maximal Lyapunov Exponent
• Gives the best indication of predictability
• Positive value usually taken as an indication that the system is chaotic
• d(t) is the separation of the trajectories

15. How to quantify chaos?
0
)(
ln
1
lim
d
td
tt 

The Lyapunov exponent characterizes the rate of exponential divergence of nearby
orbits
It is formally defined as:
Therefore, if d(t) = d0 exp n(t-t0), then λ = n, and λ = 0 otherwise
The rate of divergence may depend on the orientation of the d0 vector
d0 d(t)

16. Cont..
 Lyapunov Exponents - defined as the average rates of exponential
divergence or convergence of nearby trajectories.
 The quantity whose sign indicates chaos and its value measures the
rate at which initial nearby trajectories exponentially diverge.
 A positive maximal Lyapunov exponent is a signature of chaos.

17. Cont..
 Lyapunov exponents are defined as the long time average exponential
rates of divergence of nearby states.
 If a system has at least one positive Lyapunov exponent, than the system
is chaotic.
 The larger the positive exponent, the more chaotic the system become.

18. Cont..
 Lyapunov exponents

19. Chaotic System in Cryptography
 Chaotic maps are used in generating the security key.
 Various chaotic map schemes with improved properties have been
proposed this can be classified as
a) Generating new chaotic sequences by modifying the exiting chaotic
map
b) Generating new chaotic sequences by using the sum of output chaotic
sequence of two chaotic map.
c) Generating new chaotic sequences by converting two 1D chaotic maps
into 2D chaotic map.
d) Generating new chaotic sequences by using the output sequence of one
chaotic map as initial values of other chaotic map

20. Examples
1) 𝑋 𝑁+1 = 𝐹 𝑢, 𝑥 𝑛, 𝑘
= 𝑓𝑐ℎ𝑎𝑜𝑠 𝑢, 𝑥 𝑛 ∗ 𝐺 𝐾 − 𝑓𝑙𝑜𝑜𝑟(𝑓𝑐ℎ𝑎𝑜𝑠 𝑢, 𝑥 𝑛 ∗ G 𝐾
2) 𝑋 𝑁+1 = 𝐹 𝑎, 𝑥 𝑛 = (𝑓 𝑎, 𝑥 𝑛 + 𝐺 𝑏, 𝑥 𝑛 )mod1
 Check the chaotic behavior in deferent combination of chaotic maps like
logistic map, sine map etc.
 Perform verification of New Chaotic System various diagrams
 Bifurcation diagrams
 Lyapunov exponents
 Information Entropy

21. APPLICATIONS
 Random Number generator
 Chaotic Communication
 Chaos in image encryption
 Chaotic Neuronal Networks
 Genetic networks
 Design of Chaotic Circuit

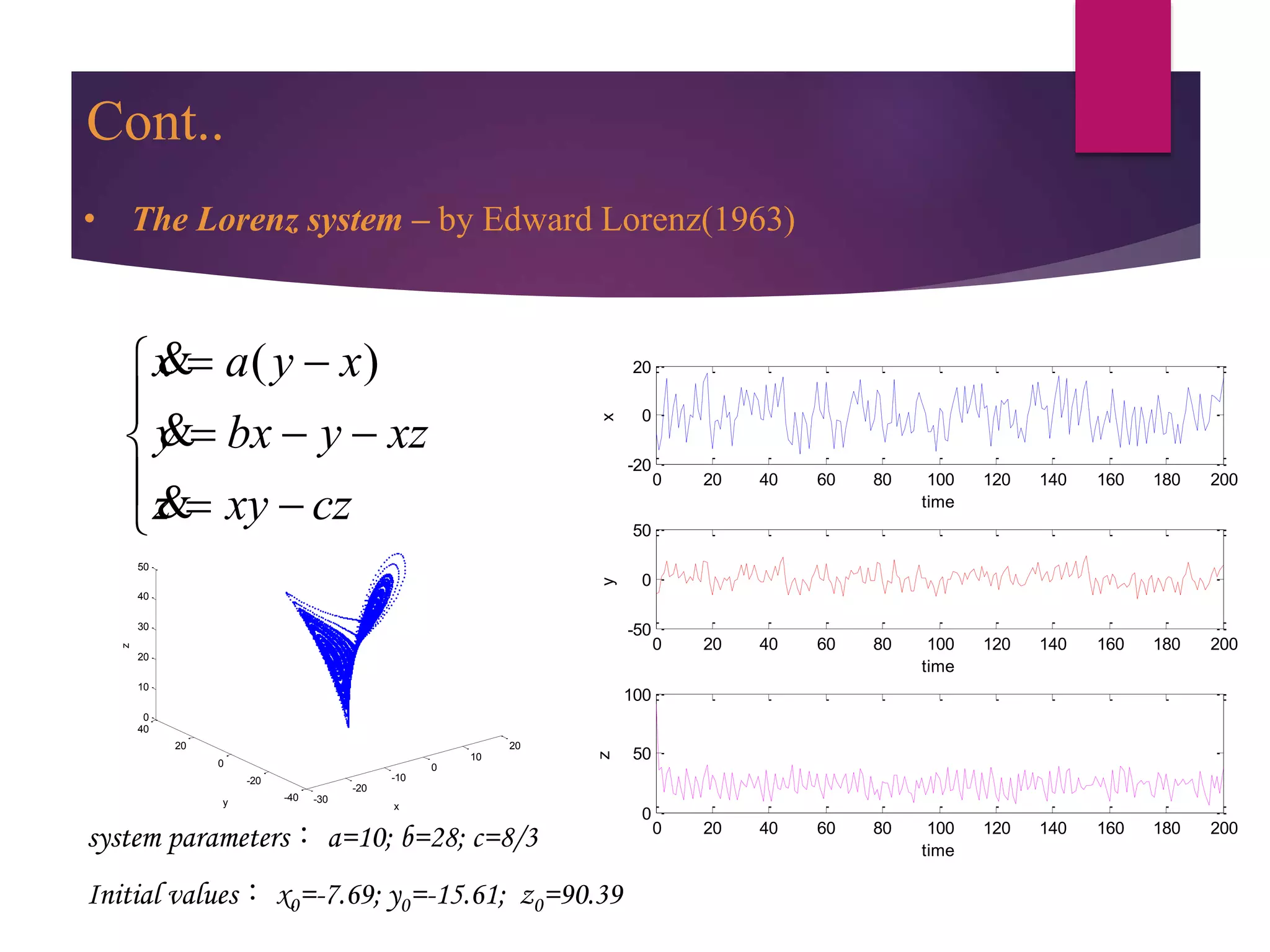
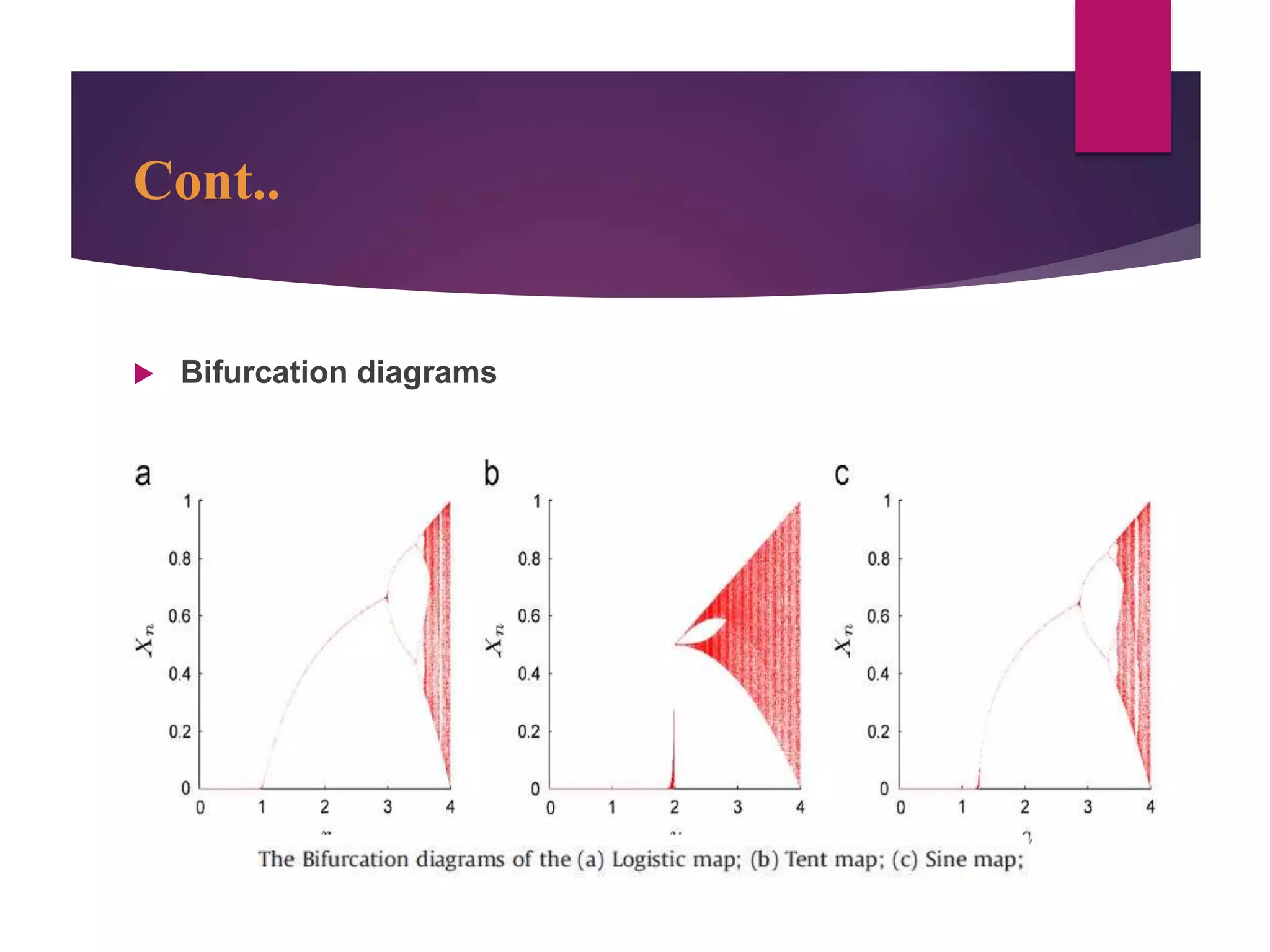
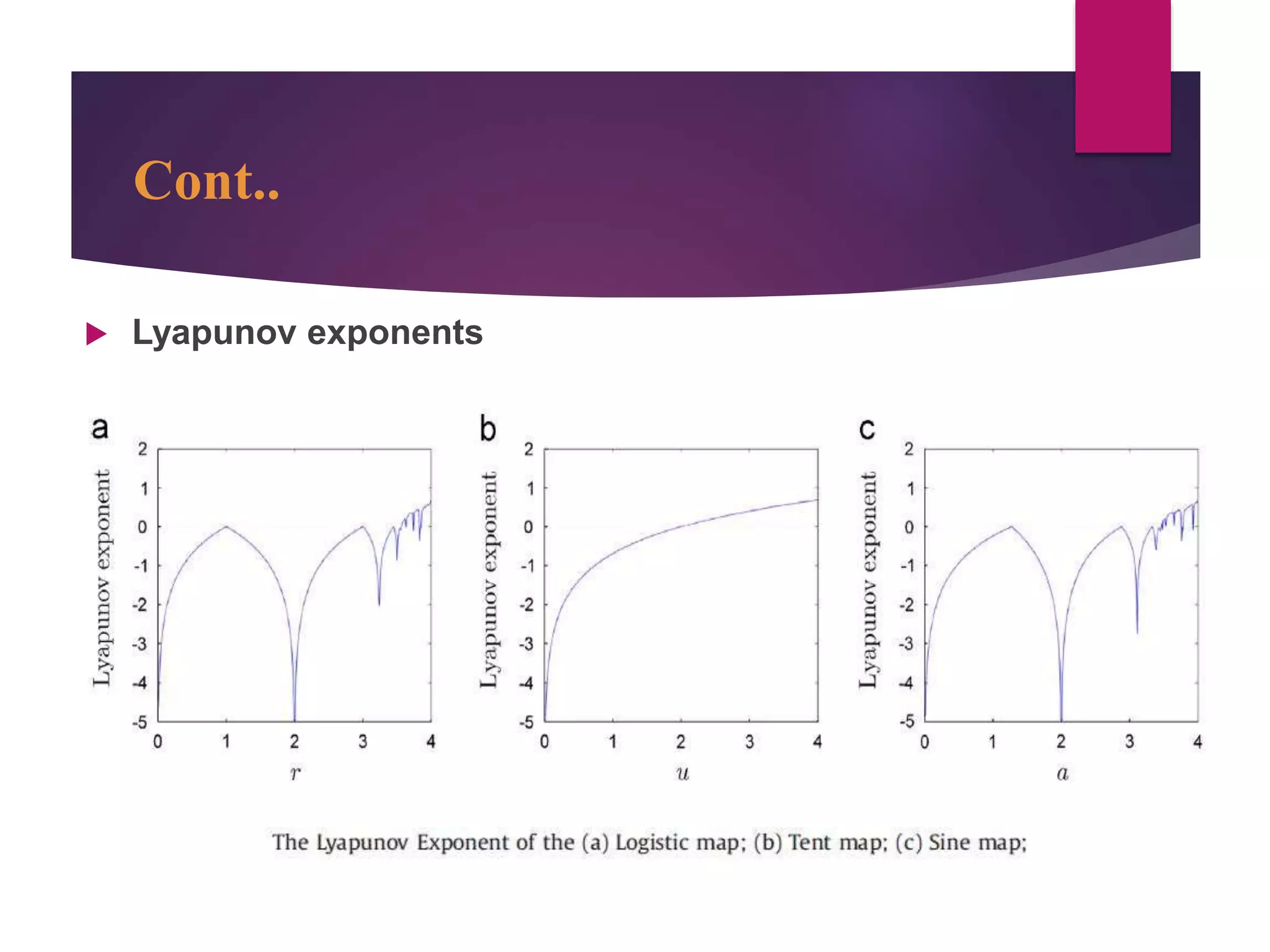
22. References
 [1] Chanil Pak, Lilian Huang, A new color image encryption using
combination of 1D chaotic map, Signal Process.138 (2017) 129–137.
 [2] Nigel Crook and Tjeerd olde Scheper, A Novel Chaotic Neural
Network Architecture
 [3] Chaos and Time-Series Analysis, by J.C. Sprott, Oxford Press 2006
 [4] S. M. Chang, M. C. Li and W. W. Lin, Asymptotic synchronization of
modified logistic hyper-chaotic systems and its applications. Nonlinear
Analysis: Real World Applications, Vol. 10, Issue 2 (2009), pp. 869–880.
 [5] Nigel Crook and Tjeerd olde Scheper, A Novel Chaotic Neural
Network Architecture

23. THANK YOU !!!