The document presents John Alexander Vargas' research proposal for exploring the use of the utcc calculus with spatial logic as the underlying logic for modeling mobile properties of concurrent systems. The methodology involves defining a spatial constraint system, modeling a simple example using utcc and spatial constraints, verifying spatial properties, and modeling a complex multi-cellular system. Spatial logic is introduced for specifying properties of mobile systems, with logical inference rules and a sequent calculus for deciding validity presented.

1. Introduction
Concurrent Constraint System
A Simple Example
A Spatial Concurrent-Constraint Calculus
(First Report)
John Alexander Vargas
Forces, 2009
John Alexander Vargas A Spatial Concurrent-Constraint Calculus (First Report)

2. Introduction
Concurrent Constraint System
A Simple Example
Preliminars
The Concurrent Constraint Programing is a formalism for
reasoning about agents which interact with each other by
telling and asking information represented as logic formulas
The agent can viewed as both process and formulas in the
underlying logic.
The Ambient Calculus model de behavior and structure of
mobile systems.
The Spatial Logic can be use to specify properties of these
systems.
The utcc calculus allow for the specication of mobile
behaviors in the sense of π-calculus
John Alexander Vargas A Spatial Concurrent-Constraint Calculus (First Report)

3. Introduction
Concurrent Constraint System
A Simple Example
Research Proposal
The BioAmbients Calculus is an abstraction for biomolecular
systems using the π-calculus for modeling molecular and
biochemical aspects and ambients calculus for specication of
process location and movement.
Mi research proposal is explore the use utcc with spatial logic
as underlyng logic of constraint system for modeling mobile
properties.
Model and study a complex multi-cellular system: The
hypothalamic weight regulation system
John Alexander Vargas A Spatial Concurrent-Constraint Calculus (First Report)

4. Introduction
Concurrent Constraint System
A Simple Example
Metodology
The metodology is:
1 To dene formaly a constraint system with spatial logic as
underlyng logic.
2 To model a simple example with utcc and spatial constraint
system.
3 Verify spatial properties that satisfy with this calculus.
4 To model the hypothalamic weight regulation system with this
calculus.
5 Verify that mobile properties can be modeled with this
calculus.
John Alexander Vargas A Spatial Concurrent-Constraint Calculus (First Report)

5. Introduction
Concurrent Constraint System
A Simple Example
Outline
1 Introduction
2 Concurrent Constraint System
Spatial Logic
Logical Inference Rules
Deciding Validity by Deduction
3 A Simple Example
Modeling Ambients in utcc
Firewall and Agent
Rules of Satisfaction of utcc process
John Alexander Vargas A Spatial Concurrent-Constraint Calculus (First Report)

6. Introduction
Concurrent Constraint System
A Simple Example
Spatial Logic
Logical Inference Rules
Deciding Validity by Deduction
Outline
1 Introduction
2 Concurrent Constraint System
Spatial Logic
Logical Inference Rules
Deciding Validity by Deduction
3 A Simple Example
Modeling Ambients in utcc
Firewall and Agent
Rules of Satisfaction of utcc process
John Alexander Vargas A Spatial Concurrent-Constraint Calculus (First Report)

7. Introduction
Concurrent Constraint System
A Simple Example
Spatial Logic
Logical Inference Rules
Deciding Validity by Deduction
Logical Formulas and Satisfaction
John Alexander Vargas A Spatial Concurrent-Constraint Calculus (First Report)

8. Introduction
Concurrent Constraint System
A Simple Example
Spatial Logic
Logical Inference Rules
Deciding Validity by Deduction
Example
P a[m[out a.inb. c ]]|b[openm.(n).n[]]
P |= a[T]|b[T]|T P includes locations a and b
P |= a[m[T]]|T there is a location m in a
P |= ♦(b[m[T]|T]) a location m will be found in b
P |= ♦ c[] an empty location c will be produced
(a[m[T]]|T)∧ ♦(b[m[T]|T])
John Alexander Vargas A Spatial Concurrent-Constraint Calculus (First Report)

9. Introduction
Concurrent Constraint System
A Simple Example
Spatial Logic
Logical Inference Rules
Deciding Validity by Deduction
Quantiers
Fresh-Name Quantier
P |= x.A ∃m ∈ Λ, m /∈ fn(P,A)∧P |= A{x ← m}
P |= x.A ∀m ∈ Λ, m /∈ fn(P,A)∧P |= A{x ← m}
because any fresh name is as good as any other.
Hidden-Name Quantier
P |=Hx.Ai ∃m ∈ Λ, P /∈ Πm /∈ fn(A)∧P ≡ (v m)P ∧P |=
A{x ← m}
Hx.A x.x R A
John Alexander Vargas A Spatial Concurrent-Constraint Calculus (First Report)

10. Introduction
Concurrent Constraint System
A Simple Example
Spatial Logic
Logical Inference Rules
Deciding Validity by Deduction
Describing spatial properties of concurrent systems
This Spatial Logics are used to specify the behavior and spatial
structure of concurrent systems, properties as a fresh or secret
resources such as keys, nonces, channels, and locations.
John Alexander Vargas A Spatial Concurrent-Constraint Calculus (First Report)

11. Introduction
Concurrent Constraint System
A Simple Example
Spatial Logic
Logical Inference Rules
Deciding Validity by Deduction
Outline
1 Introduction
2 Concurrent Constraint System
Spatial Logic
Logical Inference Rules
Deciding Validity by Deduction
3 A Simple Example
Modeling Ambients in utcc
Firewall and Agent
Rules of Satisfaction of utcc process
John Alexander Vargas A Spatial Concurrent-Constraint Calculus (First Report)

12. Introduction
Concurrent Constraint System
A Simple Example
Spatial Logic
Logical Inference Rules
Deciding Validity by Deduction
Propositional
John Alexander Vargas A Spatial Concurrent-Constraint Calculus (First Report)

13. Introduction
Concurrent Constraint System
A Simple Example
Spatial Logic
Logical Inference Rules
Deciding Validity by Deduction
Composition
John Alexander Vargas A Spatial Concurrent-Constraint Calculus (First Report)

14. Introduction
Concurrent Constraint System
A Simple Example
Spatial Logic
Logical Inference Rules
Deciding Validity by Deduction
Locations
John Alexander Vargas A Spatial Concurrent-Constraint Calculus (First Report)

15. Introduction
Concurrent Constraint System
A Simple Example
Spatial Logic
Logical Inference Rules
Deciding Validity by Deduction
Modalities
John Alexander Vargas A Spatial Concurrent-Constraint Calculus (First Report)

16. Introduction
Concurrent Constraint System
A Simple Example
Spatial Logic
Logical Inference Rules
Deciding Validity by Deduction
Revelation
John Alexander Vargas A Spatial Concurrent-Constraint Calculus (First Report)

17. Introduction
Concurrent Constraint System
A Simple Example
Spatial Logic
Logical Inference Rules
Deciding Validity by Deduction
Example of Deduction
John Alexander Vargas A Spatial Concurrent-Constraint Calculus (First Report)

18. Introduction
Concurrent Constraint System
A Simple Example
Spatial Logic
Logical Inference Rules
Deciding Validity by Deduction
Outline
1 Introduction
2 Concurrent Constraint System
Spatial Logic
Logical Inference Rules
Deciding Validity by Deduction
3 A Simple Example
Modeling Ambients in utcc
Firewall and Agent
Rules of Satisfaction of utcc process
John Alexander Vargas A Spatial Concurrent-Constraint Calculus (First Report)

19. Introduction
Concurrent Constraint System
A Simple Example
Spatial Logic
Logical Inference Rules
Deciding Validity by Deduction
Spatial Logic for nite trees
Due to the growing popularity of semistructured data, and
particularly XML, there is a renewed interest in typed
programming languages that can manipulate tree-like data
structures.
Spatial Logics was proposed as a rich description language for
tree-like data.
View the spatial logics as a type system to semi-structured
data.
John Alexander Vargas A Spatial Concurrent-Constraint Calculus (First Report)

20. Introduction
Concurrent Constraint System
A Simple Example
Spatial Logic
Logical Inference Rules
Deciding Validity by Deduction
Sequent Calculus
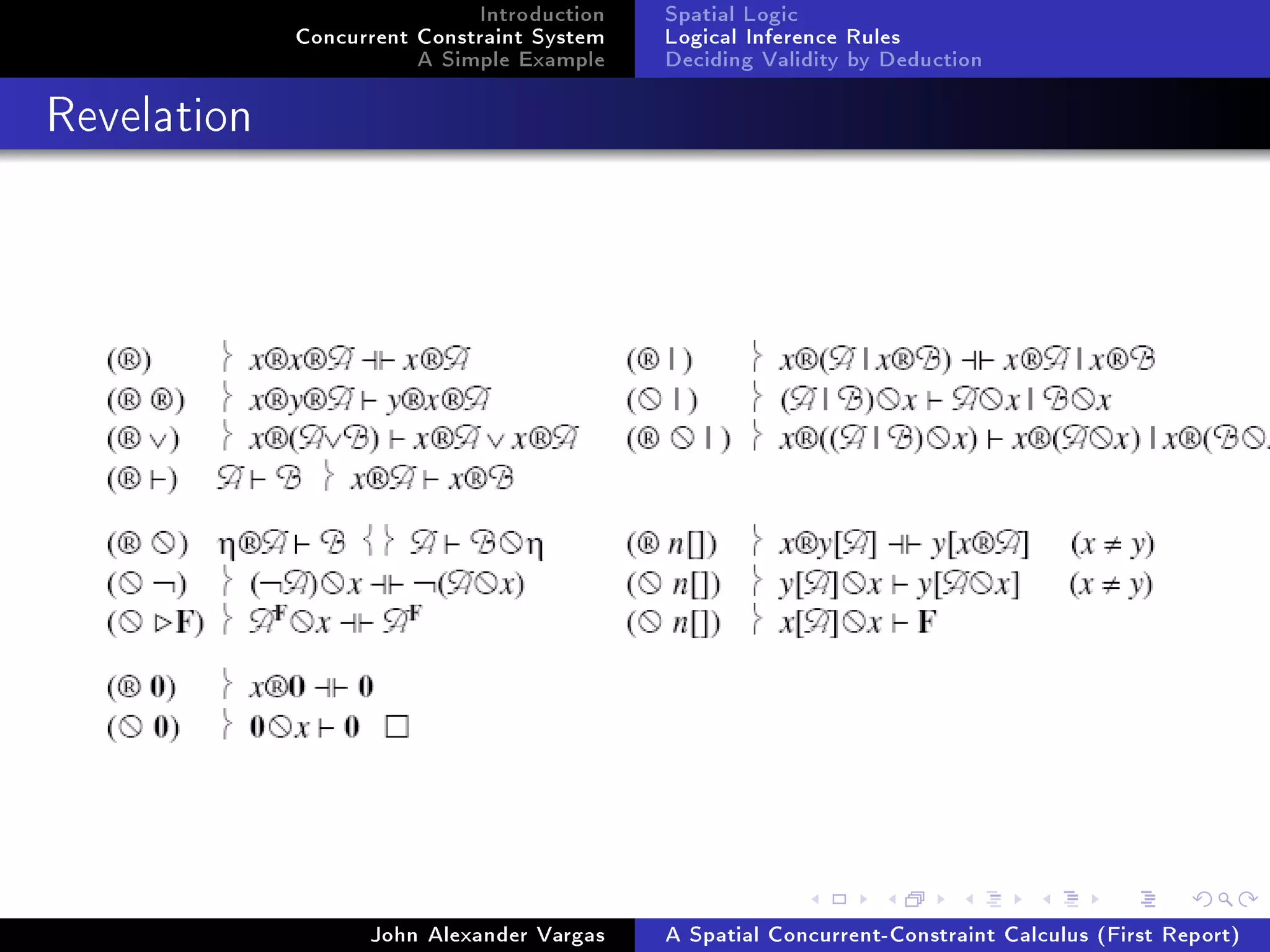
In [CalCarGor02] presented a sequent calculus for spatial logics
of ambients. And show that this calculus is sound and
complete with respect to an interpretation in terms of the
satisfaction relation, and present a complete proof procedure.
A context, Γ or ∆, is a nite multiset of entries of the form
P : A where P is a tree and A is a formula. A sequent is a
judgment Γ ∆ ` where Γ and ∆ are contexts.
John Alexander Vargas A Spatial Concurrent-Constraint Calculus (First Report)

21. Introduction
Concurrent Constraint System
A Simple Example
Spatial Logic
Logical Inference Rules
Deciding Validity by Deduction
Rules of the sequents calculus
John Alexander Vargas A Spatial Concurrent-Constraint Calculus (First Report)

22. Introduction
Concurrent Constraint System
A Simple Example
Spatial Logic
Logical Inference Rules
Deciding Validity by Deduction
Rules of Sequent Calculus
John Alexander Vargas A Spatial Concurrent-Constraint Calculus (First Report)

23. Introduction
Concurrent Constraint System
A Simple Example
Spatial Logic
Logical Inference Rules
Deciding Validity by Deduction
Decidability
Theorem
(Complete Proof Procedure)
For any Γ ∆ there is a procedure such that: if ¬[[Γ ∆]], then
the procedure terminates with failure; if [[Γ ∆]], then the
procedure terminates with a derivation for Γ ∆ .
John Alexander Vargas A Spatial Concurrent-Constraint Calculus (First Report)

24. Introduction
Concurrent Constraint System
A Simple Example
Modeling Ambients in utcc
Firewall and Agent
Rules of Satisfaction of utcc process
Outline
1 Introduction
2 Concurrent Constraint System
Spatial Logic
Logical Inference Rules
Deciding Validity by Deduction
3 A Simple Example
Modeling Ambients in utcc
Firewall and Agent
Rules of Satisfaction of utcc process
John Alexander Vargas A Spatial Concurrent-Constraint Calculus (First Report)

25. Introduction
Concurrent Constraint System
A Simple Example
Modeling Ambients in utcc
Firewall and Agent
Rules of Satisfaction of utcc process
Modeling Ambients in utcc with Spatial Logics
P a[inb.P], Q b[0], then the reduction of P|Q
a[inb.R]|b[0] → b[a[R]]
P tell (a[R]) || (abs T1,T2; a[T1]|b[T2]) tell (b[a[T1]|T2])
Q tell (b[0])
P a[outb.R], then the reduction of b[P]
b[a[outb.R]] → b[0]|a[R]
P tell (a[R]) || (abs T1,T2; b[a[T1]|T2]) tell ( b[T2]|a[T1] )
Q tell (b[a[R]])
P openb.R, Q b[S], then the reduction of P|Q
openb.R|b[S] → R|S
P tell ( R ) (abs T1, T2; b[T1]|T2) tell (T1 |T2)
Q tell (b[R])
John Alexander Vargas A Spatial Concurrent-Constraint Calculus (First Report)

26. Introduction
Concurrent Constraint System
A Simple Example
Modeling Ambients in utcc
Firewall and Agent
Rules of Satisfaction of utcc process
Modeling Ambients in utcc with Spatial Logics
P a[inb.P], Q b[0], then the reduction of P|Q
a[inb.R]|b[0] → b[a[R]]
P tell (a[R]) || (abs T1,T2; a[T1]|b[T2]) tell (b[a[T1]|T2])
Q tell (b[0])
P a[outb.R], then the reduction of b[P]
b[a[outb.R]] → b[0]|a[R]
P tell (a[R]) || (abs T1,T2; b[a[T1]|T2]) tell ( b[T2]|a[T1] )
Q tell (b[a[R]])
P openb.R, Q b[S], then the reduction of P|Q
openb.R|b[S] → R|S
P tell ( R ) (abs T1, T2; b[T1]|T2) tell (T1 |T2)
Q tell (b[R])
John Alexander Vargas A Spatial Concurrent-Constraint Calculus (First Report)

27. Introduction
Concurrent Constraint System
A Simple Example
Modeling Ambients in utcc
Firewall and Agent
Rules of Satisfaction of utcc process
Modeling Ambients in utcc with Spatial Logics
P a[inb.P], Q b[0], then the reduction of P|Q
a[inb.R]|b[0] → b[a[R]]
P tell (a[R]) || (abs T1,T2; a[T1]|b[T2]) tell (b[a[T1]|T2])
Q tell (b[0])
P a[outb.R], then the reduction of b[P]
b[a[outb.R]] → b[0]|a[R]
P tell (a[R]) || (abs T1,T2; b[a[T1]|T2]) tell ( b[T2]|a[T1] )
Q tell (b[a[R]])
P openb.R, Q b[S], then the reduction of P|Q
openb.R|b[S] → R|S
P tell ( R ) (abs T1, T2; b[T1]|T2) tell (T1 |T2)
Q tell (b[R])
John Alexander Vargas A Spatial Concurrent-Constraint Calculus (First Report)

28. Introduction
Concurrent Constraint System
A Simple Example
Modeling Ambients in utcc
Firewall and Agent
Rules of Satisfaction of utcc process
Spatial Formulas in utcc
P tell (n[R] m[S])
Q (abs T1; m[T1]) tell R@n
P||Q|| tell n[R]
John Alexander Vargas A Spatial Concurrent-Constraint Calculus (First Report)

29. Introduction
Concurrent Constraint System
A Simple Example
Modeling Ambients in utcc
Firewall and Agent
Rules of Satisfaction of utcc process
Outline
1 Introduction
2 Concurrent Constraint System
Spatial Logic
Logical Inference Rules
Deciding Validity by Deduction
3 A Simple Example
Modeling Ambients in utcc
Firewall and Agent
Rules of Satisfaction of utcc process
John Alexander Vargas A Spatial Concurrent-Constraint Calculus (First Report)

30. Introduction
Concurrent Constraint System
A Simple Example
Modeling Ambients in utcc
Firewall and Agent
Rules of Satisfaction of utcc process
Example in Ambient Calculus
Firewall (vw)w[k[out w.ink .inw]|openk .openk .P]
Agent k [openk.k [Q]]
(v k k k )(Agent |Firewall) ∼= (v w)w[Q |P]
John Alexander Vargas A Spatial Concurrent-Constraint Calculus (First Report)

31. Introduction
Concurrent Constraint System
A Simple Example
Modeling Ambients in utcc
Firewall and Agent
Rules of Satisfaction of utcc process
Example in tcc
Firewall Agent
(local w) tell ( k [k [Q]] ) ||
tell (w[P]|k[0]) || (abs T1,T2 ; k [k[T1]|T2])
(abs T1,T2 ; k [T1]|k[T2] ) (tell ( k [T1|T2] ) )
( tell ( k [k[T2]|T1] ) ||
(abs A,B ; w[A]|k [B] )
(tell ( w[A|k [B]] ))
) ||
(abs T1,T2 ; w[k [T1]|T2])
( tell (w[T1|T2]) ||
(abs A,B ; w[k [A]|B] )
( tell (w[A|B]) )
)
John Alexander Vargas A Spatial Concurrent-Constraint Calculus (First Report)

32. Introduction
Concurrent Constraint System
A Simple Example
Modeling Ambients in utcc
Firewall and Agent
Rules of Satisfaction of utcc process
Outline
1 Introduction
2 Concurrent Constraint System
Spatial Logic
Logical Inference Rules
Deciding Validity by Deduction
3 A Simple Example
Modeling Ambients in utcc
Firewall and Agent
Rules of Satisfaction of utcc process
John Alexander Vargas A Spatial Concurrent-Constraint Calculus (First Report)

33. Introduction
Concurrent Constraint System
A Simple Example
Modeling Ambients in utcc
Firewall and Agent
Rules of Satisfaction of utcc process
Satisfaction
tell (c) |= c
P|=A
(localx,c)P|=Hx.A
P|=A
(absx,c)P|=Nx.c∧Hx.A
P|=A∧Q|=B
P|Q|=A|B
P|=A
nextP|=◦A
John Alexander Vargas A Spatial Concurrent-Constraint Calculus (First Report)

34. Introduction
Concurrent Constraint System
A Simple Example
Modeling Ambients in utcc
Firewall and Agent
Rules of Satisfaction of utcc process
Future Work
Study the model of hypothalamic weight regulation system in
bioambients.
Model this biological system with sccp
Study mobile properties in sccp.
John Alexander Vargas A Spatial Concurrent-Constraint Calculus (First Report)

35. Introduction
Concurrent Constraint System
A Simple Example
Modeling Ambients in utcc
Firewall and Agent
Rules of Satisfaction of utcc process
References
Cristiano Calcagno Luca Cardelli Andrew D. Gordon Deciding
Validity in a Spatial Logic for Trees, 2002
Luca Cardelli, Adrew Gordon. Logical Properties of Name
Restriction.
Luca Cardelli y Andrew Gordón. Mobile Ambients. 1997.
Luca Cardelli y Andrew Gordon. Ambient Logic. 2003
Luis Caires y Luca Cardelli. A Spatial Logic for Concurrency
(Part I). 2007
Carlos Olarte, Catuscia Palamidesi y Frank Valencia. Universal
Timed Concurrent Constraint Programming. 2007
Aviv Regev, E. Panina, W Silverman, L Cardelli y E. Shapiro.
BioAmbients: An abstraction for biological compartments. 2003
Vijay A Saraswat, Martin Rinard y Prakash Pamangaden.John Alexander Vargas A Spatial Concurrent-Constraint Calculus (First Report)