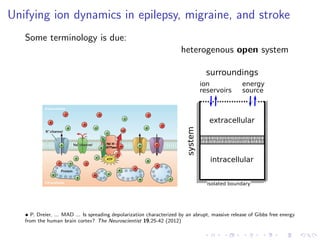
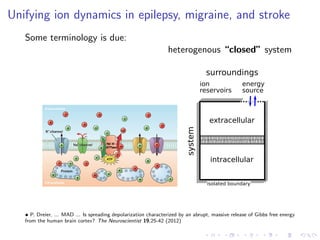
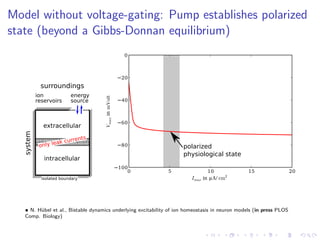
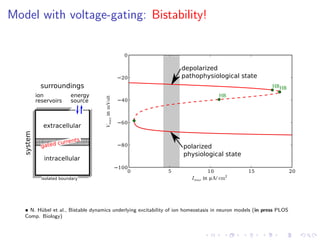
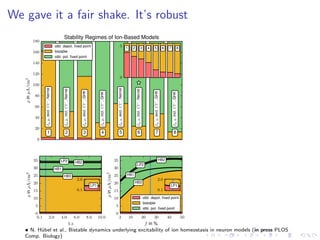
The document presents a unifying framework for modeling ion dynamics in the brain that can explain phenomena seen in epilepsy, migraine, and stroke. It introduces a second generation of Hodgkin-Huxley type models that account for ion concentrations and pumping/buffering dynamics in addition to membrane voltage dynamics. These models exhibit bistability between polarized and depolarized states, depending on parameters. The framework aims to provide a common mechanistic explanation for different neurological disorders based on shifts between stable states induced by genetic or external factors.

1. From epilepsy to migraine to stroke:
A unifying framework
(Or: Act neurons like steam engines?)
Markus A. Dahlem (HU Berlin) &
Niklas H¨ubel (TU Berlin)
Joint Focus Session DY/BP: Dynamical Patterns in Neural Systems: From
Brain Function to Dysfunction, April 1, 2014

2. Outline
Introduction
Unifying ion dynamics in the brain
Application: From genotype to phenotype
Summary

3. Outline
Introduction
Unifying ion dynamics in the brain
Application: From genotype to phenotype
Summary

4. Top three with respect to costs & burden
In Europe
27 Migraines
22 Strokes
15.5 Epilepsy
billion Euro each year.
Balak and Elmaci (2005) European
Journal of Neurology 12
“What is particularly interesting to
note is that the most recent reports
state that migraine alone is responsible
of almost 3% of disability attributable
to a specific disease worldwide, also in
consideration of its comorbidity. This
places migraine as the 8th
most
burdensome diseases, the 7th
among
non-communicable diseases and the 1st
among the neurological disorders
ranked in the GBD report.”

5. Models fill in the ‘gaps’ in clinical obervability
insidecell
outsidecell
a e
sensory aura (15min)
visual aura (0min)
behavior,
perception
sensory
processing
(a) genetics defects, e.g. FHM, CADASIL, multifactorial (GWAS)
(e) Pain, loss of function, seizing/convulsions, mental dysfunctions, impared
sensory and cognitive processing
• MAD, Migraine generator network and spreading depression dynamics as neuromodulation targets in episodic
migraine. Chaos, 23, 046101 (2013)
• MAD, Migraines and Cortical Spreading Depression, Encyclopedia of Computational Neuroscience, (in press)
CADASIL: Cerebral Autosomal-Dominant Arteriopathy with Subcortical Infarcts and Leukoencephalopathy;
FHM: Familial hemiplegic migraine; GWAS: genome-wide association study

6. Models fill in the ‘gaps’ in clinical obervability
I
II
III
IV
V
VI
0 5 10 15 20 25 30 35
time (s)
100
50
0
50
voltage(mV)
V
EK
ENa
Iapp
seizure-like
afterdischarges
depolarization block
dominance
pump current
m-gate
deactivation
begin
I -driven
repolarization
Na
+
transmembrane&
cellularlevel
molecularlevel&
genetics
b c
insidecell
outsidecell
a
off on
HY,TH
SPG
SSN
TCC
PAG
LC
RVM
TG
cortex
cranial circulation & innervation
bone
d
SD
cortico-
thalamic
action
release noxious agents
e
sensory aura (15min)
visual aura (0min)
behavior,
perception
sensory
processing
balanced excitation and
inhibition in ion-based models
organlevel
(a) genetics defects, e.g. FHM, CADASIL, multifactorial (GWAS)
(b) Hodgkin-Huxley type, single cell electrophysiology models.
(c) Neural mass/fields population models, with subpopulations having
specific synaptic receptor distribution.
(d) Local circuits, including the migraine generator network in the brainstem
(e) Pain, loss of function, seizing/convulsions, mental dysfunctions, impared
sensory and cognitive processing
• MAD, Migraine generator network and spreading depression dynamics as neuromodulation targets in episodic
migraine. Chaos, 23, 046101 (2013)
• MAD, Migraines and Cortical Spreading Depression, Encyclopedia of Computational Neuroscience, (in press)
CADASIL: Cerebral Autosomal-Dominant Arteriopathy with Subcortical Infarcts and Leukoencephalopathy;
FHM: Familial hemiplegic migraine; GWAS: genome-wide association study

7. Outline
Introduction
Unifying ion dynamics in the brain
Application: From genotype to phenotype
Summary

8. HH-type conductance-based
C
∂V
∂t
= −INa − IK − Ileak +Iapp (1)
INa = ¯gNam3
h(V − ENa)
IK = ¯gK n4
(V − EK )
Ileak = gleak(V − Vrest)
∂n
∂t
= αn(1 − n) − βn,
∂h
∂t
· · · (2) − (4)
HH: Hodgkin-Huxley

9. From HH-type conductance-based to
conductance- & ion-based models (2nd
generation model)
3Na+
2K+
K+
Na+
K+
K+
Na+
Extracellular Space
Bath/Vasculature
Neuron
Cl
Diffusion
Cl
-
-
C
∂V
∂t
= −INa − IK − Ileak−Ipump+Iapp (1)
INa = ¯gNam3
h(V − ENa)
IK = ¯gK n4
(V − EK )
Ileak = gleak(V − Vrest)
∂n
∂t
= αn(1 − n) − βn,
∂h
∂t
· · · (2) − (4)
∂[ion]e
∂t
= −
A
FVolo
Iion
∂[ion]i
∂t
=
A
FVoli
Iion (5) − · · ·
HH: Hodgkin-Huxley

10. From HH-type conductance-based to
conductance- & ion-based models (2nd
generation model)
ion
reservoirs
isolated boundary
system
surroundings
energy
source
extracellular
intracellular
C
∂V
∂t
= −INa − IK − Ileak−Ipump+Iapp (1)
INa = ¯gNam3
h(V − ENa)
IK = ¯gK n4
(V − EK )
Ileak = gleak(V − Vrest)
∂n
∂t
= αn(1 − n) − βn,
∂h
∂t
· · · (2) − (4)
∂[ion]e
∂t
= −
A
FVolo
Iion
∂[ion]i
∂t
=
A
FVoli
Iion (5) − · · ·
HH: Hodgkin-Huxley

11. Unifying ion dynamics in epilepsy, migraine, and stroke
Some terminology is due:
heterogenous open system
ion
reservoirs
isolated boundary
system
surroundings
energy
source
extracellular
intracellular
• P. Dreier, ... MAD ... Is spreading depolarization characterized by an abrupt, massive release of Gibbs free energy
from the human brain cortex? The Neuroscientist 19,25-42 (2012)

12. Unifying ion dynamics in epilepsy, migraine, and stroke
Some terminology is due:
heterogenous “closed” system
ion
reservoirs
isolated boundary
system
surroundings
energy
source
extracellular
intracellular
• P. Dreier, ... MAD ... Is spreading depolarization characterized by an abrupt, massive release of Gibbs free energy
from the human brain cortex? The Neuroscientist 19,25-42 (2012)

13. Unifying ion dynamics in epilepsy, migraine, and stroke
Some terminology is due:
heterogenous isolated “plus” system
ion
reservoirs
isolated boundary
system
surroundings
energy
source
extracellular
intracellular
• P. Dreier, ... MAD ... Is spreading depolarization characterized by an abrupt, massive release of Gibbs free energy
from the human brain cortex? The Neuroscientist 19,25-42 (2012)

14. Many, many, parameters, but most fixed by experiments
Table: Parameters for ion–based model – Part 2
Name Value & unit Description
Cm 1 µF/cm2
membrane capacitance
φ 3/msec gating time scale parameter
gl
Na 0.0175 mS/cm2
sodium leak conductance
gg
Na 100 mS/cm2
max. gated sodium conductance
gl
K 0.05 mS/cm2
potassium leak conductance
gg
K 40 mS/cm2
max. gated potassium conductance
gl
Cl 0.02 mS/cm2
chloride leak conductance
Na0
i 25.23 mM/l intracell. sodium conc.
Na0
e 125.31 mM/l extracell. sodium conc.
K0
i 129.26 mM/l intracell. potassium conc.
K0
e 4 mM/l extracell. potassium conc.
Cl0
i 9.9 mM/l intracell. chloride conc.
Cl0
e 123.27 mM/l extracell. chloride conc.
E0
Na 39.74 mV sodium Nernst potential
E0
K -92.94 mV potassium Nernst potential
E0
Cl -68 mV chloride Nernst potential

15. And still more parameters, but most fixed by experiments
Table: Parameters for ion–based model – Part 2
Name Value & unit Description
ωi 2.16 µm3
intracell. volume
ωe 0.72 µm3
extracell. volume
F 96485 C/Mol Faraday’s constant
Am 0.922 µm2
membrane surface
γ 9.556e–6 µm2
Mol
C
conversion factor
ρ 6.8 µA/cm2
max. pump current
¯k1 5e–5/sec/(mM/l) buffering rate
k1 5e–5/sec backward buffering rate
λ 3e–2/sec diffusive coupling strength
Kbath 4 mM/l potassium conc. of extracell. bath
B0
500 mM/l buffer conc.

16. Fixed points in 2nd
generation HH
“closed” system & leaky membrane
“closed” system & voltage–gated membrane
open system & voltage–gated membrane
(This will help to understand periodic solutions)

17. Model without voltage-gating: Pump establishes polarized
state (beyond a Gibbs-Donnan equilibrium)
ion
reservoirs
isolated boundary
system
surroundings
energy
source
extracellular
intracellular
only leak currents
0 5 10 15 20
Imax in µA/ cm2
100
80
60
40
20
0
VmaxinmVolt
polarized
physiological state
• N. H¨ubel et al., Bistable dynamics underlying excitability of ion homeostasis in neuron models (in press PLOS
Comp. Biology)

18. Model with voltage-gating: Bistability!
ion
reservoirs
isolated boundary
system
surroundings
energy
source
extracellular
intracellular
gated currents
0 5 10 15 20
Imax in µA/ cm2
100
80
60
40
20
0
VmaxinmVolt
HB
HBHB
polarized
physiological state
depolarized
pathophysiological state
• N. H¨ubel et al., Bistable dynamics underlying excitability of ion homeostasis in neuron models (in press PLOS
Comp. Biology)

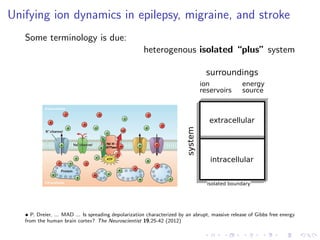
19. Choices: Current and pump equations, ions, ...
Two pump types
Iion,pumped,1([K]o, [Na]i ) = Imax 1 +
KmK
[K]o
−2
1 +
KmNa
[Na]i
−3
Iion,pumped,2([K]o, [Na]i ) = Imax
1
1 + e(25−[Na]i /3)
1
1 + e(5.5−[K]o)
HH current or GHK currents
Iion = gion(V − Eion)
Iion = V αF Pion
[ion]i − [ion]oe−αV
1 − e−αV
With or without chloride dynamics
d[Cl−]
dt
= ... or 0

20. We gave it a fair shake. It’s robust
0
20
40
60
80
100
120
140
160
180
ρinµA/cm2
Ip,B,excl.Cl−,Nernst
Ip,B,incl.Cl−,Nernst
Ip,B,excl.Cl−,GHK
Ip,B,incl.Cl−,GHK
Ip,A,excl.Cl−,Nernst
Ip,A,incl.Cl−,Nernst
Ip,A,excl.Cl−,GHK
Ip,A,incl.Cl−,GHK
1 2 3 4 5 6 7 8
Stability Regimes of Ion-Based Models
stbl. depol. fixed point
bistable
stbl. pol. fixed point
0
5 1 2 3 4 5 6 7 8
0.1 2.0 4.0 6.0 8.0 10.0
χA
0
5
10
15
20
25
30
35
ρinµA/cm2
HB1
LP2 HB2
HB3
2 10 20 30 40 50
f in %
0
5
10
15
20
25
30
35
ρinµA/cm2
HB1
LP2
HB2
HB3
stbl. depol. fixed point
bistable
stbl. pol. fixed point
0.1
2.0
LP1
0.1
2.0
LP1
• N. H¨ubel et al., Bistable dynamics underlying excitability of ion homeostasis in neuron models (in press PLOS
Comp. Biology)

21. HH 2nd
-generation “closed” systems are bistable
C
∂V
∂t
= −
ion
(Iion,gated + Iion,pumped )
current, pump, and gating equations . . .
∂[K+]e
∂t
=
A
FVole
(IK+,gated + IK+,pumped )
ion
reservoirs
isolated boundary
system
surroundings
energy
source
extracellular
intracellular
0 5 10 15 20
Imax in µA/ cm2
100
80
60
40
20
0
VmaxinmVolt
HB
HBHB
polarized
physiological state
depolarized
pathophysiological state

22. Open system: Diffusion (buffering) of potassium
C
∂V
∂t
= −
ion
(Iion,gated + Iion,pumped )
fixed point!
= 0
current, pump, and gating equations . . .
∂[K+]e
∂t
=
A
FVole
(IK+,gated + IK+,pumped )+ λ([K+
]bath − [K+
]e)
buffer to bath
fixed point!
= 0
f.p.!
= 0
ion
reservoirs
isolated boundary
system
surroundings
energy
source
extracellular
intracellular
0 5 10 15 20
Imax in µA/ cm2
100
80
60
40
20
0
VmaxinmVolt
HB
HBHB
polarized
physiological state
depolarized
pathophysiological state

23. Periodic solutions in 2nd
generation HH
open system & voltage–gated membrane
full bifurcation analysis
slow–fast analysis

24. Time scales in ion dynamics
1st generation Hodgkin–Huxley model
0.01ms RC membrane time constant
1ms ion gating
2nd generation Hodgkin–Huxley model has in addition
1s volume–to–surface–area ratio / permeability
100s potassium regulation

25. Unified minimal (4D) model of
spiking, seizures and spreading depression
5 10 15 20
Kbath / (mM/l)
−150
−100
−50
0
50
mV
HB1
LP1
LP2 HB2 HB3
HB4
LP1lc
LP2lc
TR1
TR2TR3TR4
PD
membrane potential
5 10 15 20
Kbath / (mM/l)
0
10
20
30
40
50
60
70
80
90
mM/l
HB1
LP2
LP1
HB2
HB3
HB4
extrac. potassium
stable FP
unstable FP
stable LC
unstable LC
stable torus
0 100 200 300 400 500
t / sec.
−100
−80
−60
−40
−20
0
20
40
60
mV
potential
EK
ENa
ECl
V
0.0 0.5 1.0 1.5 2.0
t / sec.
−80
−60
−40
−20
0
20
40
60
mV
0 500 1000 1500 2000
t / sec.
−100
−80
−60
−40
−20
0
20
40
60
mV
120
130
140
ion conc.
0 100 200 300 400 500
t / sec.
10
20
120
130
0.0 0.5 1.0 1.5 2.0
t / sec.
15
20
0 500 1000 1500 2000
t / sec.
0
20
40
60
80
100
120
140
mM/l
Ki
Nai
Cli
Ke
Nae
Cle
a)
b)
c)
mM/lmM/l

26. Unified minimal (4D) model of
spiking, seizures and spreading depression
5 10 15 20
Kbath / (mM/l)
−150
−100
−50
0
50
mV
HB1
LP1
LP2 HB2 HB3
HB4
LP1lc
LP2lc
TR1
TR2TR3TR4
PD
membrane potential
5 10 15 20
Kbath / (mM/l)
0
10
20
30
40
50
60
70
80
90
mM/l
HB1
LP2
LP1
HB2
HB3
HB4
extrac. potassium
stable FP
unstable FP
stable LC
unstable LC
stable torus
5 10 15 20
Kbath / (mM/l)
20
40
60
80
100
120
140
160
mM/l
LP1
LP2
HB1
HB2
HB3
HB4
LP1lc
LP2lc
TR1
TR2
TR3
TR4
extrac. sodium
5 10 15 20
Kbath / (mM/l)
−80
−60
−40
−20
0
20
40
mM/l
LP1
LP2
HB1
HB2 HB3
HB4
LP1lc
LP2lc
TR1
TR2
TR3
TR4
potassium gain/loss ˜Ke
stable FP
unstable FP
stable LC
unstable LC
stable torus
6.7 6.9 7.1
HB1 TR4
PD

27. Unified minimal (4D) model of
spiking, seizures and spreading depression
−60 −40 −20 0 20 40
˜Ke / (mM/l)
−80
−60
−40
−20
0
20
40
mV
HB1
LP1
HB2
LP2
HB3
HB4
LP1lc
LP2lc
LP3lc
LP4lc
membrane potential for simple model
−60 −40 −20 0 20 40
˜Ke / (mM/l)
0
10
20
30
40
50
60
mM/l
HB1
LP1HB2
LP2
HB3
HB4
LP1lc
LP2lc
LP3lc
LP4lc
extrac. potassium for simple model
stable FP
unstable FP
stable LC
unstable LC
−49 −47 −45 −43
HB3
LP1lc
27 29 31
HB1
0.00 0.03
+2.87×101
HB1
PD LP5lc
LP6lc
−49 −47 −45 −43
HB3
LP1lc
27 29 31
LP1
LP3lc
5 10 15 20
Kbath / (mM/l)
20
40
60
80
100
120
140
160
mM/l
LP1
LP2
HB1
HB2
HB3
HB4
LP1lc
LP2lc
TR1
TR2
TR3
TR4
extrac. sodium
5 10 15 20
Kbath / (mM/l)
−80
−60
−40
−20
0
20
40
mM/l
LP1
LP2
HB1
HB2 HB3
HB4
LP1lc
LP2lc
TR1
TR2
TR3
TR4
potassium gain/loss ˜Ke
stable FP
unstable FP
stable LC
unstable LC
stable torus
6.7 6.9 7.1
HB1 TR4
PD

28. Slow–fast analysis using ˜K+
gain–and–loss
−80
−60
−40
−20
0
HB1
LP1
HB2
LP2
HB3
HB4
LP1lc
LP2lc
LP3lc
LP4lc
potential
(transmem.)
−60 −40 −20 0 20 40
0
10
20
30
40
50
60
HB1
LP1HB2
LP2
HB3
HB4
LP1lc
LP2lc
LP3lc
LP4lc
particle exchange (potassium ions)
potassium
(extracell.)
mM
mMmV
Open systems yield some
Ke dynamics:
dKe
dt
= ...
Ke can be subsituted by ˜Ke
(alternative formulation)
d ˜Ke
dt
= λ(Kbath − Ke )
with
Ke = K0
e + ωi
ωe
(K0
i − Ki ) + ˜Ke

29. The “migraine–aura–ischemic–stroke” cycle
−80
−60
−40
−20
0
HB1
LP1
HB2
LP2
HB3
HB4
LP1lc
LP2lc
LP3lc
LP4lc
potential
(transmem.)
−60 −40 −20 0 20 40
0
10
20
30
40
50
60
HB1
LP1HB2
LP2
HB3
HB4
LP1lc
LP2lc
LP3lc
LP4lc
particle exchange (potassium ions)
potassium
(extracell.)
mM
mMmV

30. The “migraine–aura–ischemic–stroke” cycle
−80
−60
−40
−20
0
HB1
LP1
HB2
LP2
HB3
HB4
LP1lc
LP2lc
LP3lc
LP4lc
potential
(transmem.)
−60 −40 −20 0 20 40
0
10
20
30
40
50
60
HB1
LP1HB2
LP2
HB3
HB4
LP1lc
LP2lc
LP3lc
LP4lc
particle exchange (potassium ions)
potassium
(extracell.)
mM
mMmV
trans-
membrane
events

31. The “migraine–aura–ischemic–stroke” cycle
−80
−60
−40
−20
0
HB1
LP1
HB2
LP2
HB3
HB4
LP1lc
LP2lc
LP3lc
LP4lc
potential
(transmem.)
−60 −40 −20 0 20 40
0
10
20
30
40
50
60
HB1
LP1HB2
LP2
HB3
HB4
LP1lc
LP2lc
LP3lc
LP4lc
particle exchange (potassium ions)
potassium
(extracell.)
mM
mMmV
++
iso-
intracellular
concentration

32. The “migraine–aura–ischemic–stroke” cycle
−80
−60
−40
−20
0
HB1
LP1
HB2
LP2
HB3
HB4
LP1lc
LP2lc
LP3lc
LP4lc
potential
(transmem.)
−60 −40 −20 0 20 40
0
10
20
30
40
50
60
HB1
LP1HB2
LP2
HB3
HB4
LP1lc
LP2lc
LP3lc
LP4lc
particle exchange (potassium ions)
potassium
(extracell.)
mM
mMmV
++

33. The “migraine–aura–ischemic–stroke” cycle
−80
−60
−40
−20
0
HB1
LP1
HB2
LP2
HB3
HB4
LP1lc
LP2lc
LP3lc
LP4lc
potential
(transmem.)
−60 −40 −20 0 20 40
0
10
20
30
40
50
60
HB1
LP1HB2
LP2
HB3
HB4
LP1lc
LP2lc
LP3lc
LP4lc
particle exchange (potassium ions)
potassium
(extracell.)
mM
mMmV
++
release of
Gibbs free
energy
Open question:
Can we treat this cycle in
analogy to a steam engine?

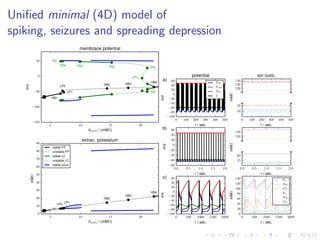
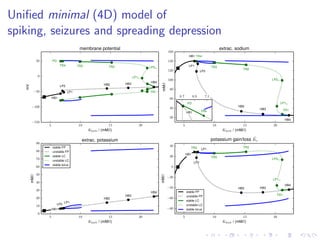
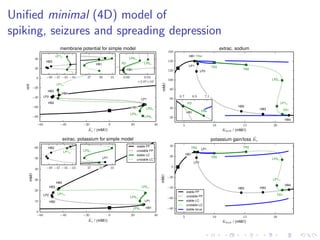
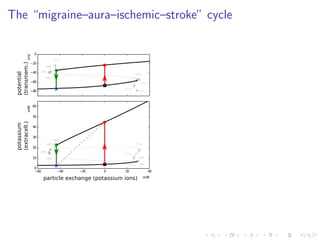
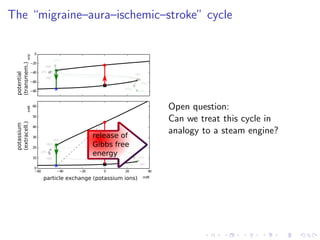
34. The “ceiling level” of [K+
]e in seizure activity
−80
−60
−40
−20
0
HB1
LP1
HB2
LP2
HB3
HB4
LP1lc
lc
lc
LP4lc
potential
(transmem.)
−60 −40 −20 0 20 40
0
10
20
30
40
50
60
HB1
LP1HB2
LP2
HB3
HB4
LP1lc
LP4lc
particle exchange (potassium ions)
potassium
(extracell.)
mM
mMmV
LP2
LP3
LP2lc
LP3lc
seizure-like
activity
"ceiling level"

35. Outline
Introduction
Unifying ion dynamics in the brain
Application: From genotype to phenotype
Summary

36. From genotype to cellular phenotype (just the recipe)
Tail currents to HH parameters:
120 80 40 0 40
V / mV
5
10
15
20
τ/ms
wild-type
mutant
0
1−1
e
1
h
deinactivation
0 10t / ms
120
10
V / mV
0
1
e
1
h
inactivation
0 10t / ms
120
10
V / mV
τ ∗
hτh τ ∗
hτh
Reduced firing rate!
0 20 40 60 80 100 120 140 160 180
Iapp / µA cm−2
0
50
100
150
200
wild-type
mutant
lower fire rate =
hypoexcitable
in rate-based
population models
F()/HzIapp
More susceptible to migraine
0 20 40 60 80 100
t / s
140
100
60
20
20
60
V/mV
mutant
V
EK
ENa
20%
100%
0 20 40 60 80 100
t / s
140
100
60
20
20
60
V/mV
wild-type
V
EK
ENa
20%
100%
13.6s
7.2s
• M.A. Dahlem, J. Schumacher, N H¨ubel, Linking a genetic defect in migraine to spreading depression in a
computational model (submitted arXiv 1403.6801)

37. Outline
Introduction
Unifying ion dynamics in the brain
Application: From genotype to phenotype
Summary

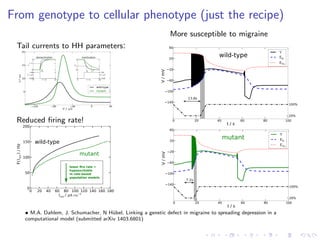
38. Conclusions
Including ion dynamics into a Hodghin-Huxley framework
yields slow quasiperodic dynamics:
important bifurcation parameter is gain–and–loss of ions,
explain the “ceiling level” of [K+
]e in seizure activity,
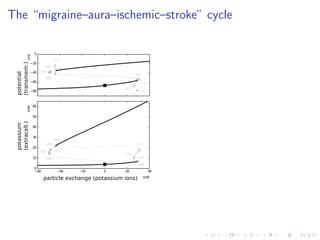
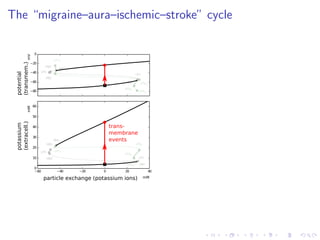
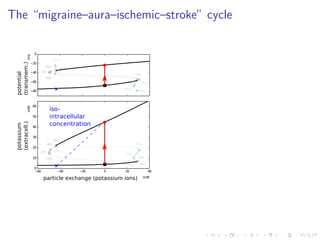
explain the “migraine–aura–ischemic–stroke” contiuum.
No synaptic currents needed for slow dynamics, in particular,
no metabotropic receptor that acts through a secondary
messenger, like GABAB.
Remark : Ultra–slow (or near–DC (direct current)) activity
that cannot be observed by electroencephalography (EEG),
because it is susceptible to uncontrollable artifacts such as
changes in the resistance of the dura.
However : subdural electrode recordings provided recently
direct and unequivocal evidence that such dynamics occurs in
abundance in people with structural brain damage.

39. Cooperation & Funding
Niklas H¨ubel, Julia Schumacher,
Thomas Isele
Steven Schiff
(Penn State Center for Neural Engineering)
Jens Dreier
(Department of Neurology, Charit´e; University Medicine, Berlin)
berlin
Migraine Aura Foundation