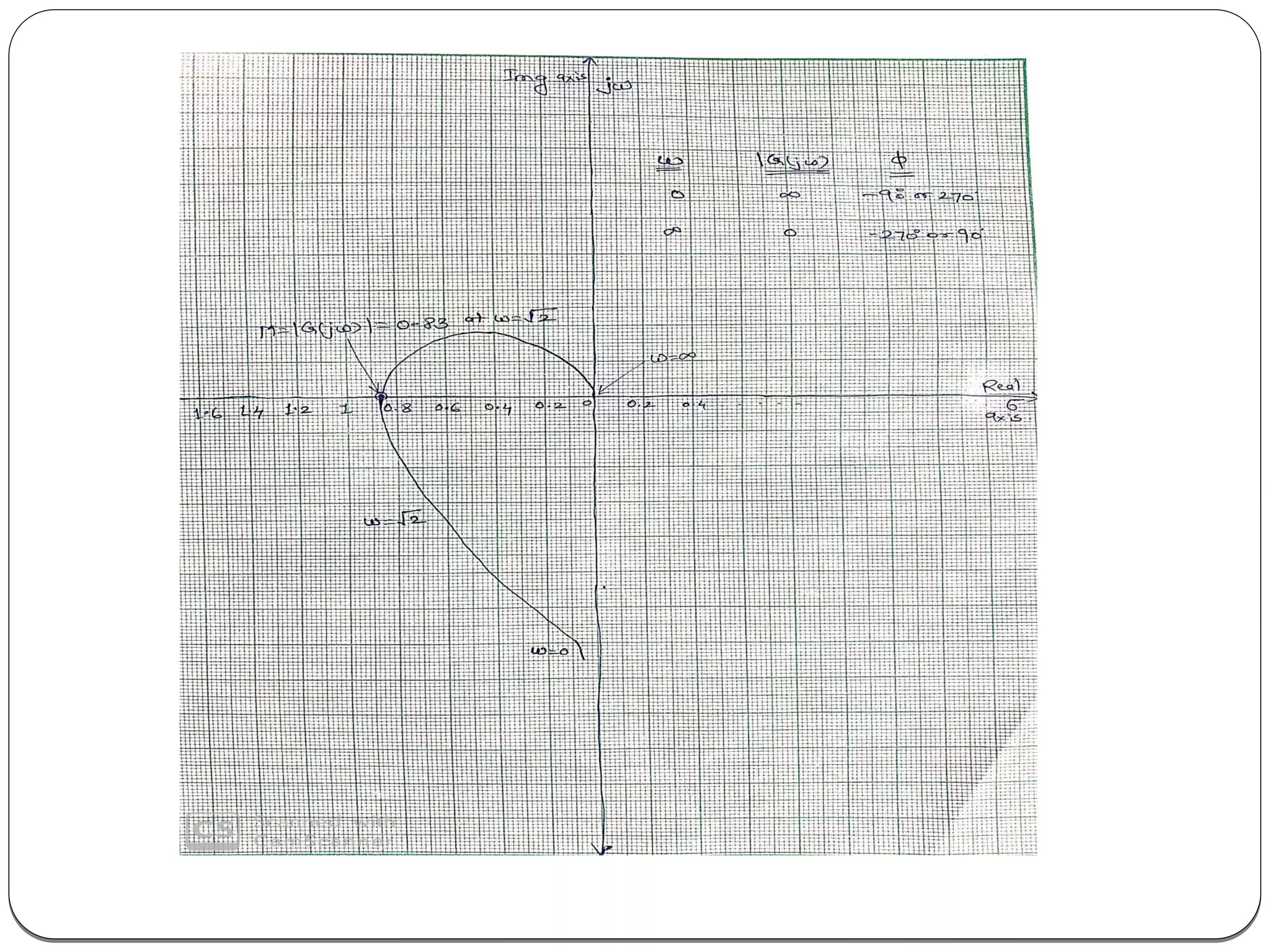
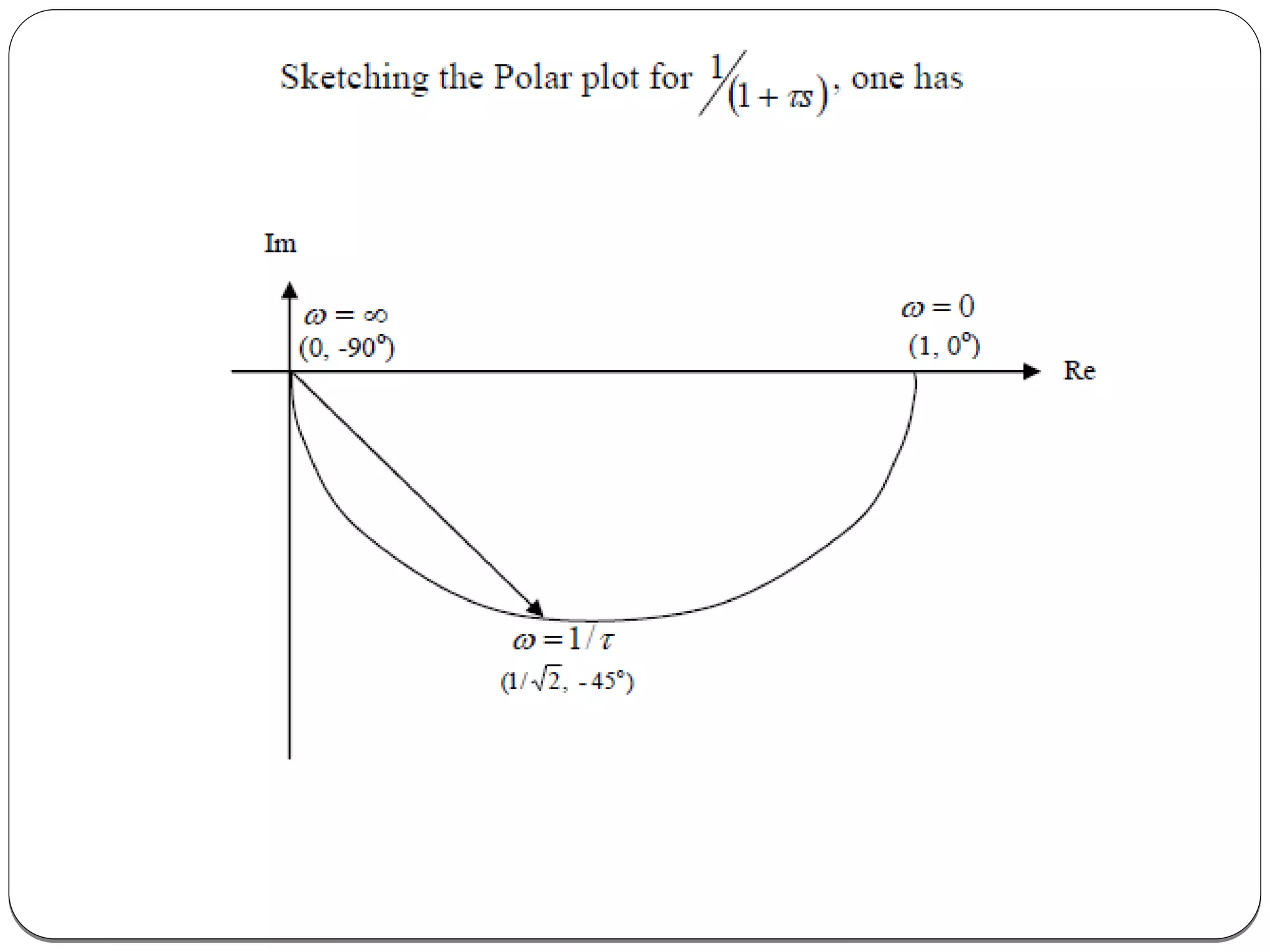
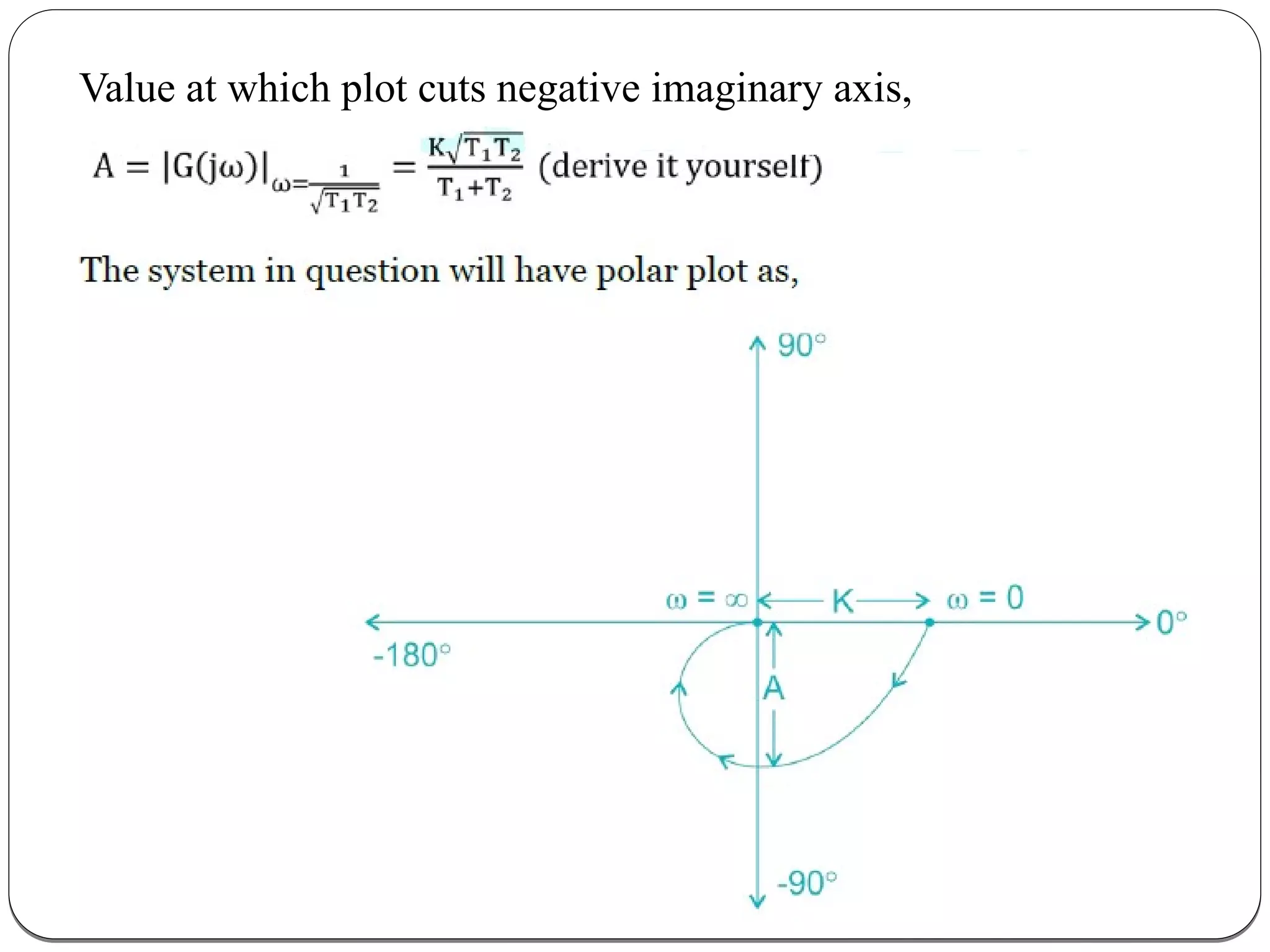
The document discusses polar plots, which graph the magnitude and phase of a transfer function G(jω)H(jω) as ω varies from 0 to infinity. It provides rules for drawing polar plots, such as substituting s=jω into the transfer function, finding the starting and ending magnitude and phase, and checking for intersections with the real and imaginary axes. An example is shown of creating a polar plot for a first order system, including determining the magnitude and phase expressions and values at specific ω points and drawing the resulting plot.

1. Polar plot
-By Prof. Mrunal

2. The polar form of G(jω)H(jω) is-
G(jω)H(jω)=|G(jω)H(jω)| G(jω)H(jω)∠
The Polar plot is a plot, which can be drawn between the magnitude and the
phase angle of G(jω)H(jω) by varying ω from zero to ∞. The polar graph sheet or
in a regular graph sheet is shown in the following figure.
Polar plot

3. Rules for Drawing Polar Plots:
Follow these rules for plotting the polar plots.
•Substitute, s=jω in the open loop transfer function.
•Write the expressions for magnitude and the phase of G(jω)H(jω).
•Find the starting magnitude and the phase of G(jω)H(jω) by substituting ω=0. So,
the polar plot starts with this magnitude and the phase angle.
•Find the ending magnitude and the phase of G(jω)H(jω) by substituting ω=∞. So,
the polar plot ends with this magnitude and the phase angle.
•Check whether the polar plot intersects the real axis, by making the imaginary
term of G(jω)H(jω) equal to zero and find the value(s) of ω.
•Check whether the polar plot intersects the imaginary axis, by making real term
of G(jω)H(jω) equal to zero and find the value(s) of ω.
•For drawing polar plot more clearly, find the magnitude and phase
of G(jω)H(jω) by considering the other value(s) of ω

4. Example
Consider the open loop transfer function of a closed loop control system.
Let us draw the polar plot for this control system using the above rules.
Step 1 − Substitute, s=jω in the open loop transfer function.
Step 2 -The magnitude of the open loop transfer function is
Step 3--The phase angle of the open loop transfer function is

5. Step 4 − The following table shows the magnitude and the phase angle of the open
loop transfer function at ω=0 rad/sec and ω=∞ rad/sec.
Step 5 − Separate real and imaginary part
we will get the ω value as √2.
Step 6 − substituting ω=√2
magnitude of the open loop transfer function M is-
M= |G(jω)|= 0.83
Step 7 - the polar plot with the above
information on the regular graph sheet is below.
Ste
p 1:
To divide complex numbers, you
must multiply by the conjugate.
To find the conjugate of a
complex number all you have to
do is change the sign between
the two terms in the denominator.
Ste
p 2:
Distribute (or FOIL) in both the
numerator and denominator to
remove the parenthesis.
Ste
p 3:
Simplify the powers of i,
specifically remember that i2
= –1.
Ste
p 4:
Combine like terms in both the
numerator and denominator, that
is, combine real numbers with
real numbers and imaginary
numbers with imaginary
numbers.
Ste
p 5:
Write you answer in the form a +
bi.
Ste
p 6: Reduce your answer if you can.
Here are the step require to
divide complex numbers:

7. Consider a first order system
where τ is the time constant.
Step 1 − Substitute, s=jω in the first order system.
Multiplying both numerator and denominator by the
conjugate of denominator
Step 2 -The magnitude of the transfer function is
Example

8. Step 3--The phase angle of the transfer function is
Step 4 Point Frequency (w) Magnitude Phase angle
1 0 1 0
2 ∞ 0 -90

9. For one more frequence point: Taking ω = 1/τ , then one has

11. Example

13. Value at which plot cuts negative imaginary axis,

14. Thank you