Downloaded 270 times
Uploaded byIzzati Hamid
Simplex method Big M infeasible
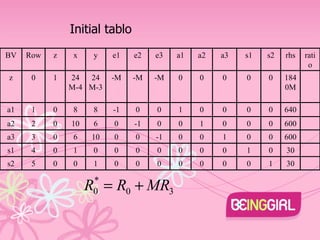
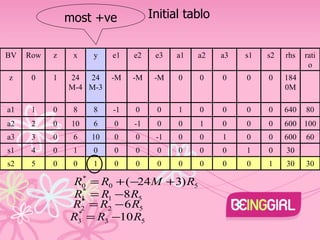
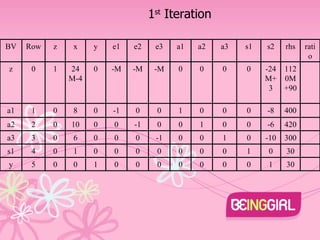
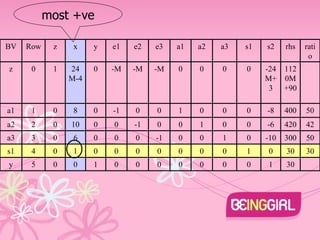
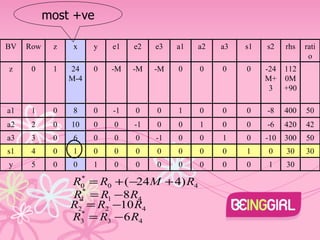
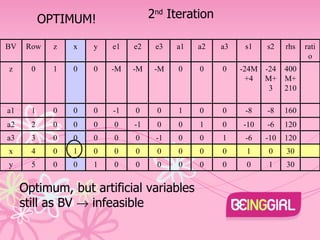
The document describes using the Big M method to solve a linear programming problem with the objective of minimizing z=4x+3y subject to multiple constraints on x and y. The problem is converted to standard form and an initial basic feasible solution is found with x=30, y=30, z=132. The simplex method is then used to iterate to the optimal solution with x=y=0, z=400.
More Related Content
Similar to Simplex method Big M infeasible
Simplex method Big M infeasible
- 1. The Big MMethod Minimize z = 4x + 3y Subject to 8x + 8y 640 10x + 6y 600 6x + 10y 600 x 30 y 30 x, y ≥ 0
- 2. z = 4x+ 3y + 0e 1 + 0e 2 + 0e 3 + 0s 1 + 0s 2 + Ma 1 + Ma 2 + Ma 3 8x + 8y – e 1 + a 1 = 640 10x + 6y – e 2 + a 2 = 600 6x + 10y – e 3 + a 3 = 600 x + s 1 = 30 y + s 2 = 30 x, y, e 1 , e 2 , e 3 , a 1 , a 2 , a 3 , s 1 , s 2 ≥ 0
- 3. z - 4x- 3y + 0e 1 + 0e 2 + 0e 3 + 0s 1 + 0s 2 - Ma 1 - Ma 2 - Ma 3 8x + 8y – e 1 + a 1 = 640 10x + 6y – e 2 + a 2 = 600 6x + 10y – e 3 + a 3 = 600 x + s 1 = 30 y + s 2 = 30 x, y, e 1 , e 2 , e 3 , a 1 , a 2 , a 3 , s 1 , s 2 ≥ 0
- 4. to make it0 BV Row z x y e1 e2 e3 a1 a2 a3 s1 s2 rhs ratio z 0 1 -4 -3 0 0 0 -M -M -M 0 0 0 a1 1 0 8 8 -1 0 0 1 0 0 0 0 640 a2 2 0 10 6 0 -1 0 0 1 0 0 0 600 a3 3 0 6 10 0 0 -1 0 0 1 0 0 600 s1 4 0 1 0 0 0 0 0 0 0 1 0 30 s2 5 0 0 1 0 0 0 0 0 0 0 1 30
- 5. to make it0 BV Row z x y e1 e2 e3 a1 a2 a3 s1 s2 rhs ratio z 0 1 8M-4 8M-3 -M 0 0 0 -M -M 0 0 640M a1 1 0 8 8 -1 0 0 1 0 0 0 0 640 a2 2 0 10 6 0 -1 0 0 1 0 0 0 600 a3 3 0 6 10 0 0 -1 0 0 1 0 0 600 s1 4 0 1 0 0 0 0 0 0 0 1 0 30 s2 5 0 0 1 0 0 0 0 0 0 0 1 30
- 6. to make it0 BV Row z x y e1 e2 e3 a1 a2 a3 s1 s2 rhs ratio z 0 1 18M-4 14M-3 -M -M 0 0 0 -M 0 0 1240M a1 1 0 8 8 -1 0 0 1 0 0 0 0 640 a2 2 0 10 6 0 -1 0 0 1 0 0 0 600 a3 3 0 6 10 0 0 -1 0 0 1 0 0 600 s1 4 0 1 0 0 0 0 0 0 0 1 0 30 s2 5 0 0 1 0 0 0 0 0 0 0 1 30
- 7. Initial tablo BVRow z x y e1 e2 e3 a1 a2 a3 s1 s2 rhs ratio z 0 1 24M-4 24M-3 -M -M -M 0 0 0 0 0 1840M a1 1 0 8 8 -1 0 0 1 0 0 0 0 640 a2 2 0 10 6 0 -1 0 0 1 0 0 0 600 a3 3 0 6 10 0 0 -1 0 0 1 0 0 600 s1 4 0 1 0 0 0 0 0 0 0 1 0 30 s2 5 0 0 1 0 0 0 0 0 0 0 1 30
- 8. Initial tablo most+ve BV Row z x y e1 e2 e3 a1 a2 a3 s1 s2 rhs ratio z 0 1 24M-4 24M-3 -M -M -M 0 0 0 0 0 1840M a1 1 0 8 8 -1 0 0 1 0 0 0 0 640 80 a2 2 0 10 6 0 -1 0 0 1 0 0 0 600 100 a3 3 0 6 10 0 0 -1 0 0 1 0 0 600 60 s1 4 0 1 0 0 0 0 0 0 0 1 0 30 s2 5 0 0 1 0 0 0 0 0 0 0 1 30 30
- 9. 1 st Iteration BV Row z x y e1 e2 e3 a1 a2 a3 s1 s2 rhs ratio z 0 1 24M-4 0 -M -M -M 0 0 0 0 -24M+3 1120M+90 a1 1 0 8 0 -1 0 0 1 0 0 0 -8 400 a2 2 0 10 0 0 -1 0 0 1 0 0 -6 420 a3 3 0 6 0 0 0 -1 0 0 1 0 -10 300 s1 4 0 1 0 0 0 0 0 0 0 1 0 30 y 5 0 0 1 0 0 0 0 0 0 0 1 30
- 10. most +ve BVRow z x y e1 e2 e3 a1 a2 a3 s1 s2 rhs ratio z 0 1 24M-4 0 -M -M -M 0 0 0 0 -24M+3 1120M+90 a1 1 0 8 0 -1 0 0 1 0 0 0 -8 400 50 a2 2 0 10 0 0 -1 0 0 1 0 0 -6 420 42 a3 3 0 6 0 0 0 -1 0 0 1 0 -10 300 50 s1 4 0 1 0 0 0 0 0 0 0 1 0 30 30 y 5 0 0 1 0 0 0 0 0 0 0 1 30
- 11. most +ve BVRow z x y e1 e2 e3 a1 a2 a3 s1 s2 rhs ratio z 0 1 24M-4 0 -M -M -M 0 0 0 0 -24M+3 1120M+90 a1 1 0 8 0 -1 0 0 1 0 0 0 -8 400 50 a2 2 0 10 0 0 -1 0 0 1 0 0 -6 420 42 a3 3 0 6 0 0 0 -1 0 0 1 0 -10 300 50 s1 4 0 1 0 0 0 0 0 0 0 1 0 30 30 y 5 0 0 1 0 0 0 0 0 0 0 1 30
- 12. 2 nd Iteration OPTIMUM! Optimum, but artificial variables still as BV infeasible BV Row z x y e1 e2 e3 a1 a2 a3 s1 s2 rhs ratio z 0 1 0 0 -M -M -M 0 0 0 -24M+4 -24M+3 400M+210 a1 1 0 0 0 -1 0 0 1 0 0 -8 -8 160 a2 2 0 0 0 0 -1 0 0 1 0 -10 -6 120 a3 3 0 0 0 0 0 -1 0 0 1 -6 -10 120 x 4 0 1 0 0 0 0 0 0 0 1 0 30 y 5 0 0 1 0 0 0 0 0 0 0 1 30