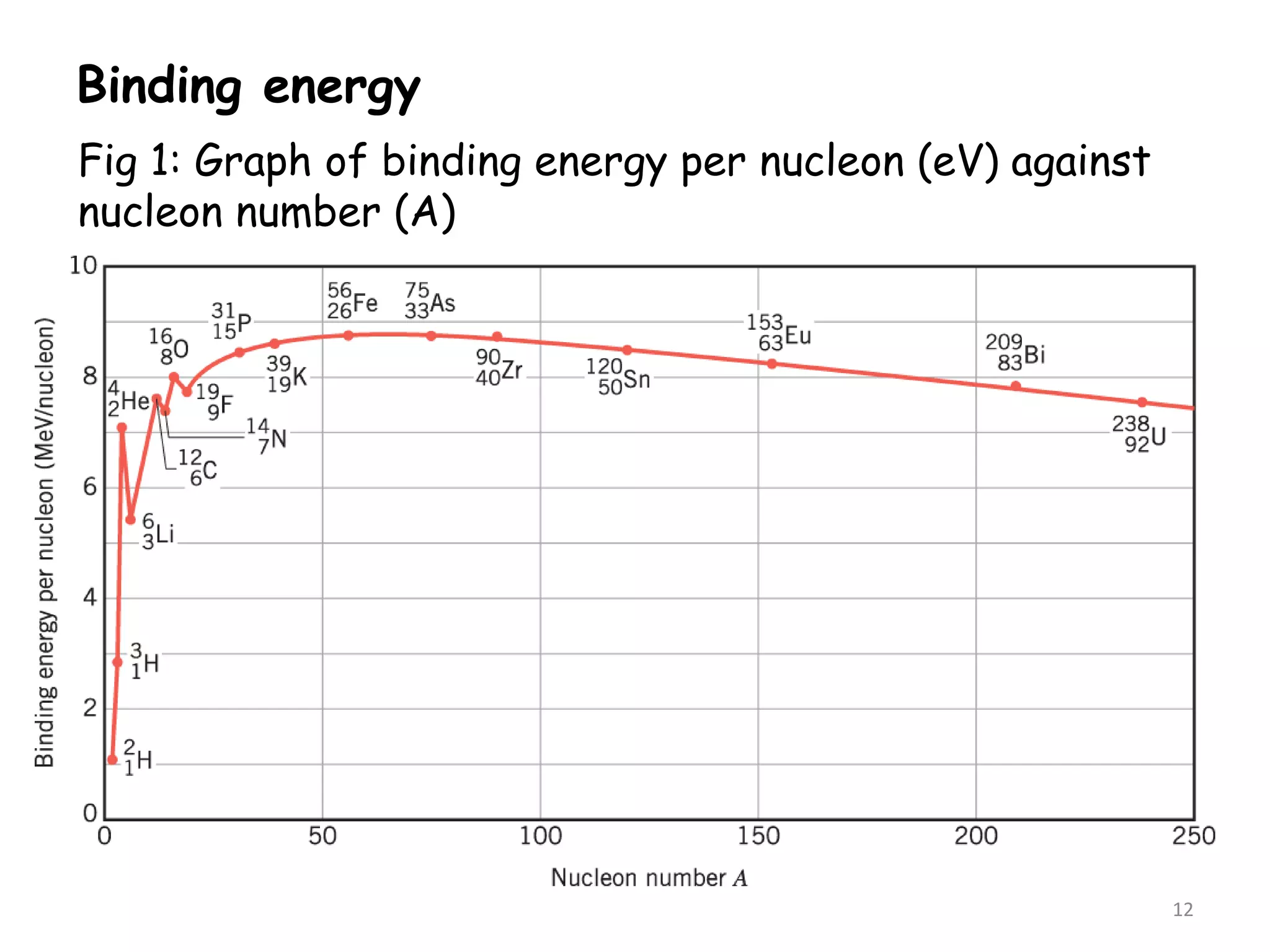
1. The mass defect for the helium nucleus is 0.03039 atomic mass units or 5.046×10−29 kg. This mass defect is equivalent to 4.54×10−12 J of energy needed to separate the nucleus according to Einstein's mass-energy equivalence formula. 2. The binding energy per nucleon is typically around 8 MeV and indicates the stability of the nucleus. More stable nuclei have higher binding energies per nucleon. During radioactive decay, the daughter nucleus is more stable and has a higher binding energy per nucleon than the parent nucleus. The energy released during decay comes from the mass defect between the parent and daughter nuclei. 3. Calculating the mass defect and applying Einstein

1. Nuclear Energy
Mass Defect
1

2. Introduction
• Nuclear power stations tap into the energy stored
inside an atom’s nucleus.
• Huge amounts of energy can be released.
• But where does it come from and how can we get at
it?
Learning Outcomes:
• At the end of this lesson you will be able to:
1. Explain Mass Defect
2. Calculate the energy stored by an atomic nucleus
2

3. Missing mass – Mass Defect
• A helium nucleus is made up of 2 protons and 2
neutrons.
• When the mass of two protons + mass of 2 neutrons
is compared with mass of helium nucleus – something
very odd is seen.
• The mass of the nucleus is less than the total mass of
the individual particles that it contains
• True for all nuclei containing more than one nucleon.
• Missing mass is known as mass difference or mass
defect.
• Masses involved are very small – measured in atomic
mass units u, where:
• 1u = 1.6605 x 10-27
kg
3

4. Mass defect
Mass
(atomic mass unit)
Proton 1.00728 u
Neutron 1.00867 u
Helium nucleus 4.00151 u
Table 1:
Atomic mass
units.
Example 1.
Using the data in table 1, calculate the mass defect for a
helium nucleus in atomic mass units and in kilograms.
Mass of 2p + 2n = (2 x 1.00728 u) + (2 x 1.00867 u)
= 4.03190 u
Mass defect = 4.03190 u – 4.00151 u = 0.03039 u
Mass defect in kg = 0.03039 x 1.6605 x 10-27
kg
= 5.046 x 10-29
kg
4

5. Mass defect
• A mass of 5.046 x 10-27
kg may not sound a lot – but on
atomic scale it is significant.
• The mass defect is about 3% of the mass of a proton
(or 55 electrons)
• It is important to measure nuclear masses precisely –
masses are quoted to 6 significant figures.
Mass and energy equivalence
• Splitting the nucleus into individual nucleons results in
increase of total mass.
• Where does this extra mass come from?
• Splitting the nucleus is very difficult – nucleons held
together by a very strong but short-range nuclear
forces.
• Overcoming these forces requires energy
5

6. Mass defect
• What happens to this energy?
• Energy disappears into the system and mass is
created!
• Goes against the conventional conservation laws.
6
Albert Einstein
It was Albert Einstein who
suggested that mass and energy
are equivalent.
He linked mass and energy in his
famous equation: E = m . c 2
E is the energy equivalent in joules
of a mass m in kilograms, c is the
velocity of light (3.00 x 108
m s-1
)

7. 7
Example 2:
Calculate the energy equivalent of the mass defect
calculated in Example 1.
E = m c2
= 5.046 x 10-29
kg x (3.00 x 108
m s-1
)2
= 4.54 x 10-12
J (3 s.f.)
This is the energy needed to separate the helium nucleus
into individual protons and neutrons.
42He + 4.54 x 10-12
J → 2p + 2n
energy
In any system, the total amount of mass and energy is
conserved.

8. Energy equivalent of 1 u
• Einstein’s equation uses mass in kg and energy in J.
• In nuclear physics we are more likely to be working in
atomic mass units (u) and electron-volts (eV)
• Need to work out energy equivalent (in eV) of 1 u:
• Using Einstein’s equation with a precise value for the
velocity of light:
• E = m c2
= 1.6605 x 10-27
kg x (2.9979 x 108
m s-1
)2
= 1.4924 x 10-10
J
• But 1 eV = 1.6022 x 10-19
J
• Hence E = 1.4924 x 10-10
J / 1.6022 x 10-19
= 9.315 x 108
eV = 931.5 x 106
eV
• 1 u = 931.5 MeV
8

9. 9
Example 3:
A carbon nucleus has a mass of 11.9967 u
How much energy, in MeV, would ne needed to split it
into its 6 protons and 6 neutrons?
(mp = 1.00728 u, mn = 1.00867 u)
Mass of 6p + 6 n = (6 x 1.00728 u) + (6 x 1.00867 u)
= 12.0957 u
Mass defect = 12.0957 u – 11.9967 u = 0.0990 u
Energy equivalent = 0.0990 x 931.5 MeV
= 92.2 MeV needed to separate the 12 nucleons.
Question:
Calculate the mass defect in u and kg for the following
nuclei:
(a)Lithium (7
3Li), nuclear mass = 7.014353 u
(b)Silicon (28
14Si), nuclear mass = 27.96924 u

10. Binding energy
• Energy needed to separate a nucleus into individual
nucleons is its binding energy.
• Also the energy equivalent of the mass defect –
found from E = m c2
• Binding energy indicates the stability of the nucleus.
• Total binding energy is linked to the size of the
nucleus.
• The more nucleons there are, the greater the energy
needed to separate them all out.
• More useful comparison is the binding energy per
nucleon.
• Average energy needed to remove each nucleon from
the nucleus.
10

11. 11
Example 4:
Use the figures calculated in example 3 to find the
binding energy per nucleon for a carbon-12 nucleus.
Carbon-12 contains 12 nucleons (6p + 6n)
Total binding energy for carbon-12 = 92.2 MeV
Binding energy per nucleon = 92.2 MeV / 12
= 7.68 MeV
Question
For each of the two nuclei in question on slide 9, calculate:
(a)Total binding energy in eV
(b)The binding energy per nucleon in eV

12. Binding energy
12
Fig 1: Graph of binding energy per nucleon (eV) against
nucleon number (A)

13. Binding energy
• Notice that binding energy per nucleon is typically
around 8 MeV
• The most stable nucleus has the highest binding
energy per nucleon.
• This is 8.79 MeV for 56
26Fe
Radioactive Decay and Binding Energy
• Unstable nucleus emits radiation and becomes more
stable.
• Daughter nucleus always has a higher binding energy
per nucleon than the parent.
• Energy is given out when a nucleus decays
• Where does it come from?
13

14. Radioactive Decay and Binding Energy
• Total mass of products is less than mass of parent
nucleus.
• Mass difference is released as energy – look at the
following examples:
Example 5: α-decay
• Thorium-228 decays by α-emission:
228
90Th → 224
88Ra + 4
2α
• Mass of thorium-228 nucleus = 227.97929 u
• Mass of radium-224 nucleus + α-particle
= 223.97189 u + 4.00151 u = 227.97240 u
Mass difference = 227.97929 u – 227.97340 u
= 0.00589 u = 5.49 MeV (as 1 u = 931.5 MeV)
14

15. Radioactive Decay and Binding Energy
• The surplus energy appears mostly as K.E. of the α-
particle.
• Radium nucleus also recoils slightly (momentum is
conserved).
Example 6: β-decay
• Aluminium-29 decays by β-emission
15
29
13Al → 29
14Si + 0
-1β + 0
0ν-
Mass of Si-29 nucleus + β-particle + antineutrino
= 28.96880 u + 0.000549 u + 0 = 28.969349 u
Mass of aluminium-29 nucleus = 28.97330 u
Mass difference = 28.97330 u – 28.960349 u = 0.003951 u
= 3.68 MeV (as 1 u = 931.5 MeV)

16. Radioactive Decay and Binding Energy
• Some of this energy is carried away by a γ-ray.
• Rest becomes KE of the decay products.
Transmutation and energy
• Transmutation is conversion of one element to
another
• Radioactive decay is a spontaneous transmutation
with a release of energy.
• Some elements can be made by firing very fast
moving charged particles at a stable nucleus –
artificial transmutation. (energy must be supplied)
• First achieved by Rutherford, Marsden and Chadwick
in 1919.
16

17. Transmutation and energy
• Converted nitrogen into oxygen by bombarding it with
α-particles.
14
7N + 4
2α → 17
8O + 1
1H
• Here mass of products is greater.
• Energy must be supplied to make this reaction happen
and balance the nuclear equation
• Energy comes from K.E. of the α-particle. Modern use
of artificial transmutation is the production of
medical radioisotopes.
Questions
1. The decay of radium into radon is
226
88Ra → 222
86Rn + 4
2
α
calculate the energy released in eV 17

18. Questions
18
2. A possible reaction for the fission of uranium is:
235
92U + 1
0n → 146
57La + 87
35Br + 31
0n
Calculate the energy released in the reaction in MeV.
3. Calculate the minimum energy needed in MeV to make
the following reaction happen:
60
28Ni + 4
2α → 63
30Zn + 1
0n
Nuclear masses: radium-226 = 225.9771 u
radon-222 = 221.9703 u
uranium-235 = 234.9934 u
lanthanum-146 = 145.8684 u
bromine-87 = 86.9153 u
nickel-60 = 59.9153 u
zinc-63 = 62.9205 u