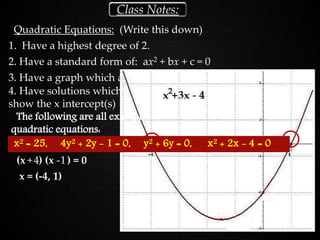
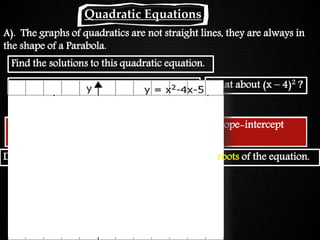
This document provides notes and examples on solving quadratic equations. It begins with an agenda for the day which includes warm up exercises, class notes on solving quadratics, and a factoring test. The class notes section defines quadratic equations, explains their standard form and graph as a parabola, and provides examples of solving various quadratics by factoring. It also discusses properties of parabolas such as having two solutions. The document concludes by providing examples and steps for solving different types of quadratics by factoring and taking square roots.

1. Today:
 Warm Up
 Class Notes; Solving Quadratic Equations
 Questions from Class Work??
 Factoring Test

2. Factoring (ax2
+ bx + c) Trinomials
Factor 5x4y –
80x2y3
Warm Up/Test Review
Factor 5x – 5y + ax -
ay
Factor 16x2 – 8xy + y2
2𝑥2
+ 19𝑥 + 24

3. Quadratic Equations: (Write this down)
Class Notes:
1. Have a highest degree of 2.
2. Have a standard form of: ax2 + bx + c = 0
3. Have a graph which always results in a parabola.
4. Have solutions which
show the x intercept(s)
Solve: x2 + 3x - 4 = 0
(x ) (x ) = 0+ -4 1
x = (-4, 1)
x2 = 25, 4y2 + 2y - 1 = 0, y2 + 6y = 0, x2 + 2x - 4 = 0
The following are all examples of
quadratic equations:

4. A). The graphs of quadratics are not straight lines, they are always in
the shape of a Parabola.
B) Parabolas ALWAYS have two solutions.
C) The slope of a quadratic is not constant. The slope-intercept
formula will not work with parabolas.
What about (x – 4)2
?
These are referred to as repeated solutions.
Find the solutions to this quadratic equation.
D) The solutions of a equation are also called the roots of the equation.
Quadratic Equations

5. Parabolas: ...In Sports

6. Parabolas: ...In Archeticture

7. Parabolas: ...In Nature

8. Parabolas: ...Everywhere
And, of course, the most important Parabola of all

9. Solving Quadratic Equations by Factoring
Let's look at some of the different types of equations
you'll face and how to deal with each of them
1: Set the equation = to 0 and solve:
Example A. x2 + 6x + 9
x2 + 6x + 9 = 0; (x + 3) (x + 3) = 0, x = -3.This is a perfect square
trinomial, and the parabola only touches the x axis at -3 and
would be in this shape:
-3

11. Solving Quadratic Equations by Factoring
2. Solve x2 = 64. Remember the standard form?
ax2 + bx + c = 0, where only a cannot = 0
In this case, b is 0, and c is 64.
We can solve by taking the square root of both sides.
3. Solve: 2x2 - x = 3
Place all terms to the left of the = sign (Standard Form).
The result is x = + 8; x = 8, and x = -8
4. Solve: x2 = 5x ***Do not cancel an 'x' from each side.
Factor GCF first, then solve

12. Take 5, then we'll begin the test:
Please Clear Your Desks/Tables of everything
Except scratch paper, pencil, calculator.
 You will need:
 Your correct code, pencil only, no phones.,
scratch paper
 You can use a regular calculator, but one is
not necessary for this test.

13. V.4, Question # 8