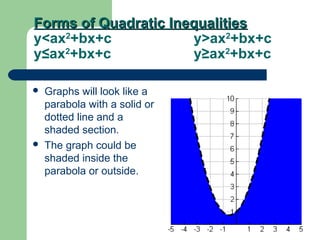
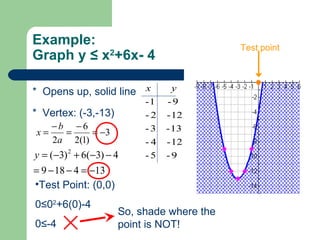
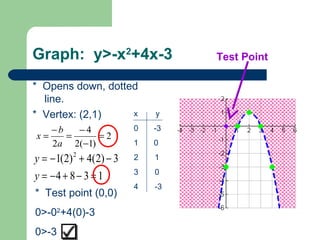
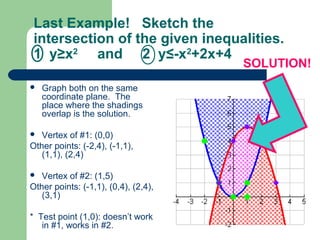
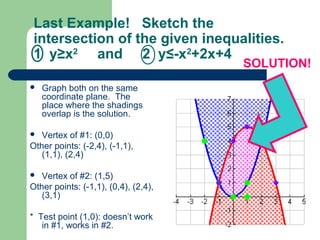
Graphs of quadratic inequalities will be parabolas with solid or dotted lines and shaded regions above or below the parabola. To graph: 1) sketch the parabola y=ax^2+bx+c, 2) choose a test point and see if it satisfies the inequality, 3) shade the appropriate region based on the test point. For example, to graph y ≤ x^2+6x-4: the parabola opens up with a solid line and vertex at (-3,-13), the test point (0,0) satisfies the inequality so shade below the parabola.

1. 5.8 Graphs of Quadratic
Inequalities
p. 312

2. Forms of Quadratic Inequalities
y<ax2+bx+c
y>ax2+bx+c
y≤ax2+bx+c
y≥ax2+bx+c


Graphs will look like a
parabola with a solid or
dotted line and a
shaded section.
The graph could be
shaded inside the
parabola or outside.

3. Steps for graphing
1. Sketch the parabola y=ax2+bx+c
(dotted line for < or >, solid line for ≤ or ≥)
** remember to use 5 points for the graph!
2. Choose a test point and see whether it is a
solution of the inequality.
3. Shade the appropriate region.
(if the point is a solution, shade where the
point is, if it’s not a solution, shade the other
region)

4. Example:
Graph y ≤ x2+6x- 4
* Opens up, solid line x
* Vertex: (-3,-13)
−b −6
x=
=
= −3
2a 2(1)
y = (−3) 2 + 6(−3) − 4
= 9 − 18 − 4 = −13
•Test Point: (0,0)
0≤02+6(0)-4
0≤-4
-1
-2
-3
-4
-5
Test point
y
-9
- 12
- 13
- 12
-9
So, shade where the
point is NOT!

5. Graph: y>-x2+4x-3
* Opens down, dotted
line.
x
* Vertex: (2,1)
y
−b
−4
x=
=
=2
2a 2(−1)
0
-3
1
0
y = − 1(2) 2 + 4(2) − 3
y = −4 + 8 − 3 = 1
2
1
3
0
4
-3
* Test point (0,0)
0>-02+4(0)-3
0>-3
Test Point

6. Last Example! Sketch the
intersection of the given inequalities.
1 y≥x2 and 2 y≤-x2+2x+4
SOLUTION!

Graph both on the same
coordinate plane. The
place where the shadings
overlap is the solution.
Vertex of #1: (0,0)
Other points: (-2,4), (-1,1),
(1,1), (2,4)

Vertex of #2: (1,5)
Other points: (-1,1), (0,4), (2,4),
(3,1)

* Test point (1,0): doesn’t work
in #1, works in #2.

7. Last Example! Sketch the
intersection of the given inequalities.
1 y≥x2 and 2 y≤-x2+2x+4
SOLUTION!

Graph both on the same
coordinate plane. The
place where the shadings
overlap is the solution.
Vertex of #1: (0,0)
Other points: (-2,4), (-1,1),
(1,1), (2,4)

Vertex of #2: (1,5)
Other points: (-1,1), (0,4), (2,4),
(3,1)

* Test point (1,0): doesn’t work
in #1, works in #2.