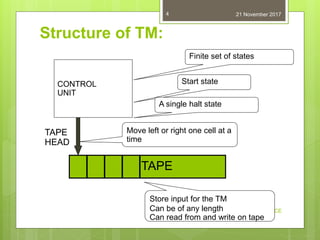
A Turing machine is a mathematical model of computation that consists of an infinite tape divided into cells, a head that reads and writes symbols on the tape, and a finite set of states. Alan Turing invented the Turing machine in 1936 to formalize the idea of algorithmic computation. A Turing machine operates by reading a symbol from the tape according to its transition function, then writing a symbol, changing its state, and moving the head left or right. If the machine reaches an accepting state, the input is accepted, otherwise it is rejected.

1. TURING
MACHINES
(TM)
-Sampath Kumar S,
AP/CSE, SECE

2. TURING MACHINES- Introduction
 A Turing Machine is an accepting device which accepts the
languages (recursively enumerable set) generated by type 0
grammars.
 It was invented in 1936 by Alan Turing.
 A Turing Machine (TM) is a mathematical model which
consists of an infinite length tape divided into cells on which
input is given.
 It consists of a head which reads the input tape.
 A state register stores the state of the Turing machine. After
reading an input symbol, it is replaced with another symbol,
its internal state is changed, and it moves from one cell to the
right or left.
 If the TM reaches the final state, the input string is accepted,
otherwise rejected.
21 November 2017
Sampath Kumar S, AP/CSE, SECE
2

3. Sampath Kumar S, AP/CSE, SECE
3
What does a TM do?
Determine if an input x is in a
language.
Eg: Answer if the answer of a problem P
for the instance x is “yes”.
Compute a function
Eg: Given an input x, what is f(x)?
21 November 2017

4. Sampath Kumar S, AP/CSE, SECE
4
Structure of TM:
CONTROL
UNIT
TAPE
TAPE
HEAD
Finite set of states
Move left or right one cell at a
time
Store input for the TM
Can be of any length
Can read from and write on tape
Start state
A single halt state
21 November 2017

5. Comparison with the previous
automation
 The following table shows a comparison of how a
Turing machine differs from Finite Automaton and
Pushdown Automaton.
21 November 2017
Sampath Kumar S, AP/CSE, SECE
5
Machine Storage Deterministic
Finite Automaton NO Yes
Pushdown Automaton Stack No
Turing Machine Infinite Tape Yes

6. How does a TM work?
 At the beginning,
TM is in the start state (initial state)
Its tape head points at the first cell
The tape contains , following by
input string, and the rest of the tape
contains .
21 November 2017
Sampath Kumar S, AP/CSE, SECE
6

7. How does a TM work?
For each move, a TM
 Reads the symbol under its tape head
 According to the transition function on the
symbol read from the tape and its current
state, the TM:
 Write a symbol on the tape
 Move its tape head to the left or right one cell or
not
 Changes its state to the next state
21 November 2017
Sampath Kumar S, AP/CSE, SECE
7

8. Sampath Kumar S, AP/CSE, SECE
8
When does a TM stop working?
 TM stops working,
 When it gets into the special state called
halt state (halts).
 The output of the TM is on the tape.
 when the tape head is on the leftmost cell
and is moved to the left. (hangs)
 when there is no next state. (hangs)
21 November 2017

9. Definition of Turing Machine:
A TM can be formally described as a 7-tuple (Q, ∑, Γ δ,
q0, B, F) where −
 Q: finite set of states
 ∑: finite set of input alphabet
 Γ: tape alphabet which always include blank symbol.
 δ: transition function;
δ : Q × Γ → Q × Γ × {Left_shift, Right_shift}.
 q0: the initial state (q0 ∈ Q)
 B : the blank symbol
 F: a set of the final state (F ⊆ Q)
21 November 2017
Sampath Kumar S, AP/CSE, SECE
9

10. 21 November 2017
Sampath Kumar S, AP/CSE, SECE
11

11. நன்றி
21 November 2017
Sampath Kumar S, AP/CSE, SECE
12