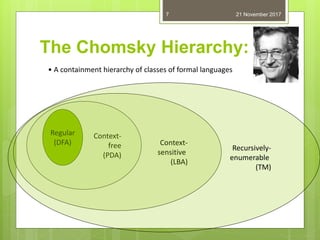
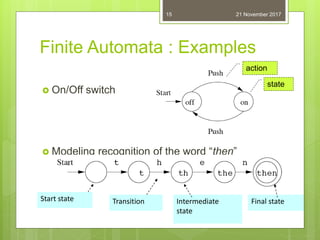
The document introduces automata theory, focusing on abstract computing devices called automata and their historical significance, particularly the contributions of Alan Turing and the development of the Chomsky hierarchy. It explains the fundamentals of languages, grammars, and finite state machines, including their classifications into deterministic and non-deterministic types. The applications of finite automata in various fields such as digital circuits, compilers, and pattern recognition are also discussed.

1. Introduction
to Automata
Theory
-Sampath Kumar S,
AP/CSE, SECE

2. What is Automata Theory?
 Study of abstract computing devices, or
“machines”.
 Automaton = an abstract computing device
 Note: A “device” need not even be a physical
hardware!
 A fundamental question in computer science:
 Find out what different models of machines can do
and cannot do
 The theory of computation
 Computability vs. Complexity
2 21 November 2017

3. What is Automata ?
 The term "Automata" is derived from the
Greek word "αὐτόματα" which means "self-
acting".
 An automaton (Automata in plural) is an
abstract self-propelled computing device
which follows a predetermined sequence of
operations automatically.
Abstract: Existing in thought or as
an idea but not having a physical
or concrete existence.
21 November 20173

4. Alan Turing (1912-1954)
 Father of Modern Computer
Science
 British mathematician
 Studied abstract machines called
Turing machines even before
computers existed
 Heard of the Turing test?
4 21 November 2017

5. Theory of Computation: A
Historical Perspective
5
1930s • Alan Turing studies Turing machines
• Decidability
• Halting problem
1940-1950s
• “Finite automata” machines studied
• Noam Chomsky proposes the
“Chomsky Hierarchy” for formal
languages
1969
Cook introduces “intractable” problems
or “NP-Hard” problems
1970-
Modern computer science: compilers,
computational & complexity theory evolve
21 November 2017

6. Languages & Grammars
 Languages: “A language is a
collection of sentences of
finite length all constructed
from a finite alphabet of
symbols”
 Grammars: “A grammar can
be regarded as a device that
enumerates the sentences of
a language” - nothing more,
nothing less
 N. Chomsky, Information and
Control, Vol 2, 1959
6
Or “words”
Image source: Nowak et al. Nature, vol 417, 2002
21 November 2017

7. The Chomsky Hierarchy:
7
Regular
(DFA)
Context-
free
(PDA)
Context-
sensitive
(LBA)
Recursively-
enumerable
(TM)
• A containment hierarchy of classes of formal languages
21 November 2017

8. Finite State Machine:
 An automaton with a finite number of states is
called a Finite Automaton(FA) or Finite State
Machine (FSM).
21 November 20178

9. Formal definition of a FSA:
An automaton can be represented by a 5-tuple (Q, ∑,
δ, q0, F), where −
 Q is a finite set of states.
 ∑ is a finite set of symbols, called the alphabet of
the automaton.
 δ is the transition function.
 q0 is the initial state from where any input is
processed (q0 ∈ Q).
 F is a set of final state/states of Q (F ⊆ Q).
Note: δ is called Delta and ∑ is called Sigma
21 November 20179

10. Finite Automaton classification:
Finite Automaton can be classified into two types −
 Deterministic Finite Automaton (DFA)
 Non-deterministic Finite Automaton (NDFA / NFA)
21 November 201714

11. Finite Automata : Examples
 On/Off switch
 Modeling recognition of the word “then”
15
Start state Final stateTransition Intermediate
state
action
state
21 November 2017

12. Finite Automata
 Some Applications
 Software for designing and checking the
behavior of digital circuits
 Lexical analyzer of a typical compiler
 Software for scanning large bodies of text (e.g.,
web pages) for pattern finding
 Software for verifying systems of all types that
have a finite number of states (e.g., stock
market transaction, communication/network
protocol)
16 21 November 2017

13. 21 November 201718

14. நன்றி
21 November 201719