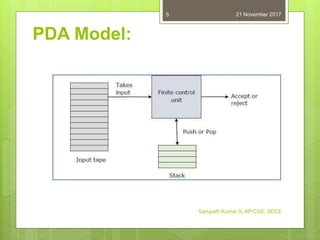
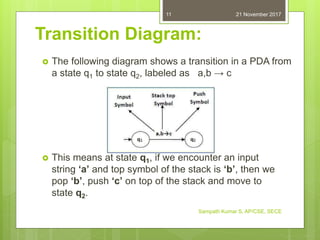
A pushdown automaton (PDA) is a type of finite state machine that uses a stack to remember an infinite amount of information. A PDA has three components: an input tape, a control unit, and a stack with infinite size. It can perform two stack operations - push, which adds a new symbol to the top of the stack, and pop, which reads and removes the top symbol. A PDA is formally defined as a 7-tuple that specifies its states, alphabets, transition function, initial state, initial stack symbol, and accepting states. A PDA accepts a language either by entering an accepting state after consuming the input string or by having an empty stack when reading is complete.

1. Pushdown
Automata (PDA)
-Sampath Kumar S,
AP/CSE, SECE

2. Pushdown Automata - Introduction
 A pushdown automaton is a way to implement a
Context - Free Grammar in a similar way we
design DFA for a regular grammar.
 A DFA can remember a finite amount of
information, but a PDA can remember an infinite
amount of information.
 Basically a pushdown automaton is −
"Finite state machine" + "a stack"
21 November 2017
Sampath Kumar S, AP/CSE, SECE
2

3. Components of PDA
A pushdown automaton has three components:
 An input tape
 A control unit and
 A stack with infinite size.
The stack head scans the top symbol of the stack.
21 November 2017
Sampath Kumar S, AP/CSE, SECE
3

4. Stack Operations
A stack does two operations −
 Push − A new symbol is added at the top.
 Pop − The top symbol is read and removed.
A PDA may or may not read an input symbol, but
it has to read the top of the stack in every
transition.
21 November 2017
Sampath Kumar S, AP/CSE, SECE
4

5. PDA Model:
21 November 2017
Sampath Kumar S, AP/CSE, SECE
5

6. Definition of PDA
A PDA can be formally described as a 7-tuple (Q, ∑,
Γ , δ, q0, Z0, F) −
 Q: a finite set of states
 ∑: a finite set of input alphabet
 Γ: a finite set of stack symbols
 δ: a transition function from
Q × (∑ ∪ {ε}) × Γ × Q × S*
 q0: the initial state (q0 ∈ Q)
 Z0: the initial stack top symbol (Z0 ∈ Γ)
 F: a set of the final state (F ⊆ Q)
21 November 2017
Sampath Kumar S, AP/CSE, SECE
6

7. Alphabets in PDA:
PDA has 2 alphabets:
 An input alphabet ∑ (input string)
 A stack alphabet Γ (stored on the stack)
21 November 2017
Sampath Kumar S, AP/CSE, SECE
7

8. Moves on PDA
A move on PDA may include
1. An element may be added (PUSH) to the stack.
2. An element may be deleted (POP) from the stack
(q, a, Z0) = (q, ε).
3. There may or may not be change of state.
21 November 2017
Sampath Kumar S, AP/CSE, SECE
8

9. Example of Moves on PDA
1. (q, a, Z0) = (q, aZ0) indicates that in the state q on
seeing a, a is pushed on to stack (placed on top
of Z0). There is no change of the state.
2. (q, a, Z0) = (q, ε) indicates that in the state q on
seeing a, the current top of symbol Z0 is deleted
form the stack.
3. (q, a, Z0) = (q1, aZ0) indicates that in the state q
on seeing a, a is pushed on to stack and the
state is changed to q1.
21 November 2017
Sampath Kumar S, AP/CSE, SECE
9

10. Representation of PDA
PDA can be represented using
1. Transition Diagram
2. Transition Table
3. Instantaneous Description (ID)
21 November 2017
Sampath Kumar S, AP/CSE, SECE
10

11. Transition Diagram:
 The following diagram shows a transition in a PDA from
a state q1 to state q2, labeled as a,b → c
 This means at state q1, if we encounter an input
string ‘a’ and top symbol of the stack is ‘b’, then we
pop ‘b’, push ‘c’ on top of the stack and move to
state q2.
21 November 2017
Sampath Kumar S, AP/CSE, SECE
11

12. Instantaneous Description of PDA
 At any given instance, the configuration of PDA is
expressed by the state of finite control, contents of
the stack and the input.
 The instantaneous description (ID) of a PDA is
represented by a triplet W where
 q is the state
 w is unconsumed input
 s is the stack contents, where leftmost symbol
corresponds to the top of the stack (TOS) and right
most is the element beneath it in stack.
21 November 2017
Sampath Kumar S, AP/CSE, SECE
12

13. Language Acceptance by PDA:
A language can be accepted by PDA using 2
approaches:
1. Acceptance by final state: The PDA accepts its
input by consuming it and finally it enters in the
final state.
2. Acceptance by empty stack: on reading the
input string from the initial configuration for some
PDA, the stack of PDA becomes empty.
21 November 2017
Sampath Kumar S, AP/CSE, SECE
13

14. 21 November 2017
Sampath Kumar S, AP/CSE, SECE
14

15. நன்றி
21 November 2017
Sampath Kumar S, AP/CSE, SECE
15