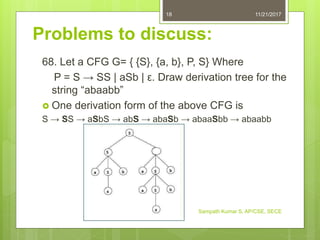
This document discusses derivations and languages in context-free grammars. It covers recursive inference versus derivation to determine if a string belongs to a language. It also discusses leftmost and rightmost derivations, derivation trees, sentential forms, and left and right recursive grammars. Several example problems are provided to demonstrate derivations, parse trees, and generating strings from given grammars.




![Problems to discuss:
61. For the language L = {wcwR | w (0+1)*} check
whether the string 01c10 belongs to the language
L or not.
Solution:
Step 1: For the language L, the productions are
S → 0S0 | 1S1 | C
Step 2: Derivation
S → 0S0 [∵ S → 0S0]
→ 01E10 [∵ S → 1S1]
→ 01c10 [∵ S → c]
11/21/2017
Sampath Kumar S, AP/CSE, SECE
5](https://image.slidesharecdn.com/2-171121154539/85/2-4-derivations-and-languages-5-320.jpg)