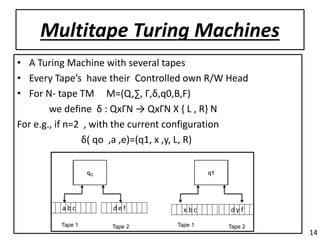
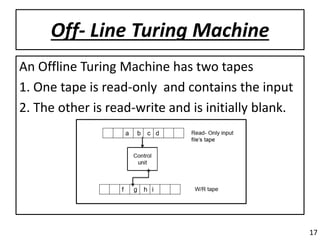
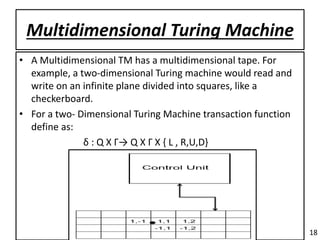
This presentation discusses Turing machines. It introduces Turing machines as a simple mathematical model of a computer that models computing capability. A Turing machine is represented as a 7-tuple that includes the finite set of states, input symbols, tape symbols, transition function, start state, blank symbol, and accepting states. The presentation covers various topics such as the Turing machine model, uses of Turing machines as language recognizers and generators, transition functions, instantaneous descriptions, variations of Turing machines, recursive and recursively enumerable languages, universal Turing machines, and properties of Turing machines.

1. A Presentation
On
“Turing Machine”
Guided By :
Mr. Mohit Saxena
HoD CSE Department
Presented By :
Aniket Kandara
(17EAXCS004)
Session 2019-20
Apex Institute of Engineering and Technology, Jaipur
Department of Computer Science and Technology

2. CONTENT
S.No. TOPIC SLIDE NO.
1. Introduction of Turing Machine 4
2. What is Turing Machine ? 5
3. Representation of Turing Machine 6
4. Turing Machine Model 7
5. Uses of Turing Machine 8
6. Turing Machine as Language Acceptor 9
7. Turing Machine as Transducer 10
8. Transition Function 11
9. ID of Turing Machine 12
10. Techniques of TM Construction 13
11. Variations of Turing Machine 14
12. Recursive and Recursively Enumerable Language 22
TO BE CONTINUED...

3. 13. Universal Language and Turing Machine 23
14. Properties of Turing Machine 24

4. INTRODUCTION OF TURING
MACHINES
• Introduced by Alan Turing in
1936.
• A simple mathematical model of
a computer.
• Models the computing capability
of a computer.
4

5. WHAT IS TURING MACHINE ?
• A Turing machine (TM) is a finite-state
machine with an infinite tape and a tape head
that can read or write one tape cell and move
left or right.
• It normally accepts the input string, or
completes its computation, by entering a final
or accepting state.
• Tape is use for input and working storage.
5

6. Representation of Turing Machine
Turing Machine is represented by
M=(Q,∑, Γ,δ,q0,B,F)
Where
Q is the finite set of states
∑ a set of Γ not including B, is the set of input symbols,
Γ is the finite set of allowable tape symbols,
δ is the next move function, a mapping from Q × Γ to Q × Γ
×{L,R}
Q0 in Q is the start state,
B a symbol of Γ is the blank,
F is the set of final states.
6

7. TURING MACHINE MODEL
7

8. USES OF TURING MACHINE
• Turing machine as a language recognizer.
• Turing machine as a language generator.
• Turing machine as a language evaluator.
• Turing machine as a language decider.
8

9. TURING MACHINE AS LANGUAGE
ACCEPTORS
• A Turing machine halts when it no longer
has available moves.
• If it halts in a final state, it accepts its
input, otherwise it rejects its input.
9

10. TRANSITION FUNCTION
One move (denoted by |---) in a TM does the
following:
δ(q , X) = (p ,Y ,R/L)
Where
• q is the current state.
• X is the current tape symbol pointed by tape
head.
• State changes from q to p.
10

11. INSTANTANEOUS DESCRIPTION (ID)
OF A TURING MACHINE ™
Instantaneous Description or ID :
X1 X2…Xi-1 q Xi Xi+1 … Xn
Means:
q is the current state Tape head is pointing to
Xi X1X2…Xi-1XiXi+1… Xn
are the current tape symbols
• δ (q , Xi ) = (p ,Y , R ) is same as:
X1 X2…Xi-1 q Xi Xi+1 …Xn |---- X1 X2…Xi-1 Y p Xi+1…Xn
• δ (q Xi) = (p, Y, L) is same as:
X1 X2…Xi-1 q Xi Xi+1 …Xn |---- X1 X2…pXi-1Y Xi+1 …Xn
11

12. TECHNIQUES FOR TM
CONSTRUCTION
• Storage in the finite control
• Using multiple tracks
• Using Check off symbols
• Shifting over
• Implementing Subroutine
12

13. VARIATIONS OF TURING MACHINES
• Multitape Turing Machines
• Non deterministic Turing machines
• Multihead Turing Machines
• Off-line Turing machines
• Multidimensional Turing machines
13

14. Multitape Turing Machines
• A Turing Machine with several tapes
• Every Tape’s have their Controlled own R/W Head
• For N- tape TM M=(Q,∑, Γ,δ,q0,B,F)
we define δ : QxΓN → QxΓN X { L , R} N
For e.g., if n=2 , with the current configuration
δ( qo ,a ,e)=(q1, x ,y, L, R)
14

15. Non Deterministic Turing Machines
• It is similar to DTM except that for any
input symbol and current state it has a
number of choices
• A string is accepted by a NDTM if there is
a sequence of moves that leads to a final
state
15

16. Multihead Turing Machine
• Multihead TM has a number of heads instead
of one.
• Each head independently read/ write symbols
and move left / right or keep stationery.
16

17. Off- Line Turing Machine
An Offline Turing Machine has two tapes
1. One tape is read-only and contains the input
2. The other is read-write and is initially blank.
17

18. Multidimensional Turing Machine
• A Multidimensional TM has a multidimensional tape. For
example, a two-dimensional Turing machine would read and
write on an infinite plane divided into squares, like a
checkerboard.
• For a two- Dimensional Turing Machine transaction function
define as:
δ : Q X Γ→ Q X Γ X { L , R,U,D}
18

19. Turing Machine With Semi- Infinite
Tape
• A Turing machine may have a “semi-infinite tape”,
the nonblank input is at the extreme left end of the
tape.
• Turing machines with semi-infinite tape are
equivalent to Standard Turing machines.
19

20. Turing Machine With Stationary
Head
• Here TM head has one another choice of
movement is stay option , S.
• We define new transaction function,
δ : Q X Γ Q X Γ X { L , R, S}
20

21. RECURSIVE AND RECURSIVELY
ENUMERABLE LANGUAGE
The Turing machine may
1. Halt and accept the input
2. Halt and reject the input, or
3. Never halt /loop.
• Recursively Enumerable Language: There is a TM for
a language which accept every string otherwise not.
• Recursive Language: There is a TM for a language
which halt on every string 21

22. UNIVERSAL LANGUAGE AND
TURING MACHINE
• The universal language Lu is the set of binary
strings that encode a pair (M , w) where w is
accepted by M
• A Universal Turing machine (UTM) is a Turing
machine that can simulate an arbitrary Turing
machine on arbitrary input.
22

23. PROPERTIES OF TURING MACHINES
• A Turing machine can recognize a language iff
it can be generated by a phrase-structure
grammar.
• The Church-Turing Thesis: A function can be
computed by an algorithm iff it can be
computed by a Turing machine.
23