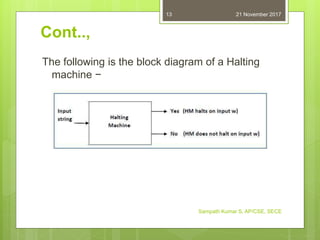
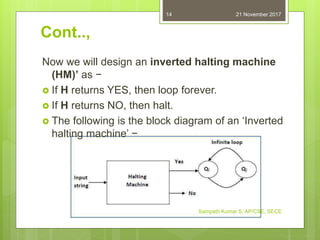
The document discusses the halting problem and decidability of languages. It defines a decidable language as one where a Turing machine can accept or reject every input string and halt. The halting problem asks whether it is possible to determine if an arbitrary Turing machine will halt on a given input. The document proves the halting problem is undecidable by constructing a machine that contradicts itself, showing no algorithm can correctly determine if all Turing machines halt on all inputs.

1. Halting
Problem
-Sampath Kumar S,
AP/CSE, SECE

2. Language Decidability
 A language is called Decidable or Recursive if there
is a Turing machine which accepts and halts on
every input string w.
 Every decidable language is Turing-Acceptable.
21 November 2017
Sampath Kumar S, AP/CSE, SECE
2

3. Decidable Problem
 A Problem is said to be decidable if there exist an
algorithm which can solve the problem in finite
amount of time.
 There are some specific problems that are
algorithmically unsolvable.
21 November 2017
Sampath Kumar S, AP/CSE, SECE
3

4. Decidable Problem
 A decision problem P is decidable if the
language L of all yes instances to Pis decidable.
 For a decidable language, for each input string, the
TM halts either at the accept or the reject state as
depicted in the following diagram −
21 November 2017
Sampath Kumar S, AP/CSE, SECE
4

5. Example 1:
 Find out whether the following problem is decidable or
not −
Is a number ‘m’ prime?
Solution
 Prime numbers = {2, 3, 5, 7, 11, 13, …………..}
 Divide the number ‘m’ by all the numbers between ‘2’
and ‘√m’ starting from ‘2’.
 If any of these numbers produce a remainder zero,
then it goes to the “Rejected state”, otherwise it goes to
the “Accepted state”. So, here the answer could be
made by ‘Yes’ or ‘No’.
 Hence, it is a decidable problem.
21 November 2017
Sampath Kumar S, AP/CSE, SECE
5

6. Example 2:
Given a regular language L and string w, how can
we check if w ∈ L?
Solution
 Take the DFA that accepts L and check if w is
accepted
21 November 2017
Sampath Kumar S, AP/CSE, SECE
6

7. Language:
 If a language L is decidable, then its
complement L' is also decidable.
 If a language is decidable, then there is an
enumerator for it.
21 November 2017
Sampath Kumar S, AP/CSE, SECE
7

8. Undecidable Languages
 For an undecidable language, there is no Turing
Machine which accepts the language and makes a
decision for every input string w (TM can make
decision for some input string though).
 A decision problem P is called “undecidable” if the
language L of all yes instances to P is not
decidable. Undecidable languages are not
recursive languages, but sometimes, they may be
recursively enumerable languages.
21 November 2017
Sampath Kumar S, AP/CSE, SECE
8

9. Example
 The halting problem of Turing machine
 The mortality problem
 The Post correspondence problem, etc.
21 November 2017
Sampath Kumar S, AP/CSE, SECE
9

10. Halting Problem:
 The output of TM can be:
 Halt: The machine will halt state (Accept/
Reject state) after a finite number of states.
 No Halt: The machine will never reach halt state
(Accept/Reject state), no matter how
long it runs.
21 November 2017
Sampath Kumar S, AP/CSE, SECE
10

11. Halting Problem:
 Now the question arises based on these 2
observation: Given an arbitrary TM and arbitrary
input for the machine, then is it possible to
determine whether the machine will ever halt on
given input? This is called halting problem.
 That means we are asking for a procedure which
enable us to solve the halting problem for every
pair(machine & input). The answer is “no”. That is
halting problem is unsolvable.
21 November 2017
Sampath Kumar S, AP/CSE, SECE
11

12. Halting Problem is unsolvable:
 Input − A Turing machine and an input string w.
 Problem − Does the Turing machine finish computing
of the string w in a finite number of steps? The answer
must be either yes or no.
 Proof − At first, we will assume that such a Turing
machine exists to solve this problem and then we will
show it is contradicting itself. We will call this Turing
machine as a Halting machine that produces a ‘yes’ or
‘no’ in a finite amount of time. If the halting machine
finishes in a finite amount of time, the output comes as
‘yes’, otherwise as ‘no’.
21 November 2017
Sampath Kumar S, AP/CSE, SECE
12

13. Cont..,
The following is the block diagram of a Halting
machine −
21 November 2017
Sampath Kumar S, AP/CSE, SECE
13

14. Cont..,
Now we will design an inverted halting machine
(HM)’ as −
 If H returns YES, then loop forever.
 If H returns NO, then halt.
 The following is the block diagram of an ‘Inverted
halting machine’ −
21 November 2017
Sampath Kumar S, AP/CSE, SECE
14

15. Cont..,
 Further, a machine (HM)2 which input itself is
constructed as follows −
If (HM)2 halts on input, loop forever.
Else, halt.
 Here, we have got a contradiction. Hence, the
halting problem is undecidable.
21 November 2017
Sampath Kumar S, AP/CSE, SECE
15

16. 21 November 2017
Sampath Kumar S, AP/CSE, SECE
16

17. நன்றி
21 November 2017
Sampath Kumar S, AP/CSE, SECE
17