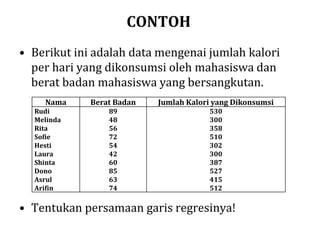
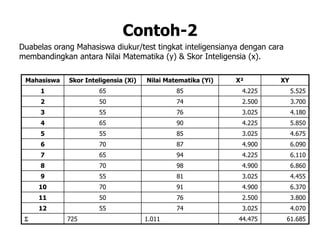
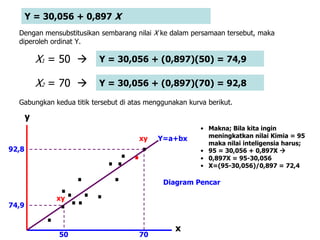
Dokumen tersebut membahas analisis regresi untuk mempelajari hubungan antara variabel bebas dan variabel terikat berdasarkan data-data yang diberikan. Dijelaskan cara menentukan persamaan regresi linier untuk memprediksi nilai variabel terikat berdasarkan nilai variabel bebas. Contoh penerapannya yaitu menentukan hubungan antara skor inteligensi dan nilai mata pelajaran berdasarkan data 12 mahasiswa.

1. Analisis Regresi
Dosen Pengajar:
1) Dr. Ir. Reda Rizal, M.Si. (Lektor Kepala)
2) Ir. Iswahyuni Adil, MM. (Lektor Kepala)
3) Witanti Prihatiningsih, M.Ikom
4) Ir. Drina Intyaswati, M.Si
Red@-Statistika-FISIP-UPN Jakarta 1

2. • Regresi merupakan teknik statistika yang
digunakan untuk mempelajari hubungan
fungsional dari satu atau beberapa peubah bebas
(variabel sebab) terhadap satu peubah tak bebas
(variabel akibat)
• Korelasi merupakan ukuran kekuatan hubungan
dua peubah (tidak harus memiliki hubungan
sebab akibat)

3. Analisis Regresi
(Sir. Francis Galton (1822-1911)
 Untuk mengetahui apakah ada hubungan
antara dua atau lebih variabel. Hubungan
tersebut dinyatakan dalam bentuk rumusan
matematis.
 Persamaan matematis yang memungkinkan kita
dapat meramalkan nilai-nilai variabel tetap
(var. akibat) dari nilai-nilai satu atau lebih
variabel bebas (var. sebab).  Persamaan
Regresi.
 Variabel Tetap (akibat) = Y
 Variabel Bebas (sebab) = X  yang telah diketahui nilainya

4. Regresi Linier
• Persamaan regresi adalah persamaan matematik
yang memungkinkan untuk meramalkan nilai-
nilai suatu variabel tak bebas (y) dari nilai-nilai
satu atau lebih variabel bebas (x).
= a + bxy
• a = intersep/perpotongan garis dengan sumbu tegak
• b = Kemiringan/gradien
• y = nilai ramalan yang dihasilkan garis regresi
• x = nilai pengamatan

5. Persamaan Regresi
Bila diberikan data contoh [(xi, yi); I = 1,2 … n], maka nilai
dugaan kuadrat terkecil bagi parameter dalam garis regresi,
yaitu :
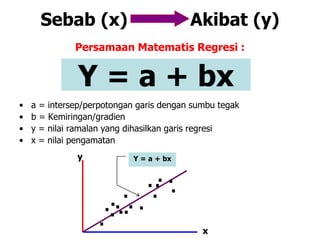
ŷ = a + bx
nilai b dapat diperoleh dari rumus :
Dimana : a = Intersep / perpotongan dengan sumbu tegak
b = Kemiringan
y = Nilai ramalan yang dihasilkan garis regresi

6. CONTOH
• Berikut ini adalah data mengenai jumlah kalori
per hari yang dikonsumsi oleh mahasiswa dan
berat badan mahasiswa yang bersangkutan.
• Tentukan persamaan garis regresinya!
Nama Berat Badan Jumlah Kalori yang Dikonsumsi
Rudi
Melinda
Rita
Sofie
Hesti
Laura
Shinta
Dono
Asrul
Arifin
89
48
56
72
54
42
60
85
63
74
530
300
358
510
302
300
387
527
415
512

7. JAWABAN
• x = jumlah kalori yang dikonsumsi, y = berat badan
S
n
i =1
xi yi - S
n
i =1
yi
( )( )S
n
i =1
xi
x2
i -
( )Si =1
yi
n
S
n
i =1
2b =
y
10 (279.292) - (4141) (643)
10 (180.233) - (4141)2
b =
130.257
874.469
b =
b = 0,149
a = y - b . x
a = 64,3 - (0,149) . (414,1)
jadi persamaan regresinya :
= 2,608 + 0,149 .x
S
10
i =1
S
10
i =1
xi = 4141, yi = 643, xi yi = 279.292
x2
i = 180.233 x = 414,1 y = 64,3

8. Y = a + bx
Sebab (x) Akibat (y)
Persamaan Matematis Regresi :
• a = intersep/perpotongan garis dengan sumbu tegak
• b = Kemiringan/gradien
• y = nilai ramalan yang dihasilkan garis regresi
• x = nilai pengamatan
y
x
Y = a + bx
..
.
.
.
. .
...
.
.
.
.
.
.

9. Contoh-2
Duabelas orang Mahasiswa diukur/test tingkat inteligensianya dengan cara
membandingkan antara Nilai Matematika (y) & Skor Inteligensia (x).
Mahasiswa Skor Inteligensia (Xi) Nilai Matematika (Yi) X² XY
1 65 85 4.225 5.525
2 50 74 2.500 3.700
3 55 76 3.025 4.180
4 65 90 4.225 5.850
5 55 85 3.025 4.675
6 70 87 4.900 6.090
7 65 94 4.225 6.110
8 70 98 4.900 6.860
9 55 81 3.025 4.455
10 70 91 4.900 6.370
11 50 76 2.500 3.800
12 55 74 3.025 4.070
S 725 1.011 44.475 61.685

10. Y = a + bx
• Rata-rata x = 725 / 12 = 60,417
• Rata-rata y = 1.011 / 12 = 84,250
(Sxi)²-nSx²
(Syi)(Sxi)-nSxy
=b
(725)²-(12)(44.475)
(1.011)(725)-(12)(61685)
=b
a = Y - bx
a = 84,25 – (0,897)(60,417) = 30,056
= 0,897
Y = 30,056 + 0,897 X

11. Dengan mensubstitusikan sembarang nilai X ke dalam persamaan tersebut, maka
diperoleh ordinat Y.
X1 = 50  Y = 30,056 + (0,897)(50) = 74,9
Y = 30,056 + 0,897 X
X2 = 70  Y = 30,056 + (0,897)(70) = 92,8
Gabungkan kedua titik tersebut di atas menggunakan kurva berikut.
y
x
.
.
.
.
.
.
xy
...
.
.
.
.
.
.
xy
92,8
74,9
Diagram Pencar
50 70
Y=a+bx
• Makna; Bila kita ingin
meningkatkan nilai Kimia = 95
maka nilai inteligensia harus;
• 95 = 30,056 + 0,897X 
• 0,897X = 95-30,056
• X=(95-30,056)/0,897 = 72,4

12. Homework-1
Suatu penelitian dilakukan oleh seorang pedagang untuk menentukan
hubungan antara biaya pemasangan iklan/bulan dan hasil penjuan/bulan.
Biaya Iklan (X) Hasil Penjualan (Y)
Rp. 40 juta Rp. 385 juta
Rp. 20 juta Rp. 400 juta
Rp. 25 juta Rp. 395 juta
Rp. 20 juta Rp. 365 juta
Rp. 30 juta Rp. 475 juta
Rp. 50 juta Rp. 440 juta
Rp. 40 juta Rp. 490 juta
Rp. 20 juta Rp. 420 juta
Rp. 50 juta Rp. 560 juta
Rp. 40 juta Rp. 525 juta
Rp. 25 juta Rp. 480 juta
Rp. 50 juta Rp. 510 juta
Pertanyaan :
• Buatlah diagram pencar.
• Tentukan persamaan garis regresi
untuk meramal hasil penjualan (y)
berdasarkan biaya iklan (x)
• Buatlah estimasi besarnya
penjualan bila pengeluaran iklan
sebesar Rp. 55 juta.