การพยากรณ์

1. บทที่4 การพยากรณ์(ForecastingForecasting)
การนาเสนอภาพนิ่งนี้ จัดทาขึ้นจากหนังสือ การจัดการการผลิตและการปฏิบัติการ แปลถูกต้องตามลิขสิทธิ์โดย รชฏ ขาบุญและคณะ ผู้จัดทาการนาเสนอภาพนิ่ง มิได้มีเจตนาละเมิดลิขสิทธิ์ แต่จัดทาขึ้นเพื่อ วัตถุประสงค์ทางการศึกษาเท่านั้น

2. เนื้อหา
ความหมายของการพยากรณ์
ช่วงเวลาของการพยากรณ์
ประเภทของการพยากรณ์
ขั้นตอนการพยากรณ์
วิธีการพยากรณ์
การพยากรณ์เชิงคุณภาพ
การพยากรณ์เชิงปริมาณ
วิธีการพยากรณ์โดยใช้รูปแบบอนุกรมเวลา
วิธีการพยากรณ์โดยใช้รูปแบบปัจจัยสาเหตุ
1

3. ความสาคัญของการพยากรณ์ 3
การพยากรณ์มีความสาคัญต่อการดาเนินงานเป็น อย่างมาก ซึ่งความสาคัญของการพยากรณ์มีดังนี้ 1.ทาให้ทราบขนาดความต้องการผลิตภัณฑ์ของ ตลาด 2.ทาให้ธุรกิจสามารถลดความสูญเสียที่จะเกิดขึ้นได้ 3.สามารถนาผลจากการพยากรณ์มาเป็นข้อมูลใน การวางแผนกิจกรรมต่างๆให้มีประสิทธิภาพและ ประสิทธิผลสูงสุด เพื่อสร้างความได้เปรียบทางธุรกิจ

4. กรณีศึกษาบริษัทระดับโลก
4 การพยากรณ์สร้างความได้เปรียบ ทางการแข่งขันให้กับบริษัท Tupperwareบริษัท Tupperware เป็นผู้ผลิตกล่องพลาสติกสาหรับใส่กับข้าว ซึ่งประสบ ความสาเร็จในเวทีระดับโลกด้วยยอดขายกว่า 1.1 ล้านล้านดอลลาร์สหรัฐ การ พยากรณ์ความต้องการของลูกค้าที่ Tupperware ถือได้ว่าเป็นกระบวนการที่สาคัญ และเป็นงานที่ต้องทาอย่างต่อเนื่อง โดยกลุ่มทางานซึ่งประกอบไปด้วยผู้จัดการจาก ฝ่า ยต่างๆจะพยากรณ์โดยใช้ข้อมูลในอดีต เหตุการณ์ปัจ จุบันและเหตุการณ์ที่จะ เกิดขึ้นในอนาคต โดยอาศัยเทคนิคของการพยากรณ์ในรูปแบบต่างๆ เพื่อให้กลุ่ม ทางานสามารถวิเคราะห์ยอดขาย วิเคราะห์การตอบรับผลิตภัณฑ์ใหม่จากลูกค้า รวมทั้งทราบตาแหน่งของแต่ละผลิตภัณฑ์ต่างๆ และนาข้อมูลที่ได้มาตัดสินใจขั้น สุดท้ายเพื่อปรับค่าพยากรณ์ให้เหมาะสมที่สุดและนาค่าดังกล่าวไปวางแผนการ ปฏิบัติการทั่วทั้งองค์การต่อไป

5. OM IN ACTION
5 การพยากรณ์ที่ Disney Worldทีมพยากรณ์ของ Disney World จะต้องทาการประมาณผู้เข้าชมในแต่ละวัน และจะต้องพยากรณ์จานวนลูกค้าในแต่ละสัปดาห์แต่ละเดือนและแต่ละปีรวมทั้งใน อีก5 ปีข้างหน้า สาเหตุที่จะต้องมีการพยากรณ์อย่างมากมายเช่นนี้ก็เนื่องจากว่า ตัวเลขดังกล่าวจะเป็นประโยชน์ต่อการตัดสินใจดาเนินกิจกรรมต่างๆโดยที่ทีม พยากรณ์จะใช้วิธีการในการตัดสินใจทั้งในเชิงคุณภาพและเชิงปริมาณซึ่งทีม ดังกล่าวนี้ได้พยากรณ์จานวนผู้เข้าชมสวนสนุกในปีค.ศ.2000 และสามารถทาให้ค่า ความผิดพลาดจากการพยากรณ์มีค่าเป็นศูนย์ได้ ซึ่ง Disney ได้ทาการเก็บข้อมูล ด้วยการใช้แบบสอบถามจากนักท่องเที่ยวกว่า 1 ล้านคนต่อปี ซึ่งพฤติกรรมของ นักท่องเที่ยวจะสามารถนามาสร้างตัวแบบของการพยากรณ์ที่มีความแม่นยามาก ยิ่งขึ้น นอกจากนั้นทีมงานพยากรณ์ยังต้องติดตามสถานการณ์ต่างๆและแนวโน้มของ เศรษฐกิจทุกภูมิภาคทั่วโลกเพื่อนามาใช้ในการวางแผนต่อไป

6. ความหมายของการพยากรณ์ 2
คือ การทานายเหตุการณ์ในอนาคต อาจนา ข้อมูลในอดีตมาพยากรณ์อนาคตโดยใช้หลัก คณิตศาสตร์ ใช้ดุลยพินิจของผู้พยากรณ์ หรืออาจใช้หลายๆวิธีมารวมกัน เพื่อให้การ พยากรณ์มีความแม่นยามากที่สุด

7. ช่วงเวลาของการพยากรณ์ •เหตุการณ์ไม่เกิน3เดือน เช่น การพยากรณ์การวาง แผนการจัดซื้อ การจัดตารางงาน การพยากรณ์ ยอดขาย และการพยากรณ์การผลิต ระยะสั้น •เหตุการณ์อยู่ในช่วง 3 เดือน ถึง 3 ปี เช่น การวางแผน การผลิต การวางแผนด้านงบประมาณเงินสด และ การวิเคราะห์แผนการดาเนินงานต่างๆ ระยะกลาง •เหตุการณ์ที่มากกว่า 3 ปีขึ้นไป เช่น การวางแผนการ ออกแบบผลิตภัณฑ์ใหม่ ค่าใช้จ่ายในการลงทุน การขาย ทาเลที่ตั้ง และการวิจัยและพัฒนา
ระยะยาว
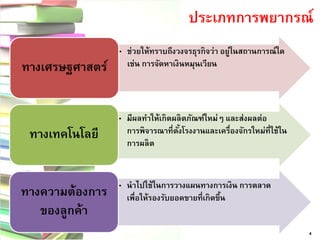
3

8. ประเภทการพยากรณ์
4
•ช่วยให้ทราบถึงวงจรธุรกิจว่า อยู่ในสถานการณ์ใด เช่น การจัดหาเงินหมุนเวียน ทางเศรษฐศาสตร์
•มีผลทาให้เกิดผลิตภัณฑ์ใหม่ๆ และส่งผลต่อ การพิจารณาที่ตั้งโรงงานและเครื่องจักรใหม่ที่ใช้ใน การผลิต
ทางเทคโนโลยี
•นาไปใช้ในการวางแผนทางการเงิน การตลาด เพื่อให้รองรับยอดขายที่เกิดขึ้น
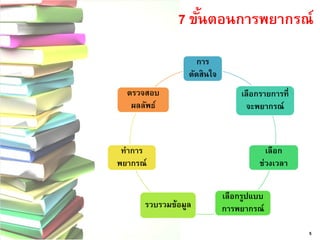
ทางความต้องการ ของลูกค้า

9. 7 ขั้นตอนการพยากรณ์ การ ตัดสินใจ เลือกรายการที่ จะพยากรณ์ เลือก ช่วงเวลา เลือกรูปแบบ การพยากรณ์รวบรวมข้อมูล
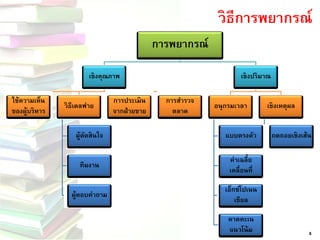
ทาการ พยากรณ์ ตรวจสอบ ผลลัพธ์ 5

10. การพยากรณ์ เชิงคุณภาพ ใช้ความเห็น ของผู้บริหาร วิธีเดลฟาย
ผู้ตัดสินใจ ทีมงาน
ผู้ตอบคาถาม
การประเมิน จากฝ่ายขาย การสารวจ ตลาด เชิงปริมาณ อนุกรมเวลา แบบตรงตัว ค่าเฉลี่ย เคลื่อนที่
เอ็กซ์โปเนน เชียล คาดคะเน แนวโน้ม เชิงเหตุผล
ถดถอยเชิงเส้น
6วิธีการพยากรณ์

11. 7
คือ การพยากรณ์ที่ใช้ลางสังหรณ์ อารมณ์ ความรู้สึก ประสบการณ์ของผู้ตัดสินใจเป็นหลักใน การพยากรณ์
การพยากรณ์เชิงคุณภาพ
มี 4 เทคนิค 1. การใช้ความเห็นของกลุ่มผู้บริหารระดับสูงหรือผู้เชี่ยวชาญ
โดยมากจะผสมรูปแบบทางสถิติเข้าไปเพื่อประมาณความต้องการ หรือแนวโน้มในอนาคต
2. วิธีเดลฟาย วิธีนี้จะใช้บุคคล 3 กลุ่มเข้าร่วมในการพยากรณ์ ได้แก่

12.  ผู้ตัดสินใจ ประกอบด้วยกลุ่มผู้เชี่ยวชาญ 5 - 10 คน ซึ่งจะเป็นคนทาการพยากรณ์ ทีมงาน เป็นผู้ช่วยในด้านการเตรียมงาน เก็บรวบรวม สรุปผลการสารวจ ผู้ตอบคาถาม เป็นกลุ่มเป้าหมายที่ตอบคาถาม 3. การประเมินจากฝ่ายขาย จะให้พนักงานขายประมาณ ยอดขายของตนเอง แล้วนาค่าพยากรณ์แต่ละคนมารวมกัน จะได้ เป็นค่าพยากรณ์ของแต่ละเขตจนถึงระดับประเทศ 4. การสารวจตลาด จะใช้การสอบถามจากลูกค้าถึงแผนการซื้อ ผลิตภัณฑ์ของบริษัทในอนาคต จากนั้นนาผลที่ได้มาใช้ใน การพยากรณ์ความต้องการของลูกค้า
8

13. 9การพยากรณ์เชิงปริมาณ คือ การพยากรณ์ที่ใช้รูปแบบทางคณิตศาสตร์เข้า ช่วย และมักนาข้อมูลในอดีตมาใช้ในการพยากรณ์ แบ่งออกเป็น 2 รูปแบบได้แก่ 1.รูปแบบอนุกรมเวลา ตั้งอยู่บนสมมุติฐานที่ว่าข้อมูลในอดีตจะสามารถใช้พยากรณ์ อนาคตได้ 2.รูปแบบปัจจัยสาเหตุ หรือรูปแบบเชิงเหตุผล เป็นการพยากรณ์ด้วยการวิเคราะห์ปัจจัยต่างๆ ที่จะมี ผลกระทบต่อสิ่งที่พยากรณ์

14. การพยากรณ์โดยใช้รูปแบบ
รูปแบบอนุกรมเวลา
10แบ่งออกเป็น 4 วิธี วิธีการหาค่าแบบตรงตัว
 วิธีการหาค่าเฉลี่ยเคลื่อนที่
 วิธีการปรับเรียบแบบเอ็กซ์โปเนนเชียล
 วิธีการคาดคะเนแนวโน้ม

15. วิธีการหาค่าแบบตรงตัว
“ความต้องการในอนาคต = ความต้องการปัจจุบัน”
เช่น เดือนนี้ขายรองเท้าได้ 100คู่
สามารถพยากรณ์ได้ว่า : เดือนหน้าก็จะขายรองเท้าได้100คู่ด้วย
(ต้นทุนต่า รวดเร็ว แต่คลาดเคลื่อนมาก)
11

16. =
วิธีการหาค่าเฉลี่ยเคลื่อนที่
ค่าเฉลี่ยเคลื่อนที่แบบอย่างง่าย
(Simple moving average) n = จานวนช่วงเวลาในค่าเฉลี่ยเคลื่อนที่ที่ต้องการ เช่น 3, 4 หรือ5เดือน (โจทย์กาหนดให้) 12

17. ค่าเฉลี่ยเคลื่อนที่แบบอย่างง่าย
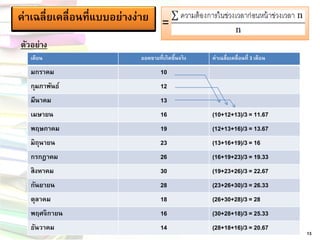
ตัวอย่าง
= 13
เดือน
ยอดขายที่เกิดขึ้นจริง
ค่าเฉลี่ยเคลื่อนที่ 3 เดือน
มกราคม
10
กุมภาพันธ์
12
มีนาคม
13
เมษายน
16
(10+12+13)/3 = 11.67
พฤษภาคม
19
(12+13+16)/3 = 13.67
มิถุนายน
23
(13+16+19)/3 = 16
กรกฎาคม
26
(16+19+23)/3 = 19.33
สิงหาคม
30
(19+23+26)/3 = 22.67
กันยายน
28
(23+26+30)/3 = 26.33
ตุลาคม
18
(26+30+28)/3 = 28
พฤศจิกายน
16
(30+28+18)/3 = 25.33
ธันวาคม
14
(28+18+16)/3 = 20.67

18. วิธีการหาค่าเฉลี่ยเคลื่อนที่
ค่าเฉลี่ยเคลื่อนที่แบบถ่วงน้าหนัก
(Weighted moving average)
n = จานวนช่วงเวลาในค่าเฉลี่ยเคลื่อนที่ที่ต้องการ เช่น 3, 4 หรือ5เดือน (โจทย์กาหนดให้)
= 14

19. ตัวอย่าง
=
15
เดือน
ยอดขายที่เกิดขึ้นจริง
ค่าเฉลี่ยเคลื่อนที่แบบถ่วงน้าหนัก 3 เดือน
มกราคม
10
กุมภาพันธ์
12
มีนาคม
13
เมษายน
16
[(3×13)+(2×12)+(10)]/6 = 12.17
พฤษภาคม
19
[(3×16)+(2×13)+(12)]/6 = 14.33
มิถุนายน
23
[(3×19)+(2×16)+(13)]/6 = 17
กรกฎาคม
26
[(3×23)+(2×19)+(16)]/6 = 20.5
สิงหาคม
30
[(3×26)+(2×23)+(19)]/6 = 23.83
กันยายน
28
[(3×30)+(2×26)+(23)]/6 = 27.5
ตุลาคม
18
[(3×28)+(2×30)+(26)]/6 = 18.33
พฤศจิกายน
16
[(3×18)+(2×28)+(30)]/6 = 23.33
ธันวาคม
14
[(3×16)+(2×18)+(28)]/6 = 18.67
ค่าเฉลี่ยเคลื่อนที่
แบบถ่วงน้าหนัก

20. ค่าถ่วงน้าหนัก
ช่วงเวลา
3
1 เดือนก่อนหน้า
2
2 เดือนก่อนหน้า
1
3 เดือนก่อนหน้า
6
ผลรวมของค่าถ่วง น้าหนัก
ค่าพยากรณ์เดือนนี้
16
การคิดค่าถ่วงน้าหนัก
(3 x ยอดขายของเดือนทีแล้ว) + (2 x ยอดขายของ 2 เดือนก่อนหน้า) + (1 x ยอดขายของ 3 เดือนก่อนหน้า)
ผลรวมของค่าถ่วงน้าหนัก
=

21. Ft= ค่าพยากรณ์ที่ต้องการ
Ft-1 = ค่าพยากรณ์งวดที่แล้ว
α = ค่าคงที่ปรับเรียบ 0<α<1
At-1= ค่าจริงงวดที่แล้ว 17
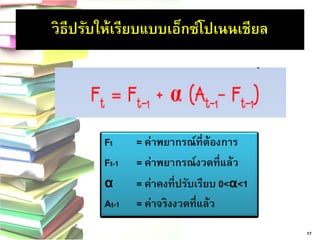
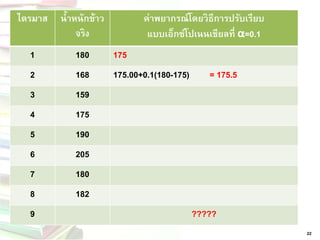
วิธีปรับให้เรียบแบบเอ็กซ์โปเนนเชียล

22. ข้อมูลของช่วงเวลา 8 ไตรมาสของท่าเรือ เกี่ยวกับการขนถ่ายข้าวจากเรือ ผู้บริหารของ ท่าเรือต้องการพยากรณ์ไตรมาสที่9 โดยวิธีการ ปรับเรียบแบบเอ็กซ์โปเนนเชียล
โดยใช้ค่า α = 0.1
คาดว่าจะขนข้าวในไตรมาสแรกได้ 175 ตัน
ตัวอย่าง
21

23. 22
ไตรมาส
น้าหนักข้าว จริง
ค่าพยากรณ์โดยวิธีการปรับเรียบ
แบบเอ็กซ์โปเนนเชียลที่α=0.1
1
180
175
2
168
175.00+0.1(180-175) = 175.5
3
159
4
175
5
190
6
205
7
180
8
182
9
?????

24. 23
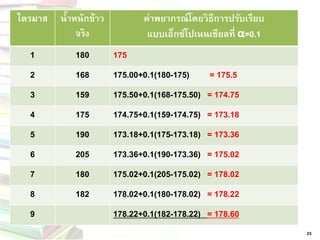
ไตรมาส
น้าหนักข้าว จริง
ค่าพยากรณ์โดยวิธีการปรับเรียบ
แบบเอ็กซ์โปเนนเชียลที่α=0.1
1
180
175
2
168
175.00+0.1(180-175) = 175.5
3
159
175.50+0.1(168-175.50) = 174.75
4
175
174.75+0.1(159-174.75) = 173.18
5
190
173.18+0.1(175-173.18) = 173.36
6
205
173.36+0.1(190-173.36) = 175.02
7
180
175.02+0.1(205-175.02) = 178.02
8
182
178.02+0.1(180-178.02) = 178.22
9
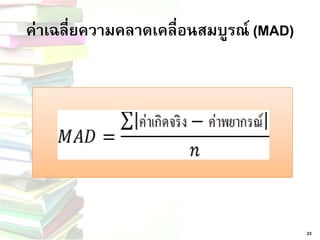
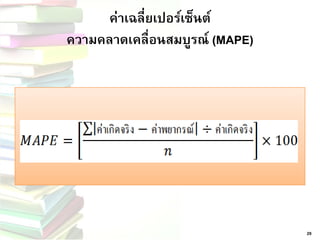
178.22+0.1(182-178.22) = 178.60

25. การคานวณค่าเฉลี่ยความคลาดเคลื่อนมี 3 วิธี •ค่าเฉลี่ยความคลาดเคลื่อนสมบูรณ์ (MAD) •ค่าเฉลี่ยความคลาดเคลื่อนกาลังสอง(MSE)
•ค่าเฉลี่ยเปอร์เซ็นต์ความคลาดเคลื่อนสมบูรณ์ (MAPE)
*** ความคลาดเคลื่อนยิ่งน้อยยิ่งดี
21
การวัดค่าความคาดเคลื่อนของการพยากรณ์

26. ข้อมูลของช่วงเวลา 8 ไตรมาสของท่าเรือ เกี่ยวกับการขนถ่ายข้าวจากเรือ ผู้บริหารของ ท่าเรือต้องการพยากรณ์โดยวิธีการปรับเรียบ แบบเอ็กซ์โปเนนเชียล
โดยใช้ค่า α = 0.1
คาดว่าจะขนข้าวในไตรมาสแรกได้ 175 ตัน
จงหาค่าเฉลี่ยความคลาดเคลื่อนทั้งสามแบบ
ตัวอย่าง
22

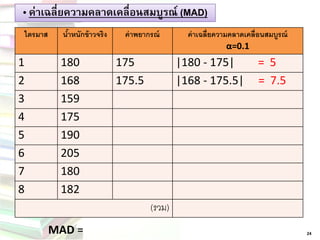
27. ค่าเฉลี่ยความคลาดเคลื่อนสมบูรณ์ (MAD)
/23

28. „ ค่าเฉลี่ยความคลาดเคลื่อนสมบูรณ์ (MAD)
24
ไตรมาส
น้าหนักข้าวจริง
ค่าพยากรณ์
ค่าเฉลี่ยความคลาดเคลื่อนสมบูรณ์ α=0.1
1
180
175
|180 -175| = 5
2
168
175.5
|168 -175.5| = 7.5
3
159
4
175
5
190
6
205
7
180
8
182
(รวม)
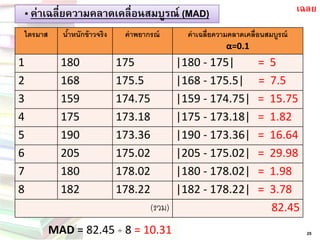
MAD=

29. „ ค่าเฉลี่ยความคลาดเคลื่อนสมบูรณ์ (MAD)
25
ไตรมาส
น้าหนักข้าวจริง
ค่าพยากรณ์
ค่าเฉลี่ยความคลาดเคลื่อนสมบูรณ์ α=0.1
1
180
175
|180 -175| = 5
2
168
175.5
|168 -175.5| = 7.5
3
159
174.75
|159 -174.75| = 15.75
4
175
173.18
|175 -173.18| = 1.82
5
190
173.36
|190 -173.36| = 16.64
6
205
175.02
|205 -175.02| = 29.98
7
180
178.02
|180 -178.02| = 1.98
8
182
178.22
|182 -178.22| = 3.78
(รวม)
82.45
MAD= 82.45 ÷8 = 10.31
เฉลย

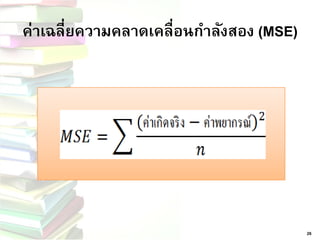
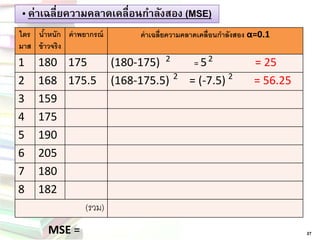
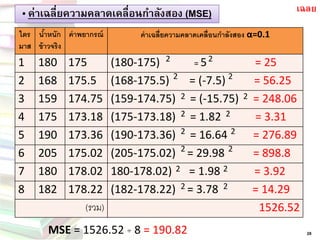
30. ค่าเฉลี่ยความคลาดเคลื่อนกาลังสอง(MSE)
26

31. „ ค่าเฉลี่ยความคลาดเคลื่อนกาลังสอง (MSE)
27
MSE=
ไตร มาส
น้าหนัก ข้าวจริง
ค่าพยากรณ์
ค่าเฉลี่ยความคลาดเคลื่อนกาลังสอง α=0.1
1
180
175
(180-175) = 5 = 25
2
168
175.5
(168-175.5) = (-7.5) = 56.25
3
159
4
175
5
190
6
205
7
180
8
182
(รวม)
2
2
2
2

32. „ ค่าเฉลี่ยความคลาดเคลื่อนกาลังสอง (MSE)
28
ไตร มาส
น้าหนัก ข้าวจริง
ค่าพยากรณ์
ค่าเฉลี่ยความคลาดเคลื่อนกาลังสอง α=0.1
1
180
175
(180-175) = 5 = 25
2
168
175.5
(168-175.5) = (-7.5) = 56.25
3
159
174.75
(159-174.75) = (-15.75) = 248.06
4
175
173.18
(175-173.18) = 1.82 = 3.31
5
190
173.36
(190-173.36) = 16.64 = 276.89
6
205
175.02
(205-175.02) = 29.98 = 898.8
7
180
178.02
180-178.02) = 1.98 = 3.92
8
182
178.22
(182-178.22) = 3.78 = 14.29
(รวม)
1526.52
MSE= 1526.52 ÷8 = 190.82
เฉลย
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2

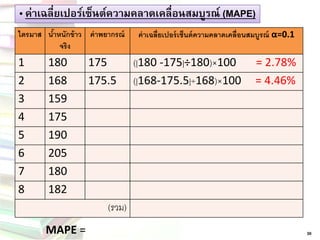
33. ค่าเฉลี่ยเปอร์เซ็นต์ ความคลาดเคลื่อนสมบูรณ์(MAPE)
29

34. „ ค่าเฉลี่ยเปอร์เซ็นต์ความคลาดเคลื่อนสมบูรณ์ (MAPE)
30
MAPE=
ไตรมาส
น้าหนักข้าว จริง
ค่าพยากรณ์
ค่าเฉลี่ยเปอร์เซ็นต์ความคลาดเคลื่อนสมบูรณ์ α=0.1
1
180
175
(|180 -175|÷180)×100 = 2.78%
2
168
175.5
(|168-175.5|÷168)×100 = 4.46%
3
159
4
175
5
190
6
205
7
180
8
182
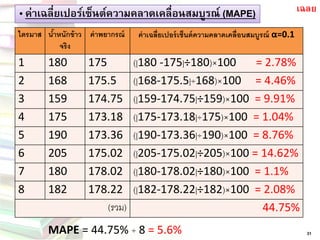
(รวม)

35. „ ค่าเฉลี่ยเปอร์เซ็นต์ความคลาดเคลื่อนสมบูรณ์ (MAPE)
31
ไตรมาส
น้าหนักข้าว จริง
ค่าพยากรณ์
ค่าเฉลี่ยเปอร์เซ็นต์ความคลาดเคลื่อนสมบูรณ์ α=0.1
1
180
175
(|180 -175|÷180)×100 = 2.78%
2
168
175.5
(|168-175.5|÷168)×100 = 4.46%
3
159
174.75
(|159-174.75|÷159)×100 = 9.91%
4
175
173.18
(|175-173.18|÷175)×100 = 1.04%
5
190
173.36
(|190-173.36|÷190)×100 = 8.76%
6
205
175.02
(|205-175.02|÷205)×100 = 14.62%
7
180
178.02
(|180-178.02|÷180)×100 = 1.1%
8
182
178.22
(|182-178.22|÷182)×100 = 2.08%
(รวม)
44.75%
MAPE= 44.75% ÷8 = 5.6%
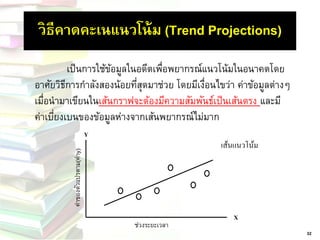
เฉลย

36. วิธีคาดคะเนแนวโน้ม (Trend Projections)
เป็นการใช้ข้อมูลในอดีตเพื่อพยากรณ์แนวโน้มในอนาคตโดย อาศัยวิธีการกาลังสองน้อยที่สุดมาช่วย โดยมีเงื่อนไขว่า ค่าข้อมูลต่างๆ เมื่อนามาเขียนในเส้นกราฟจะต้องมีความสัมพันธ์เป็นเส้นตรง และมี ค่าเบี่ยงเบนของข้อมูลห่างจากเส้นพยากรณ์ไม่มาก
Y
X
เส้นแนวโน้ม
32
ช่วงระยะเวลา
ค่าของตัวแปรตาม(ค่าy)

37. Yˆ  a  bx
วิธีคาดคะเนแนวโน้ม
= ค่าพยากรณ์ตัวแปรตาม
= ค่าคงที่ที่ตัดแกน y
= ค่าความชันของเส้นตรง
แนวโน้ม
= ช่วงระยะเวลา
= ค่าผลรวม
= ค่าเฉลี่ยของเวลา
= ค่าเฉลี่ยของตัวแปรตาม
= ช่วงระยะเวลา
2 2 x nx
xy nxy
b
 
 

a  y  bx
Yˆ
a
b
x

x
y
n
33

38. ข้อมูลความต้องการพลังงานไฟฟ้าของ การไฟฟ้าฝ่ายผลิตระหว่างปี ค.ศ. 1999-2005 แสดงในตารางข้างล่าง จง พยากรณ์ความต้องการพลังงานไฟฟ้า ของปี ค.ศ. 2006 โดยใช้วิธีการคาดคะเนแนวโน้ม
37
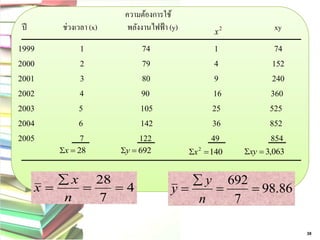
ตัวอย่าง

39. ความต้องการใช้
ปี ช่วงเวลา (x) พลังงานไฟฟ้า (y) xy 2 x
1999 1 74 1 74
2000 2 79 4 152
2001 3 80 9 240
2002 4 90 16 360
2003 5 105 25 525
2004 6 142 36 852
2005 7 122 49 854
4
7
28
 


n
x
x 98.86
7
692
 


n
y
y
38
140 2 x  28 y  692 x  xy  3,063

40. หาค่าคงที่ a , b
2 2 x nx
xy nxy
b
 
 

a  y bx
ดังนั้น สมการแนวโน้มวิธีการกาลังสองน้อยที่สุดจะได้
39
10.54
28
295
140 (7)(4)
3,063 (7)(4)(98.86)
2  



 98.8610.54(4)  56.70
Yˆ  56.7010.54x

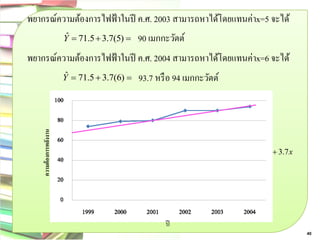
41. พยากรณ์ความต้องการไฟฟ้าในปี ค.ศ. 2003 สามารถหาได้โดยแทนค่าx=5 จะได้
Yˆ  71.53.7(5)  90 เมกกะวัตต์
เส้นพยากรณ์แนวโน้ม Yˆ  71.5  3.7x
พยากรณ์ความต้องการไฟฟ้าในปี ค.ศ. 2004 สามารถหาได้โดยแทนค่าx=6 จะได้
Yˆ  71.5  3.7(6)  93.7 หรือ 94 เมกกะวัตต์
ความต้องการพลังงาน
ปี
40

42. การพยากรณ์โดยใช้ รูปแบบปัจจัยสาเหตุ
38
เป็นการพยากรณ์ที่จะพิจารณาตัว แปรหลายๆตัวที่มีผลกระทบต่อค่า พยากรณ์ เช่น การพยากรณ์ยอดขาย อาจจะขึ้นอยู่กับตัวแปร งบโฆษณา การ ตั้งราคา อัตราการว่างงาน เป็นต้น

43. การถดถอยเชิงเส้น (Linear regression analysis)
แนวคิดคล้ายกับวิธีการคาดคะเนแนวโน้ม เพียงแต่ตัวแปรอิสระจะไม่ใช่
เรื่องของช่วงเวลาเพียงอย่างเดียว จะเป็นตัวแปรอิสระอื่นๆ ที่ส่งผลต่อ
ตัวแปรตาม แต่ข้อมูลต้องสัมพันธ์กันแบบเส้นตรง ดังนัน้สมการ
พยากรณ์ยังคงมีรูปแบบเหมือนเดิมคือ
Yˆ  a  bx
39

44. Yˆ  a  bx
วิธีถดถอยเชิงเส้น
= ค่าพยากรณ์ตัวแปรตาม
= ค่าคงที่ที่ตัดแกน y
= ค่าความชันของเส้นถดถอย
= ค่าตัวแปรอิสระ
(ไม่จาเป็นต้องเวลา)
= ค่าผลรวม
= ค่าเฉลี่ยของตัวแปรอิสระ
= ค่าเฉลี่ยของตัวแปรตาม
= จานวนของข้อมูล
2 2 x nx
xy nxy
b
 
 

a  y  bx
Yˆ
a
b
x

x
y
n
40

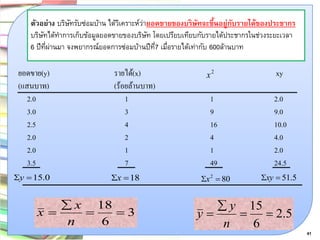
45. ตัวอย่าง บริษัทรับซ่อมบ้าน ได้วิเคราะห์ว่ายอดขายของบริษัทจะขึ้นอยู่กับรายได้ของประชากร
บริษัทได้ทาการเก็บข้อมูลยอดขายของบริษัท โดยเปรียบเทียบกับรายได้ประชากรในช่วงระยะเวลา
6 ปีที่ผ่านมา จงพยากรณ์ยอดการซ่อมบ้านปีที่7 เมื่อรายได้เท่ากับ 600ล้านบาท
ยอดขาย(y) รายได้(x) xy
(แสนบาท) (ร้อยล้านบาท)
2.0 1 1 2.0
3.0 3 9 9.0
2.5 4 16 10.0
2.0 2 4 4.0
2.0 1 1 2.0
3.5 7 49 24.5
2 x
y 15.0 x 18 80 2 x  xy  51.5
3
6
18
 


n
x
x 2.5
6
15
 


n
y
y
41

46. หาค่าคงที่ a , b
2 2 x nx
xy nxy
b
 
 

2 80 (6)(3)
51.5 (6)(3)(2.5)



a  y bx  2.50.25(3) 1.75
ดังนั้น สมการแนวโน้มวิธีการกาลังสองน้อยที่สุดจะได้ Yˆ 1.750.25x
 0.25
42

47. พยากรณ์ยอดการซ่อมบ้านในปีที่ 7
เมื่อรายได้เท่ากับ 600ล้านบาท
จาก
แสนบาท
บาท
Yˆ 1.750.25x
Yˆ 1.75 0.25(6)
Yˆ  3.25
Yˆ  325,000
43
ยอดการซ่อมบ้านในปีที่7 เท่ากับ 325,000บาท