พยากรณ์

1. บทที่ 2 การพยากรณ์ Forecasting

2. การพยากรณ์ คือ อะไร
เป็นกระบวนการคาดการณ์เหตุการณ์ใน อนาคต
เกี่ยวข้องกับการตัดสินใจทางธุรกิจในเรื่อง
การผลิต Production
สินค้าคงคลัง Inventory
ทรัพยากรมนุษย์ Personnel
??

3. การพยากรณ์ระยะสั้น Short-Term Forecasting
โดยทั่วไปไม่เกิน 3 เดือน
เช่น การวางแผนการจัดซื้อ, การจัดตารางการทางาน
การพยากรณ์ระยะกลาง Medium-Term Forecasting
3 เดือน ถึง 3 ปี
เช่น การวางแผนการขาย การผลิต, การจัดทางบประมาณ
การพยากรณ์ระยะยาว Long-Term Forecasting
3 ปีขึ้นไป
เช่น การออกผลิตภัณฑ์ใหม่ การวิจัยพัฒนา การขยายทาเลที่ตั้ง
ระยะเวลาของการพยากรณ์

4. ขั้นตอนการพยากรณ์
การตัดสินใจใช้การพยากรณ์
เลือกรายการการพยากรณ์
ตัดสินใจเวลาที่ใช้ในการพยากรณ์
เลือกรูปแบบการพยากรณ์
รวบรวมข้อมูลที่จาเป็นต่อการทาการพยากรณ์
ทาการพยากรณ์
สร้างความเที่ยงตรงและปฏิบัติการวิเคราะห์ผลลัพธ์

5. ประเภทของการพยากรณ์
1. การพยากรณ์เชิงคุณภาพ
•การพยากรณ์จากรายงานของพนักงานขาย
•การพยากรณ์จากความเห็นของฝ่ายบริหาร
• การสารวจตลาด
• วิธีเดลฟาย

6. ประเภทของการพยากรณ์
โมเดลอนุกรมเวลา Time-series models
โมเดลเหตุผล Associative models, Causal models
2. การพยากรณ์เชิงปริมาณ

7. รูปแบบการพยากรณ์แบบอนุกรมเวลา
 รูปแบบการพยากรณ์ระดับ
 รูปแบบแนวโน้ม
 รูปแบบวัฏจักร
 รูปแบบฤดูกาล

8. © 2006 Prentice Hall, Inc.
4 – 8
เป็นการนาข้อมูลในอดีตมาใช้ในการ พยากรณ์ ลักษณะของข้อมูลขึ้นลงไม่ สม่าเสมอ ทาให้ไม่สามารถคาดการณ์ได้ ขึ้นอยู่กับปัจจัยในช่วงเวลานั้นๆ
รูปแบบการพยากรณ์ระดับ

9. เป็นอนุกรมเวลาที่พิจารณาถึงการเคลื่อนไหว คงที่ขึ้นหรือลงในเหตุการณ์ที่เกิดขึ้นใน ช่วงเวลาที่ต้องการขยายธุรกิจหรือขอบเขต ผลิตภัณฑ์
รูปแบบแนวโน้ม (Trend)
2
3
4
5
0
1
2
3
4
5
6
2006
2007
2008
2009

10. แสดงถึงการผกผันซึ่งเกิดขึ้นในช่วงเวลาที่มากกว่า 1 ปีถ้าช่วงเวลาหรือระบบของวัฎจักรยาวขึ้นอาจจะมี ผลกระทบกับองค์การ เกิดจากผลกระทบจากปัจจัย ด้านการเมือง เศรษฐกิจ วงจรธุรกิจ
รูปแบบวัฎจักร (Cycles)
0 5 10 15 20

11. สะท้อนความผันแปรของข้อมูล ซึ่งกลับมา เกิดขึ้นเป็นช่วงเวลาหรือฤดูกาลในแต่ละปี รูปแบบนี้อาจเป็นช่วงฤดูกาลที่เป็นเดือน ไตรมาสหรือปี และอาจเป็นฤดูกาลที่เป็น สัปดาห์หรือรายวัน หรือแม้กระทั่วรายชั่วโมง ก็เป็นได้ สาเหตุการเปลี่ยนแปลงเกิดจาก พฤติกรรมของลูกค้า หรืออากาศ
รูปแบบฤดูกาล (Seasonal)

12. เกิดในกรณีที่มีความแปรปรวนของวิกฤติการณ์การเมือง การนัดหยุดงาน การประท้วงหรือเหตุการณ์ไม่อาจ คาดการณ์ได้อื่น ๆ ซึ่งไม่อาจใช้การพยากรณ์อนุกรมเวลา แบบใดได้เหมาะสมเพียงพอผู้บริหารจะใช้แบบสุ่มตัวอย่าง โดยทั่วไปแล้วใช้กับเหตุการณ์ที่ไม่ได้กลับมาเกิดขึ้นใหม่อีก ครั้งหรือเป็นเหตุการณ์เกิดขึ้นชั่วครั้งชั่วคราว
รูปแบบสุ่ม (Random)
M T W T F

13. วิธีการพยากรณ์เชิงปริมาณ โมเดลอนุกรมเวลา
1.1 วิธีการหาค่าแบบตรง Naive approach
1.2 วิธีการหาค่าเฉลี่ยเคลื่อนที่ Moving Averages
1.3 วิธีการหาค่าเฉลี่ยเคลื่อนที่ถ่วงน้าหนัก Weighted moving Averages
1.4 วิธีปรับเรียบเอ็กซ์โพเนลเชียล Exponential smoothing
1.5 การวิเคราะห์ถดถอยเชิงเส้นตรง Linear Regression Analysis

14. 1.1 วิธีการหาค่าแบบตรง (Naive Approach)
ความต้องการของผลิตภัณฑ์ในอนาคตจะเท่ากับ ความต้องการปัจจุบัน เช่น ถ้าเดือน พ.ค.ขายได้ 48 เครื่อง ยอดขายเดือน มิ.ย.ก็สามารถพยากรณ์ได้ว่าจะเท่ากับ 48 เครื่อง

15. January 10
February 12
March 13
April 16
May 19
June 23
July 26
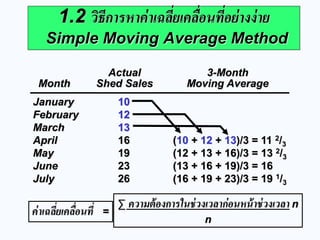
Actual 3-Month Month Shed Sales Moving Average
(12 + 13 + 16)/3 = 13 2/3 (13 + 16 + 19)/3 = 16 (16 + 19 + 23)/3 = 19 1/3
(10 + 12 + 13)/3 = 11 2/3
ค่าเฉลี่ยเคลื่อนที่ =
Σ ความต้องการในช่วงเวลาก่อนหน้าช่วงเวลา n n
1.2 วิธีการหาค่าเฉลี่ยเคลื่อนที่อย่างง่าย Simple Moving Average Method

16. ตัวอย่าง
จากข้อมูลในตารางต่อไปนี้ จงพยากรณ์ยอดขายในเดือนมกราคมปีถัดไป
วิธีทา ค่าเฉลี่ยเคลื่อนที่ 3 เดือน
F13 = Y12 + Y11 + Y10
3
= 14 + 16 + 18
3
= 16

17. ใช้ข้อมูลปัจจุบันมาถ่วงน้าหนัก เพื่อให้การพยากรณ์มี ความถูกต้องมากขึ้น
1.3 วิธีการหาค่าเฉลี่ยเคลื่อนที่ถ่วงน้าหนัก Weighted Moving Average
ค่าเฉลี่ยเคลื่อนที่ถ่วงน้าหนัก
=
Σ [(ค่าถ่วงนน. สาหรับช่วงเวลา n) x (ค่าความต้องการของช่วงเวลา n)] Σ ค่าถ่วงน้าหนักทั้งหมด

18. January 10 February 12 March 13 April 16 May 19 June 23 July 26
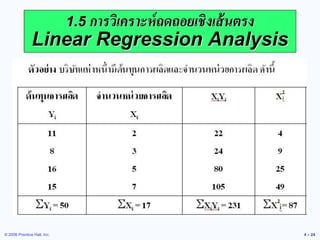
Actual 3-Month Weighted Month Shed Sales Moving Average
(.5 x 16) + (.3 x 13) + (.2 x 12) = 14.30 (.5 x 19) + (.3 x 16) + (.2 x 13) = 16.90 (.5 x 23) + (.3 x 19) + (.2 x 16) = 20.40
Weighted Moving Average
10
12
13
(.5 x 13) + (.3 x 12) + (.2 x 10)= 12.10
Weights Applied Period .50 1 เดือนก่อนหน้า .30 2 เดือนก่อนหน้า .20 3 เดือนก่อนหน้า

19. © 2006 Prentice Hall, Inc.
4 – 19
1.4 วิธีปรับเรียบเอ็กซ์โพเนลเชียล Exponential smoothing
การพยากรณ์โดยใช้การเฉลี่ยเคลื่อนที่วิธีหนึ่ง ซึ่งให้น้าหนัก ข้อมูลที่ผ่านมาแล้วนั้นต่าง ๆ กัน ข้อมูลที่ผ่านมาแล้วนั้นจะ ให้น้าหนักน้อยแล้วเพิ่มขึ้นเรื่อย ๆ จนกระทั่ง ข้อมูลปัจจุบัน จะให้น้าหนักมากที่สุด วิธีนี้ค่าพยากรณ์จะถูกกาหนดโดยค่า พยากรณ์ของงวดที่แล้ว บวกกับส่วนแตกต่างระหว่างข้อมูล จริงของงวดที่แล้วกับค่าพยากรณ์ของงวดที่แล้ว

20. © 2006 Prentice Hall, Inc.
4 – 20
วิธีปรับเรียบเอ็กซ์โพเนลเชียล Exponential smoothing
สูตรในการคานวณ
Ft = Ft-1 +  (Xt-1 – Ft)
เมื่อ Ft ค่าพยากรณ์ความต้องการใหม่
Ft-1 ค่าพยากรณ์ ช่วงที่ผ่านมา
 คือน้าหนักหรือค่าคงที่ปรับเรียบ
Xt-1 ความต้องการที่แท้จริงที่ผ่านมา

21. © 2006 Prentice Hall, Inc.
4 – 21
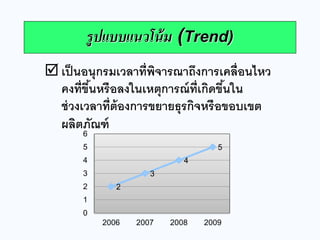
วิธีปรับเรียบเอ็กซ์โพเนลเชียล Exponential smoothing

22. 1.5 การวิเคราะห์ถดถอยเชิงเส้นตรง Linear Regression Analysis
ค่าข้อมูลต่าง ๆ บนเส้นกราฟจะแสดงความสัมพันธ์เป็น เส้นตรง โดยมีค่าเบี่ยงเบนของข้อมูลที่อยู่ห่างจากเส้นกราฟ ไม่มากโดยสามารถหาค่าได้จาก
y = a + bx
y = ค่าพยากรณ์ตัวแปรตาม a = ค่าคงที่ที่ตัดแกน y b = ค่าความชันของเส้นตรงแนวโน้ม x = ค่าตัวแปรอิสระ

23. b =
nSxy - SxSy nSx2 – (Sx)2
y = a + bx
a = y - bx
y = Sy
n
x = Sx
n
1.5 การวิเคราะห์ถดถอยเชิงเส้นตรง Linear Regression Analysis
สูตรในการคานวณ

24. © 2006 Prentice Hall, Inc.
4 – 24
1.5 การวิเคราะห์ถดถอยเชิงเส้นตรง Linear Regression Analysis

25. © 2006 Prentice Hall, Inc.
4 – 25
1.5 การวิเคราะห์ถดถอยเชิงเส้นตรง Linear Regression Analysis
a = y – bx แทนค่า a = 12.5 – 1.254 x 4.25 a = 12.5 – 5.33 a = 7.17

26. © 2006 Prentice Hall, Inc.
4 – 26
1.5 การวิเคราะห์ถดถอยเชิงเส้นตรง Linear Regression Analysis
ถ้าในปีถัดไปจานวนหน่วยผลิตเพิ่มขึ้นเป็น 10 ล้านชิ้น บริษัทแห่งนี้จะมีต้นทุนการผลิตเป็นกี่ล้านบาท
y = a + bx
y = 7.17 + 1.254 x 10
y = 7.17 + 12.54
y = 19.71
ดังนั้น ถ้าในปีถัดไปจานวนหน่วยผลิตเพิ่มขึ้นเป็น 10 ล้าน ชิ้น บริษัทแห่งนี้จะมีต้นทุนการผลิตเป็น 19.71ล้านบาท