การวางแผนกรผลิต

1. บทที่ 4 การวางแผนกาลังการผลิต

2. กาลังการผลิต คือความสามารถสูงสุดของหน่วย
ผลิตที่สามารถจะผลิต รองรับ หรือจัดเก็บได้ใน
หนึ่งช่วงเวลาที่กาหนดซึ่งแยกออกเป็น
2
ความหมายของกาลังการผลิต capacity

3. ความหมายของกาลังการผลิต capacity
3
กาลังการผลิตที่มีประสิทธิผลคือ กาลังผลิตที่องค์การ
คาดหวังจะผลิตสินค้าหรือบริการให้ได้ในระยะเวลาหนึ่ง
ภายใต้เงื่อนไขต่าง ๆ ที่เป็นข้อจากัดของกระบวนการ
กาลังการผลิตตามแผน คือความสามารถสูงสุดตามทฤษฎี
ที่ระบบได้ถูกออกแบบไว้เพื่อให้ได้ผลผลิตที่ต้องการต่อ
หนึ่งหน่วยเวลา

4. ระดับกาลังการผลิต
กาลังการผลิต
สูงสุด กาลังการผลิต
ตามแผน
กาลังการผลิตที่
มีประสิทธิผล
(ระดับที่คาดหวัง)
ระดับกาลังการผลิต
การหยุดพัก ซ่อมแซม
บารุงรักษา
การรองาน รอคน
ประสิทธิภาพของคน
กาลังการผลิต
ตามมาตรฐาน

5. ดัชนีชี้วัดประสิทธิภาพของระบบ
ดัชนีชี้วัดประสิทธิภาพของระบบ
อรรถประโยชน์ = ผลผลิตที่เกิดขึ้นจริง / กาลังการผลิตตามแผน
ประสิทธิภาพ = ผลผลิตที่เกิดขึ้นจริง / กาลังการผลิตที่มี
ประสิทธิผล
5

6. ตัวอย่าง
โรงงานผลิตขนมปังได้ 148,000 ชิ้นโดยร้านได้กาหนดกาลังการผลิตที่
มีประสิทธิผลไว้เท่ากับ 175,000 ชิ้นโดยมีเวลาปฏิบัติงาน 7 วัน ต่อ
สัปดาห์ วันละ 3 กะ ๆ ละ 8 ชั่วโมง สายการผลิต 1,200 ชิ้นต่อชั่วโมง
จงคานวณหา
1. กาลังผลิตตามแผน
2. อรรถประโยชน์
3. ประสิทธิภาพในการผลิต
4. ถ้าประสิทธิภาพในการผลิตมีค่า 75% จงหาอัตราผลผลิตจริง

7. กาลังการผลิต
1. กาลังการผลิตตามแผน = (7 วัน*3กะ*8 ชม.) * (1,200 ชิ้นต่อชม.)
= 201,600 ชิ้นต่อสัปดาห์
2. อรรถประโยชน์ = อัตราผลผลิตที่เกิดขึ้นจริง
กาลังการผลิตตามแผน
= 148,000 = 0.734 or 73.4%
201,600
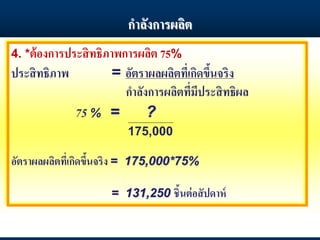
3. ประสิทธิภาพ = อัตราผลผลิตที่เกิดขึ้นจริง
กาลังการผลิตที่มีประสิทธิผล
= 148,000 = 0.846 or 84.6%
175,000

8. กาลังการผลิต
4. *ต้องการประสิทธิภาพการผลิต 75%
ประสิทธิภาพ = อัตราผลผลิตที่เกิดขึ้นจริง
กาลังการผลิตที่มีประสิทธิผล
75 % = ?
175,000
อัตราผลผลิตที่เกิดขึ้นจริง = 175,000*75%
= 131,250 ชิ้นต่อสัปดาห์

9. การวัดกาลังการผลิต
• การวัดกาลังการผลิต สามารถวัดได้ 2 ทางคือ
1) วัดจากผลผลิต 2) วัดจากปัจจัยการผลิต
ระบบการผลิต
Inputs
(ปัจจัยนาเข้า)
Transformation Process
(กระบวนการแปลงสภาพ)
Outputs
(สินค้า/บริการ)
ผลย้อนกลับ (Feed Back)

10. ตัวอย่างการวัดกาลังการผลิต
วัดจากผลผลิต
โรงงานประกอบรถยนต์ จานวนรถยนต์ (คัน/ปี)
โรงงานผลิตเครื่องดื่ม ปริมาตรของเครื่องดื่ม (ลิตร/ปี)
โรงงานอาหารกระป๋ อง น้าหนักของอาหาร (ตัน/ปี)
โรงงานผลิตกระแสไฟฟ้ า กาลังไฟฟ้ า (กิโลวัตต์/ปี)
การเลี้ยงกุ้ง น้าหนักของกุ้ง (ตัน/ปี)
โรงสีข้าว น้าหนักของข้าว (ตัน/ปี)

11. ตัวอย่างการวัดกาลังการผลิต
วัดจากปัจจัยการผลิต
สายการบิน จานวนที่นั่ง
โรงพยาบาล จานวนเตียง
โรงภาพยนตร์ จานวนที่นั่ง
ร้านอาหาร จานวนโต๊ะ
มหาวิทยาลัย จานวนนักศึกษา
ห้างสรรพสินค้า จานวนพื้นที่
อู่ซ่อมรถ จานวนช่างซ่อม

12. การเลือกกาลังการผลิตที่เหมาะสม
1. พยากรณ์ความต้องการลูกค้า ต้องมีความแม่นยา มีการ
ประมาณการความต้องการในอนาคต
2. กาหนดทางเลือกของการเปลี่ยนแปลงกาลังการผลิต ต้อง
คานวณปริมาณการเพิ่ม/ลดที่เหมาะสมให้สอดคล้องกับต้นทุนของการ
ลงทุน
3. เลือกกาลังการผลิตที่เหมาะสมที่สุด กาลังการผลิตที่ทาให้
ต้นทุนเหมาะสม
4. ปรับกาลังการผลิตให้มีความยืดหยุ่น สอดรับกับสถานการณ์
ที่เปลี่ยนแปลง

13. กลยุทธ์การขยายขนาดกาลังการผลิต
Units
Capacity
Time
Demand
การขยายการผลิตนา
Units
Capacity
Time
Demand
การขยายการผลิตตาม
ขยายกาลังการผลิตก่อนที่ความต้องการของลูกค้าจะ
เกิดขึ้น
รักษากาลังการผลิตให้น้อยกว่าความต้องการของ
ลูกค้าเสมอ รอจนความต้องการเพิ่มขึ้นอย่าง
แน่นอนจึงเพิ่มกาลังการผลิต

14. เทคนิคที่ใช้ในการวิเคราะห์และตัดสินใจเลือกกาลังการผลิต
•สถานการณ์ที่แน่นอน
•สถานการณ์ที่มีความ
เสี่ยง
•สถานการณ์ที่ไม่แน่นอน
• เป็นการใช้สาหรับการตัดสินใจ
เพื่อผลลัพธ์ในระยะยาว
• ต้องมีข้อมูลเกี่ยวกับผลได้และ
ต้นทุนของแต่ละทางเลือก
• รู้ความน่าจะเป็นที่จะเกิด
เหตุการณ์ต่างๆ ขึ้น
• เกี่ยวข้องกับการ
กาหนดกาลังการผลิต
สินค้าที่เป็นตัวแปร 2
ตัวภายใต้ข้อจากัดของ
ทรัพยากรที่มีอยู่อย่าง
จากัด
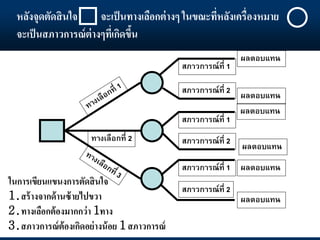
1. ตารางการตัดสินใจ 2. แขนงการตัดสินใจ 3. โปรแกรมเชิงเส้น

15. ตารางการตัดสินใจ
• สถานการณ์ที่แน่นอน
ทางเลือก สูง ปานกลาง ต่า
โรงงานขนาดใหญ่ 20 9 (6)
โรงงานขนาดกลาง 15 11 4
โรงงานขนาดเล็ก 5 5 6
อุปสงค์สูงเลือกสร้างโรงงานขนาดใหญ่
อุปสงค์ปานกลางเลือกสร้างโรงงานขนาดกลาง
อุปสงค์ต่าเลือกสร้างโรงงานขนาดเล็ก
ในความเป็นจริงยากที่จะเกิดสถานการณ์ที่แน่นอนขึ้นในอนาคต

16. ตารางการตัดสินใจ
• สถานการณ์ที่มีความเสี่ยง ต้องพิจารณาผลตอบแทนของแต่ละทางเลือกแล้ว
พิจารณาทางเลือกที่ให้ผลตอบแทนสูงสุด
ทางเลือก สูง ปานกลาง ต่า
โรงงานขนาดใหญ่ 20 9 (6)
โรงงานขนาดกลาง 15 11 4
โรงงานขนาดเล็ก 5 5 6
ความน่าจะเป็น 0.3 0.4 0.3
โรงงานขนาดใหญ่ 0.3(20)+0.4(9)+0.3(-6) = 7.8
โรงงานขนาดกลาง 0.3(15)+0.4(11)+0.3(4) = 10.1
โรงงานขนาดเล็ก 0.3(5)+0.4(5)+0.3(6) = 5.3

17. ตารางการตัดสินใจ
• สถานการณ์ที่ไม่แน่นอน วิธี maximin เลือกค่าตอบแทนสูงสุดจาก
ค่าตอบแทนต่าสุด
ทางเลือก สูง ปานกลาง ต่า ขั้นที่ 1 ขั้นที่ 2
โรงงานขนาดใหญ่ 20 9 (6) (6)
โรงงานขนาดกลาง 15 11 4 4
โรงงานขนาดเล็ก 5 5 6 5 5
เลือกสร้างโรงงานขนาดเล็ก

18. ตารางการตัดสินใจ
• สถานการณ์ที่ไม่แน่นอน วิธี maximax เลือกผลตอบแทนสูงสุดจาก
ค่าตอบแทนสูงสุด
ทางเลือก สูง ปานกลาง ต่า ขั้นที่ 1 ขั้นที่ 2
โรงงานขนาดใหญ่ 20 9 (6) 20 20
โรงงานขนาดกลาง 15 11 4 15
โรงงานขนาดเล็ก 5 5 6 6
เลือกสร้างโรงงานขนาดใหญ่

19. ตารางการตัดสินใจ
• สถานการณ์ที่ไม่แน่นอน วิธี laplace เลือกค่าตอบแทนสูงสุดจาก
ค่าตอบแทนเฉลี่ยของแต่ละทางเลือก
ทางเลือก สูง ปานกลาง ต่า ขั้นที่ 1 ขั้นที่ 2
โรงงานขนาดใหญ่ 20 9 (6) 23/3 =7.65
โรงงานขนาดกลาง 15 11 4 30/3= 10 10
โรงงานขนาดเล็ก 5 5 6 16/3 =5.33
เลือกสร้างโรงงานขนาดกลาง

20. ตารางการตัดสินใจ
• สถานการณ์ที่ไม่แน่นอน วิธี minimax regret เลือกทางเลือกที่มี
ค่าเสียโอกาสต่าสุดจากค่าเสียโอกาสสูงสุด
ทางเลือก สูง ปานกลาง ต่า ขั้นที่ 1 ขั้นที่ 2
ขนาดใหญ่ 20-20 =0 11-9=2 6-(-6) =12 12
ขนาดกลาง 20-15=5 11-11=0 6-4=2 5 5
ขนาดเล็ก 20-5=15 11-5=6 6-6=0 15
เลือกสร้างโรงงานขนาดกลาง

21. แขนงการตัดสินใจ
สี่เหลี่ยม แสดงถึง จุดที่ต้องมีการตัดสินใจ
เส้นตรง แสดงถึง ทางเลือกหรือสภาวการณ์ที่
เกิดขึ้น
วงกลม แสดงถึง จุดที่ระบุว่ามีสภาวการณ์ต่างๆเกิดขึ้น
สัญลักษณ์ที่ใช้
เครื่องมือที่ช่วยตัดสินใจเรื่องการขยายกาลังการผลิตในระยะยาว เช่น ซื้อเครื่องจักรเพิ่ม
ขยายโรงงาน สร้างโรงงานใหม่

22. หลังจุดตัดสินใจ จะเป็นทางเลือกต่างๆ ในขณะที่หลังเครื่องหมาย
จะเป็นสภาวการณ์ต่างๆที่เกิดขึ้น
สภาวการณ์ที่ 1
สภาวการณ์ที่ 1
สภาวการณ์ที่ 1
สภาวการณ์ที่ 2
สภาวการณ์ที่ 2
สภาวการณ์ที่ 2
ทางเลือกที่ 2
ผลตอบแทน
ผลตอบแทน
ผลตอบแทน
ผลตอบแทน
ผลตอบแทน
ผลตอบแทน
ในการเขียนแขนงการตัดสินใจ
1.สร้างจากด้านซ้ายไปขวา
2.ทางเลือกต้องมากกว่า 1ทาง
3.สภาวการณ์ต้องเกิดอย่างน้อย 1 สภาวการณ์

23. โรงงานขนมปังต้องการขยายการผลิตโดยการสร้างโรงงานเพิ่มอีก 1
แห่งคาดว่าจะมีอายุการใช้งาน 5 ปีโรงงานกาลังตัดสินใจว่าจะสร้าง
โรงงานขนาดใหญ่หรือขนาดเล็ก โดยมีรายละเอียดการตัดสินใจดังนี้
ทางเลือก/
อุปสงค์
คชจ.ในการสร้าง
(ล้านบาท)
สูง
(ล้านบาท)
กลาง
(ล้านบาท)
ต่า
(ล้านบาท)
โรงงานขนาด
ใหญ่
2.8 1.3 0.6 - 0.2
โรงงานขนาด
เล็ก
1.5 0.2 0.4 0.5
ความน่าจะเป็น 0.3 0.4 0.3
ตัวอย่างการวิเคราะห์แบบแขนงการตัดสินใจ

24. หลังจุดตัดสินใจ จะเป็นทางเลือกต่างๆ ในขณะที่หลังเครื่องหมาย
จะเป็นสภาวการณ์ต่างๆที่เกิดขึ้น
อุปสงค์สูง P=0.3
อุปสงค์กลาง P=0.4
อุปสงค์ต่า P=0.3
อุปสงค์กลาง P=0.4
อุปสงค์สูง P=0.3
อุปสงค์ต่า P=0.3
5(1.3*0.3) = 1.95 ล้านบาท
5(0.6*0.4) = 1.2 ล้านบาท
5(-0.2*0.3) = - 0.3 ล้านบาท
รวม = 2.85 ล้านบาท
2.85
1.85
5(0.2*0.3) = 0.3 ล้านบาท
5(0.4*0.4) = 0.8 ล้านบาท
5(0.5*0.3) = - 0.75 ล้านบาท
รวม = 1.85 ล้านบาท
ลงทุน
2.80
ลงทุน
1.50

25. ถ้าสร้างโรงงานขนาดใหญ่ จะมีผลตอบแทน
= 2.85 - 2.8 = 0.05 ล้านบาท
ถ้าสร้างโรงงานขนาดเล็ก จะมีผลตอบแทน
= 1.85 – 1.5 = 0.35 ล้านบาท
ดังนั้นจึงควรตัดสินใจสร้างโรงงานขนาดเล็กเพราะมีผลตอบแทนสูง
กว่าสร้างโรงงานขนาดใหญ่
สรุปจากโจทย์ตัวอย่าง

26. โปรแกรมเชิงเส้น (Linear Programming)
ใช้สาหรับแก้ปัญหาการจัดทรัพยากรซึ่งมีอยู่อย่างจากัด โดยสามารถใช้ให้เกิด
ประโยชน์สูงสุด โดยประเมินกาลังการผลิตในระยะสั้นเพื่อใช้กาลังการผลิตที่มี
อยู่ผลิตสินค้าในปริมาณที่จะให้ผลตอบแทนสูงสุด มีขั้นตอนหลัก 2 ขั้นตอน
คือ
1. การสร้างตัวแบบ โดยพิจารณาเงื่อนไขต่างๆ เช่น วัตถุประสงค์ ทางเลือก
ข้อจากัด
2. การหาค่าตอบแทนจากตัวแบบกรณี 2 ตัวแปรจะใช้วิธีกราฟ กรณี
มากกว่า 2 ตัวแปรใช้พีชคณิต

27. ประเภทเครื่องจักร เครื่องจักรตัด เครื่องจักรเย็บ
- ชั่วโมงการทางานที่มีอยู่ 450 280
-ชั่วโมงการผลิตเสื้อเชิ้ต 1 ตัว 1.5 1
-ชั่วโมงการผลิตเสื้อคลุม 1 ตัว 2 0.8
เสื้อเชิ้ตทากาไรได้ = 20 บาท/ตัว
เสื้อคลุมทากาไรได้ = 25 บาท/ตัว
สรุปจากโจทย์ตัวอย่าง

28. 1) กาหนดตัวแปรที่จะต้องตัดสินใจ (สมมติให้เป็น X และ Y)
ให้ X คือ จานวนผลิตเสื้อเชิ้ต
ให้ Y คือ จานวนผลิตเสื้อคลุม
2) ตั้งสมการเป้ าหมายและสมการข้อจากัดตามที่โจทย์กาหนด
สมการผลกาไรสูงสุด = 20 X + 25 Y
ภายใต้เงื่อนไข :
ข้อจากัดด้านเวลาของเครื่องตัด 1.5X+2Y < 450 สมการ 1.5X+2Y = 450
ข้อจากัดด้านเวลาของเครื่องเย็บ 1X+.80Y < 280 สมการ 1X+.80Y = 280
จานวนที่ผลิตจะมีค่าติดลบไม่ได้ X, Y > 0
ขั้นตอนการคานวณ

29. โปรแกรมเชิงเส้น (Linear
Programming)
ขั้นตอนหลัก
1. กำหนดสมกำรวัตถุประสงค์ และสมกำรข้อจำกัด
2. แทนค่ำตัวแปร = 0 จะได้ค่ำตัวแปรอีกตัว ในสมกำรข้อจำกัด
3. สร้ำงกรำฟ สมกำรข้อจำกัด จำกข้อ 2
4. หำค่ำจุดตัดสมกำรข้อจำกัด
5. แทนค่ำตัวแปรจำกจุดตัด ข้อ 4 ในสมกำรวัตถุประสงค์
6. เลือกค่ำตัวแปรที่สอดคล้องวัตถุประสงค์

30. สินค้ำ รำคำ ตัด = 450 เย็บ = 280
เสื้อเชิ้ต X1 20 1.5 1
เสื้อคลุม X2 25 2 0.8
ตัวอย่ำง โรงงำนผลิตเสื้อผ้ำสำเร็จรูป ผลิตเสื้อเชิ้ตและเสื้อคลุม
มีกระบวนกำรตัดและเย็บ ให้จัดสรรกำลังกำรผลิตที่ทำให้กำไรสูงสุด
1สมกำรวัตถุประสงค์ สมกำรข้อจำกัด
20X1 + 25X2 = ? 1.5X1 + 2X2  450 1X1 + 0.8X2  280
โปรแกรมเชิงเส้น (Linear
Programming)

31. ขั้นตอนหลัก
1. กำหนดสมกำรวัตถุประสงค์ และสมกำรข้อจำกัด
2. แทนค่ำตัวแปร = 0 จะได้ค่ำตัวแปรอีกตัว ในสมกำรข้อจำกัด
3. สร้ำงกรำฟ สมกำรข้อจำกัด จำกข้อ 2
4. หำค่ำจุดตัดสมกำรข้อจำกัด
5. แทนค่ำตัวแปรจำกจุดตัด ข้อ 4 ในสมกำรวัตถุประสงค์
6. เลือกค่ำตัวแปรที่สอดคล้องวัตถุประสงค์
โปรแกรมเชิงเส้น (Linear
Programming)

32. สมกำรที่ 1 1.5X1 + 2X2  450 2
1.5(0) + 2(x2) = 450
0 + 2x2 = 450
x2 = 225
2
450

1.5(x1) + 2(0) = 450
1.5x1 + 0 = 450
x1 = 300
5.1
450

สมกำรที่ 2 1X1 + 0.8X2  280
(0,225)  (300,0)
1(0) + 0.8(x2) = 280
0 + 0.8x2 = 280
x2 = 350
8.0
280

1(x1) + 0.8(0) = 280
x1 + 0 = 280
x1 = 280
(0,350)  (280,0)

33. ขั้นตอนหลัก
1. กำหนดสมกำรวัตถุประสงค์ และสมกำรข้อจำกัด
2. แทนค่ำตัวแปร = 0 จะได้ค่ำตัวแปรอีกตัว ในสมกำรข้อจำกัด
3. สร้ำงกรำฟ สมกำรข้อจำกัด จำกข้อ 2
4. หำค่ำจุดตัดสมกำรข้อจำกัด
5. แทนค่ำตัวแปรจำกจุดตัด ข้อ 4 ในสมกำรวัตถุประสงค์
6. เลือกค่ำตัวแปรที่สอดคล้องวัตถุประสงค์
โปรแกรมเชิงเส้น (Linear
Programming)

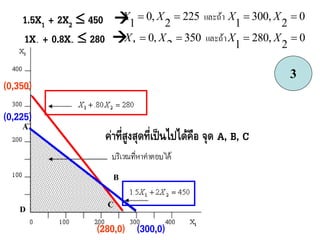
34. 1.5X1 + 2X2  450 
1X1 + 0.8X2  280  0
2
,280
1
350
2
,0
1
0
2
,300
1
225
2
,0
1


XXXX
XXXX
และถ้า
และถ้า
A
B
CD
ค่ำที่สูงสุดที่เป็นไปได้คือ จุด A, B, C
3
(0,350)
(0,225)
(280,0) (300,0)

35. ขั้นตอนหลัก
1. กำหนดสมกำรวัตถุประสงค์ และสมกำรข้อจำกัด
2. แทนค่ำตัวแปร = 0 จะได้ค่ำตัวแปรอีกตัว ในสมกำรข้อจำกัด
3. สร้ำงกรำฟ สมกำรข้อจำกัด จำกข้อ 2
4. หำค่ำจุดตัดสมกำรข้อจำกัด
5. แทนค่ำตัวแปรจำกจุดตัด ข้อ 4 ในสมกำรวัตถุประสงค์
6. เลือกค่ำตัวแปรที่สอดคล้องวัตถุประสงค์
โปรแกรมเชิงเส้น (Linear
Programming)

36. หำค่ำจุด B (หำครน.ให้ตัวเลขหน้ำตัวแปรเท่ำกัน)
หรือ (1) 1.5x1 + 2X2 = 450
(2) 1x1 + 0.8x2 = 280
(2) x 1.5 1.5x1 + 1.2x2 = 420
หรือ (1) 1.5x1 + 2X2 = 450
(2) 1.5x1 + 1.2x2 = 420
(1) – (2) 0.8X2 = 30
X2 = 37.5
หรือ (1) 2x1 + 2X2 = 50
(2) 3x1 + 0.8x2 = 20
(1)x3 6x1 + 6X2 = 150
(2)x2 6x1 + 1.6X2 = 40

37.  
5.37,250
250,280)5.37(8.02
21
112


XXB
XXX
จุดตัดณ
ในแทนค่า
4
หำค่ำจุด B (หำครน.ให้ตัวเลขหน้ำตัวแปรเท่ำกัน)
หรือ (1) 1.5x1 + 2X2 = 450
(2) x 1.5 1.5x1 + 1.2x2 = 420
(1) – (2) 0.8X2 = 30
X2 = 37.5
 
 
   
37.5
601.643
(4)----84040.2332
(3)----9004321
2
2
21
21




X
X
XX
XX
1.5X1 + 2X2  450
1X1 + 0.8X2  280

38. ขั้นตอนหลัก
1. กำหนดสมกำรวัตถุประสงค์ และสมกำรข้อจำกัด
2. แทนค่ำตัวแปร = 0 จะได้ค่ำตัวแปรอีกตัว ในสมกำรข้อจำกัด
3. สร้ำงกรำฟ สมกำรข้อจำกัด จำกข้อ 2
4. หำค่ำจุดตัดสมกำรข้อจำกัด
5. แทนค่ำตัวแปรจำกจุดตัด ข้อ 4 ในสมกำรวัตถุประสงค์
6. เลือกค่ำตัวแปรที่สอดคล้องวัตถุประสงค์
โปรแกรมเชิงเส้น (Linear
Programming)

39. จุด 20X1 25X2 20X1+25X2
A (0,225) 20 x (0) 25 x (225) 5,625
B (250,37.5) 20 x (250) 25 x (37.5) 5,937.50
C (280,0) 20 x (280) 25 x (0) 5,600
D (0,0) 20 x (0) 25 x (0) 0
สมกำร กำไรสูงสุด  20X1 + 25X2
5
6
จะผลิตเสื้อเชิ้ต 250 ตัว เสื้อคลุม 37.5 ตัว ได้กำไรสูงสุด 5,937.50 บำท