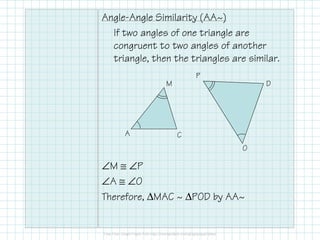
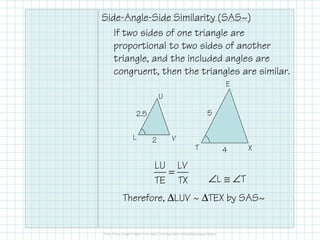
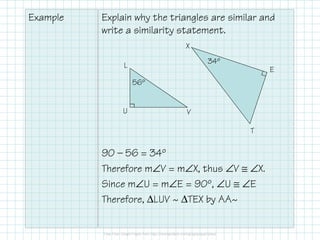
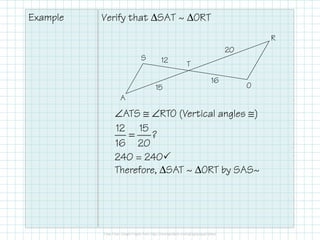
The document outlines the concepts of triangle similarity, including Angle-Angle (AA), Side-Side-Side (SSS), and Side-Angle-Side (SAS) criteria for proving triangles are similar. It provides examples demonstrating how to apply these criteria to establish similarity among triangles. Additionally, it includes specific similarity statements based on given angle and side measurements.

1. 3.8.4 Triangle Similarity
The student is able to (I can):
• Prove certain triangles are similar by using AA~, SSS~,
and SAS~
• Use triangle similarity to solve problems.

2. Angle-Angle Similarity (AA~)
If two angles of one triangle are
congruent to two angles of another
triangle, then the triangles are similar.
∠M ≅ ∠P
∠A ≅ ∠O
Therefore, ∆MAC ~ ∆POD by AA~
M
A C
P
O
D

3. Side-Side-Side Similarity (SSS~)
If the three sides of one triangle are
proportional to the three corresponding
sides of another triangle, then the
triangles are similar.
W H
Y
N
O
T
= =
WH HY WY
NO OT NT
Therefore, ∆WHY ~ ∆NOT by SSS~
1230
18
16
40
24

4. Side-Angle-Side Similarity (SAS~)
If two sides of one triangle are
proportional to two sides of another
triangle, and the included angles are
congruent, then the triangles are similar.
E
T X
U
L V
=
LU LV
TE TX ∠L ≅ ∠T
Therefore, ∆LUV ~ ∆TEX by SAS~
4
5
2
2.5

5. Example Explain why the triangles are similar and
write a similarity statement.
90 — 56 = 34º
Therefore m∠V = m∠X, thus ∠V ≅ ∠X.
Since m∠U = m∠E = 90º, ∠U ≅ ∠E
Therefore, ∆LUV ~ ∆TEX by AA~
56º
34º
L
U V
T
E
X

6. Example Verify that ∆SAT ~ ∆ORT
A
S
T
R
O
12
15
20
16
∠ATS ≅ ∠RTO (Vertical angles ≅)
12 15
?
16 20
=
240 = 240
Therefore, ∆SAT ~ ∆ORT by SAS~