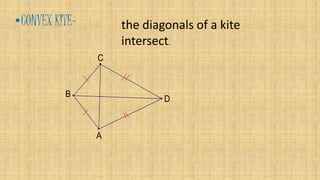
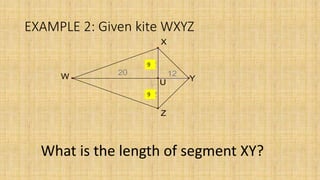
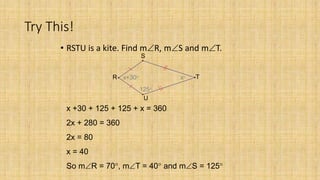
1. A kite is a quadrilateral with two pairs of adjacent congruent sides. Kites were historically used for rituals and are now commonly known as children's toys. 2. A kite has one set of congruent adjacent sides and one set of congruent opposite sides. If a kite's diagonals do not intersect, it is called a dart. 3. The area of a kite is half the product of its diagonals. The diagonals of a kite are perpendicular and bisect the angles between the congruent sides.

1. K I t e

2. Definition
•KITE – is a quadrilateral with two sets of distinct
adjacent congruent sides, but opposite sides are
not congruent.

4. IN ANCIENT TIME
KITE were widely considered to be
useful for ensuring a good harvest or
scaring away evil spirits.

5. IN MODERN TIME
KITE became more widely known as
children's toys and came to be used
primarily as a leisure activity

6. • From the definition, a kite is the only quadrilateral that we
have discussed that could be concave or non convex.
Concave or non convex kite is a kite whose diagonal do not
intersect. If a kite is concave or non convex, it is called
a dart .

7. •CONVEX KITE-
D
C
A
B
the diagonals of a kite
intersect.

8. • The angles between the congruent sides are called vertex
angles . The other angles are called non-vertex angles . If we
draw the diagonal through the vertex angles, we would have
two congruent triangles.
B
A C
D

9. THEOREM 1: The non-vertex angles of a kite are congruent
and the diagonal through the vertex angle is the angle
bisector for both angles.
PROOF:
GIVEN: KITE WITH 𝐾𝐸≅𝑇𝐸 AND 𝐾𝐼≅𝑇𝐼
STATEMENTS REASONS
1. 1.
2. 2.
3. 3.
4. 4.
5. 5.
KITE WITH 𝐾𝐸≅𝑇𝐸 AND 𝐾𝐼≅𝑇𝐼 GIVEN
𝐼𝐸 ≅ 𝐼𝐸 REFLEXIVE PROPERTY
∆𝐾𝐼𝐸 ≅ ∆𝑇𝐼𝐸 SSS CONGRUENCE POSTULATE
∠𝐾 ≅ ∠𝑇 CPCTC
∠𝑇𝐼𝐸 ≅ ∠𝐾𝐼𝐸 AND ∠𝐾𝐸𝐼 ≅ ∠𝑇EI CPCTC
PROVE: ∠𝐾 ≅ ∠𝑇,
∠𝑇𝐼𝐸 ≅ ∠𝐾𝐼𝐸 AND ∠𝐾𝐸𝐼 ≅ ∠𝑇EI

10. THEOREM 2: The diagonals of a kite are perpendicular to
each other.
PROOF:
GIVEN: Kite BCDA
STATEMENTS REASONS
1. 1.
2. 2.
3. 3.
4. 4.
D
C
A
B
Kite BCDA GIVEN
𝐵𝐶≅𝐵𝐴 AND 𝐶𝐷≅𝐴𝐷 Definition of kite
Definition of congruent segments𝐵𝐶 = 𝐵𝐴 AND 𝐶𝐷 = 𝐴𝐷
𝐶𝐴⊥𝐵𝐷 If a line contains two points each of
which is equidistant from the
endpoints of a segment, then the
line is perpendicular bisector of the
segment.
PROVE: 𝑪𝑨⊥𝑩𝑫

11. Theorem 3: The area of a kite is half the product of the
lengths of the diagonals.
w
PROOF:
GIVEN: Kite BCDA
STATEMENTS REASONS
1. 1.
2. 2.
3. 3.
4. 4.
5. 5.
6. 6.
7. 7.
8. 8.
Kite BCDA GIVEN
𝐶𝐴⊥𝐵𝐷
The diagonals of a kite are perpendicular
to each other.
𝑨𝒓𝒆𝒂 𝒐𝒇 𝒌𝒊𝒕𝒆 𝑩𝑪𝑫𝑨
= 𝑨𝒓𝒆𝒂 𝒐𝒇∆𝑩𝑪𝑨 + 𝑨𝒓𝒆𝒂 𝒐𝒇 ∆𝑪𝑫𝑨
Area addition postulate
𝑨𝒓𝒆𝒂 𝒐𝒇∆𝑩𝑪𝑨 =
𝟏
𝟐
(𝑪𝑨)(𝑩𝑾)
𝑨𝒓𝒆𝒂 𝒐𝒇∆𝑪𝑫𝑨 =
𝟏
𝟐
(𝑪𝑨)(𝑫𝑾)
Area formula for triangles
𝐀𝒓𝒆𝒂 𝒐𝒇 𝒌𝒊𝒕𝒆 𝑩𝑪𝑫𝑨
=
𝟏
𝟐
𝑪𝑨 𝑩𝑾 +
𝟏
𝟐
(𝑪𝑨)(𝑫𝑾)
Substitution
𝐀𝒓𝒆𝒂 𝒐𝒇 𝒌𝒊𝒕𝒆 𝑩𝑪𝑫𝑨
=
𝟏
𝟐
𝑪𝑨 𝑩𝑾 + 𝑫𝑾
Associative Property
𝐵𝑊 + 𝐷𝑊 = 𝐵𝐷 Segment Addition Postulate
𝐀𝒓𝒆𝒂 𝒐𝒇 𝒌𝒊𝒕𝒆 𝑩𝑪𝑫𝑨 =
𝟏
𝟐
𝑪𝑨 (𝑩𝑫) Substitution
PROVE:
𝑨𝒓𝒆𝒂 𝒐𝒇 𝒌𝒊𝒕𝒆 𝑩𝑪𝑫𝑨 =
𝟏
𝟐
(𝑪𝑨)(𝑩𝑫)

12. Example 1
•Find the area of the kite WXYZ.
20
12
12
12
U
W
Z
Y
X

13. Example1 Continued
20
12
12
12
U
W
Z
Y
X
We can now use the formula in
finding the area of the kite.
Area of kite WXYZ=
1
2
𝑑1𝑑2
Area of kite WXYZ=
1
2
(𝑋𝑍)(𝑊𝑌)
Area of kite WXYZ=
1
2
(24)(32)
Area of kite WXYZ=384 𝑠𝑞𝑢𝑎𝑟𝑒 𝑢𝑛𝑖𝑡𝑠

14. EXAMPLE 2: Given kite WXYZ
20
12
12
12
U
W
Z
Y
X
9
9
What is the length of segment XY?

15. EXAMPLE 2: Given kite WXYZ
20
12
12
12
U
W
Z
Y
X
9
9
𝑋𝑌2
= 𝑈𝑋2
+ 𝑈𝑌2
𝑋𝑌2
= 92
+ 122
𝑋𝑌2
= 81 + 144
𝑋𝑌2
= 225
XY= 15

16. Example 3
• Find mG and mJ.
60132
J
G
H
K
Since GHJK is a kite G  J
So 2(mG) + 132 + 60 = 360
2(mG) =168
mG = 84 and mJ = 84

17. Try This!
• RSTU is a kite. Find mR, mS and mT.
x
125
x+30
S
U
R T
x +30 + 125 + 125 + x = 360
2x + 280 = 360
2x = 80
x = 40
So mR = 70, mT = 40 and mS = 125

18. QUIZ
• Given kite BCDA and point P be the point of
intersection of the diagonals , consider the given
information below and answer the question that
follows.
1. 𝐶𝐴 = 20𝑚 2.𝐶𝐴 = 14𝑚
𝐵𝐷 = 24𝑚 𝐵𝐶 = 25𝑚
What is the area of kite BCDA? 𝐵𝑃 =?
3. 𝐶𝑃 = 5
𝐶𝐷 = 13
𝐵𝐶 = 74
𝐶𝐴 =?
𝐵𝐷 =?
What is the area of kite BCDA?
D
C
A
B