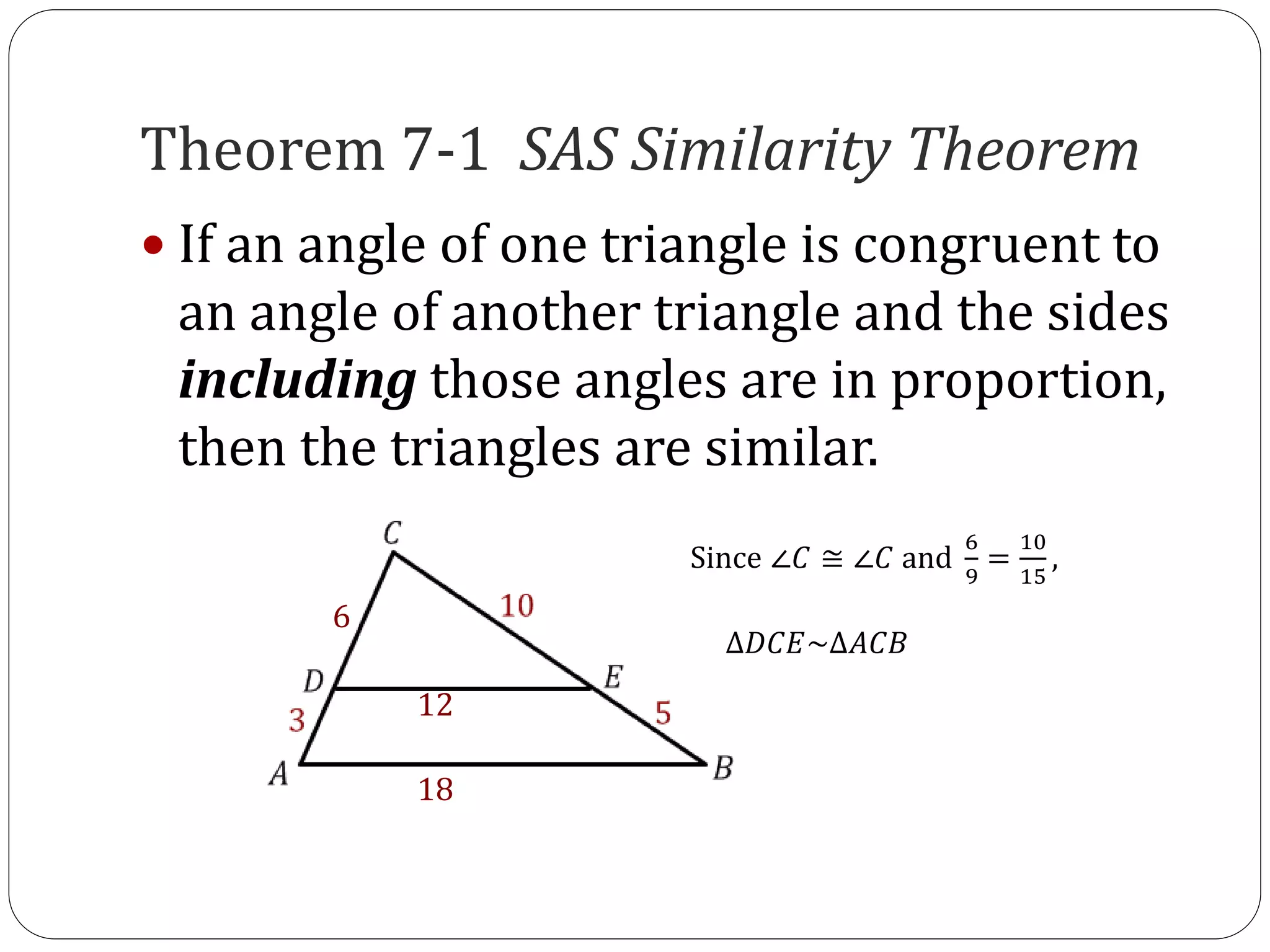
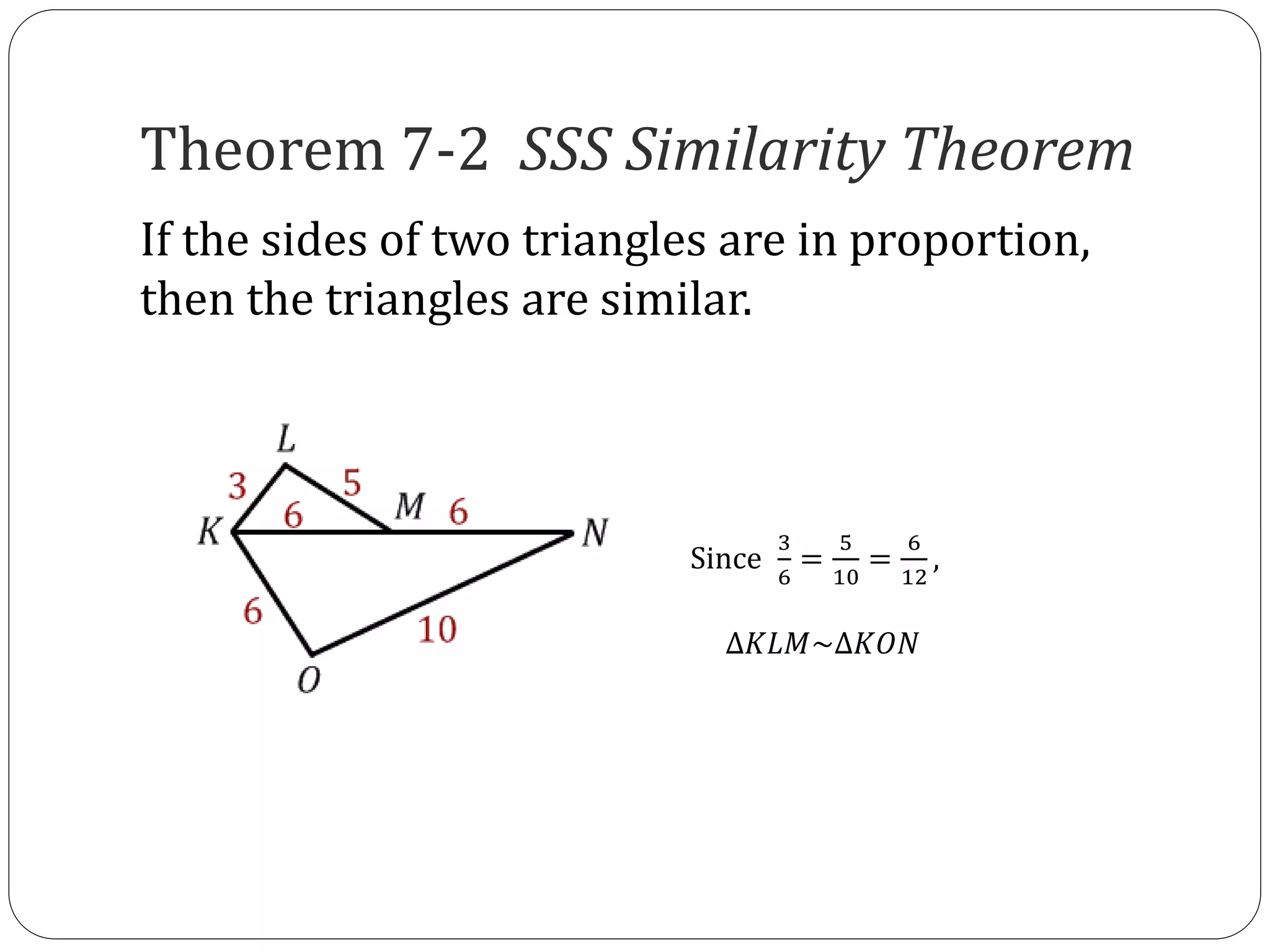
This document discusses three rules for determining if triangles are similar: the AA Similarity Postulate, SAS Similarity Theorem, and SSS Similarity Theorem. It provides examples of applying each rule to determine if triangles are similar, and if so, writing the similarity statement and ratio.

1. 7-4 A Postulate for Similar Triangles
7-5 Theorems for Similar Triangles
Chapter 7 Ratio, Proportion and
Similarity
Objective: I can use the AA Similarity Postulate,
SAS Similarity Theorem and the SSS Similarity
Theorem to prove triangles similar.

2. Postulate 15 AA Similarity
If two angles of one triangle are congruent to two
angles of another triangle, then the triangles are
similar.

3. Theorem 7-1 SAS Similarity Theorem
 If an angle of one triangle is congruent to
an angle of another triangle and the sides
including those angles are in proportion,
then the triangles are similar.
6
12
18
Since ∠𝐶 ≅ ∠𝐶 and
6
9
=
10
15
,
∆𝐷𝐶𝐸~∆𝐴𝐶𝐵

4. Theorem 7-2 SSS Similarity Theorem
If the sides of two triangles are in proportion,
then the triangles are similar.
Since
3
6
=
5
10
=
6
12
,
∆𝐾𝐿𝑀~∆𝐾𝑂𝑁

5. Example 1
 Determine if the triangles are similar. If so, tell
why and write the similarity statement and
similarity ratio.

6. Answers
 Similar : Yes
 Why:SSS Similarity
 Similarity Statement:∆𝑃𝑄𝑅~∆𝑃𝑅𝑆
 Similarity Ratio: 2 to 3

7. Example 2
 Determine if the triangles are similar. If so, tell
why and write the similarity statement and
similarity ratio.

8. Answers
 Similar : Yes
 Why: AA Similarity
 Similarity Statement:∆𝐶𝐵𝐴~∆𝐻𝐺𝐹
 Similarity Ratio: none