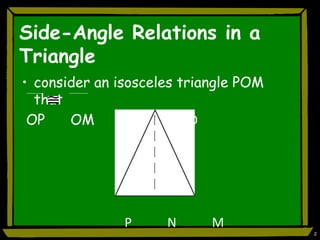
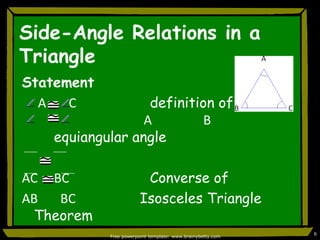
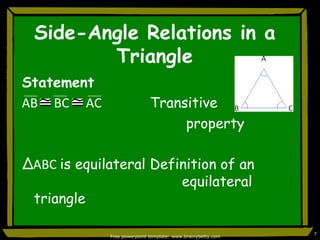
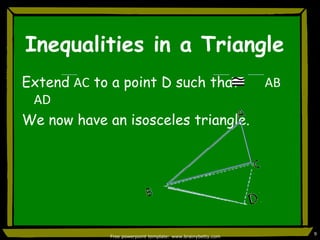
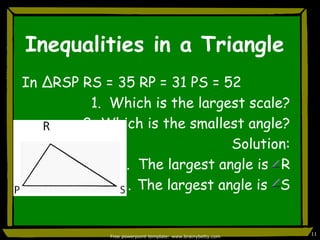
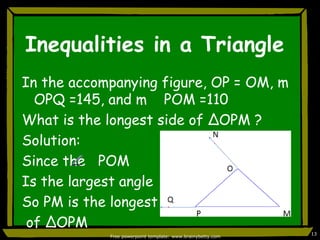
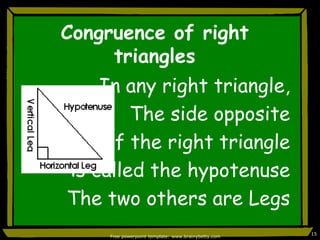
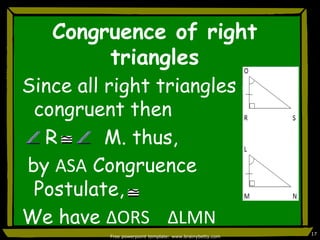
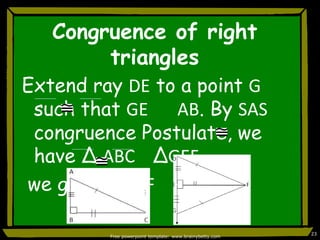
This document discusses triangle congruence and relationships between sides and angles of triangles. It introduces several theorems regarding isosceles, equilateral, and right triangles including: if two sides of a triangle are congruent, the angles opposite them are also congruent; if two angles of a triangle are congruent, the sides opposite them are also congruent; and if corresponding parts of two right triangles are congruent, the triangles are congruent. Examples are provided to demonstrate applying these theorems.

1. USING TRIANGLE CONGRUENCEavery common way of showing that two segments are congruent is by looking them as corresponding angles of congruent triangles

2. 2Side-Angle Relations in a Triangleconsider an isosceles triangle POM thatOPOM OP N M

3. Side-Angle Relations in a TriangleFree powerpoint template: www.brainybetty.com3TheoremIsosceles Triangle Theorem if two sides of a triangle are congruent, then the angles opposite those side are congruent

4. Side-Angle Relations in a TriangleProve that an equilateral triangle ABC is also equiangularStatement ReasonAB BC definition of an equilateral triangle A C Isosceles triangle theoremAB AC Definition of an equilateral triangle B C isosceles triangle theorem A B C Transitive property∆ABC is equiangular. Def. of an equiangular angleFree powerpoint template: www.brainybetty.com4

5. Side-Angle Relations in a TriangleTheoremConverse of Isosceles Triangle Theorem if two angles of a triangle are congruent, then the sides opposite those angles are congruentFree powerpoint template: www.brainybetty.com5

6. Side-Angle Relations in a TriangleStatement Reason A C definition of an AB equiangular angleAC BC Converse ofAB BC Isosceles Triangle TheoremFree powerpoint template: www.brainybetty.com6

7. Side-Angle Relations in a TriangleStatement ReasonAB BC AC Transitive property∆ABC is equilateral Definition of an equilateral triangleFree powerpoint template: www.brainybetty.com7

8. Inequalities in a TriangleIs m C > m B ?Actual measurements shows that the statement is true, but there is a need to reason out why this is so A B CFree powerpoint template: www.brainybetty.com8

9. Inequalities in a TriangleExtendACto a point D such thatABADWe now have an isosceles triangle.Free powerpoint template: www.brainybetty.com9

10. Inequalities in a TriangleTheoremIf two sides of a triangle are not congruent, then the angles opposite these two sides are not congruent, and the larger angle is opposite the longer sideFree powerpoint template: www.brainybetty.com10

11. Inequalities in a TriangleIn ∆RSP RS = 35 RP = 31 PS = 52Which is the largest scale?Which is the smallest angle?Solution:The largest angle is R The largest angle is SFree powerpoint template: www.brainybetty.com11

12. Inequalities in a TriangleTheorem if two angles of a triangle are not congruent, then the sides opposite these two angles are not congruent, and the longer side is opposite the larger angleFree powerpoint template: www.brainybetty.com12

13. Inequalities in a TriangleIn the accompanying figure, OP = OM, m OPQ =145, and m POM =110What is the longest side of ∆OPM ?Solution:Since the POMIs the largest angleSo PM is the longest side of ∆OPMFree powerpoint template: www.brainybetty.com13

14. Congruence of right trianglesFree powerpoint template: www.brainybetty.com14

15. Congruence of right trianglesIn any right triangle,The side oppositeof the right triangle is called the hypotenuseThe two others are LegsFree powerpoint template: www.brainybetty.com15

16. Congruence of right trianglesTheoremLL congruence theorem if the legs of one right triangle are congruent to the legs of another right triangle, then the triangles are congruentFree powerpoint template: www.brainybetty.com16

17. Congruence of right trianglesSince all right triangles are congruent then R M. thus, by ASA Congruence Postulate,We have ∆ORS ∆LMNFree powerpoint template: www.brainybetty.com17

18. Congruence of right trianglesTheoremLA congruence Theorem if a leg and an acute angle of one right triangle are congruent to a leg and an acute angle of another right triangle, then the triangles are congruent.Free powerpoint template: www.brainybetty.com18

19. Congruence of right trianglesSince all right angles are congruent, then T Y. Thus, by SAA congruence postulate, we have∆STU ∆XYZFree powerpoint template: www.brainybetty.com19

20. Congruence of right trianglesTheoremHyACongruence Theorem If an acute angle and the hypotenuse of one right triangle are congruent to a leg and an acute angle of another right triangle, then the triangles are congruent.Free powerpoint template: www.brainybetty.com20

21. HyACongruence TheoremFree powerpoint template: www.brainybetty.com21

22. Congruence of right trianglesTheoremHyLCongruence theoremif a leg and the hypotenuse of one right triangle are congruent to a corresponding leg and the hypotenuse of another right triangle, then the triangles are congruent.Free powerpoint template: www.brainybetty.com22

23. Congruence of right trianglesFree powerpoint template: www.brainybetty.com23Extend ray DE to a point G such that GEAB. By SAS congruence Postulate, we have ∆ ABC ∆GEF. we get AC GF

24. Key ExpressionsFree powerpoint template: www.brainybetty.com24