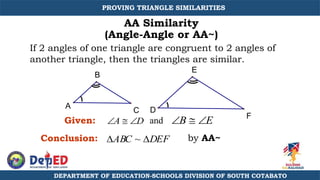
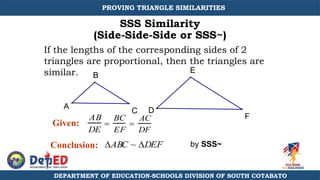
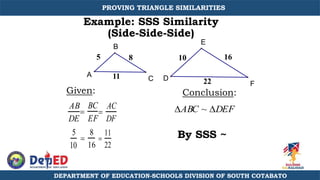
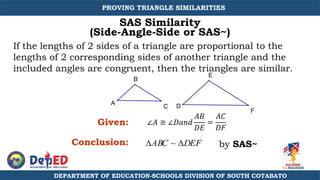
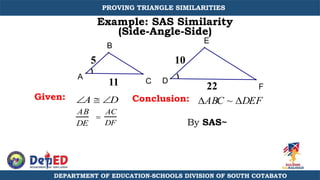
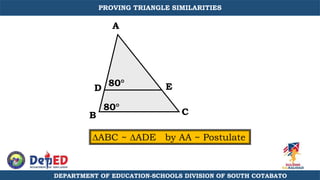
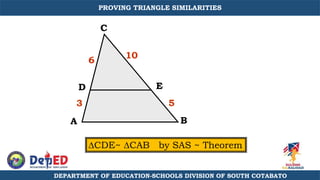
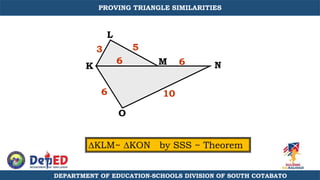
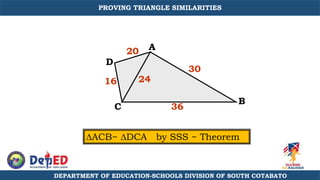
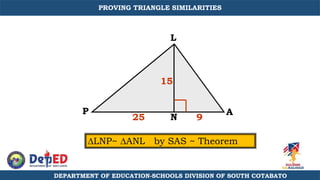
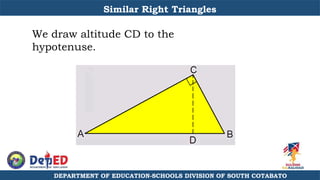
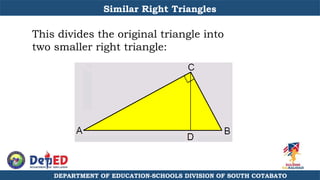
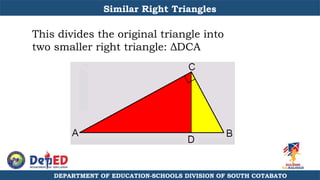
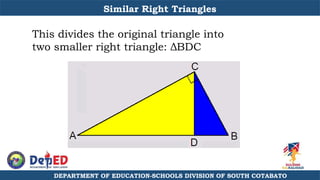
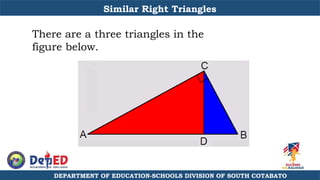
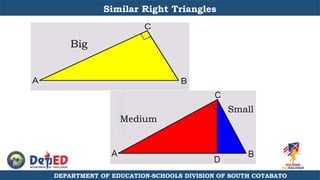
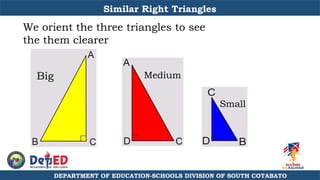
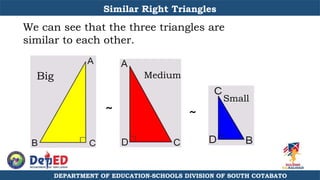
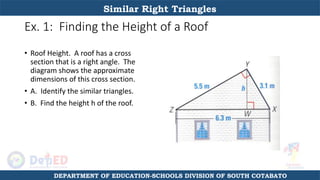
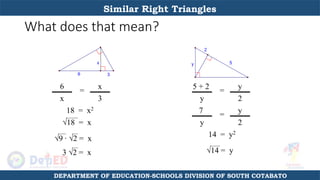
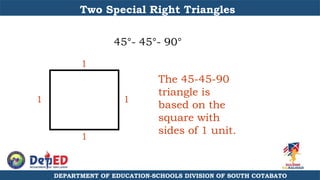
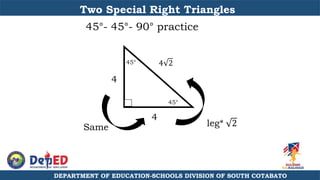
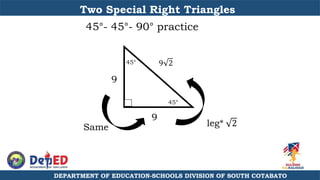
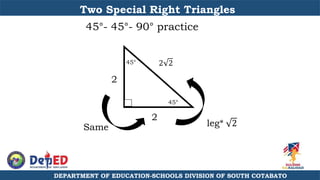
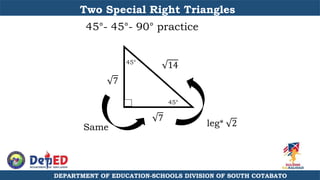
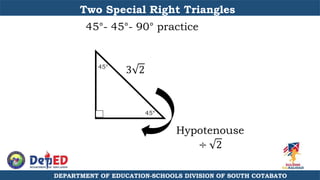
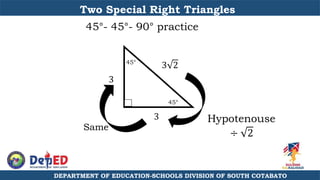
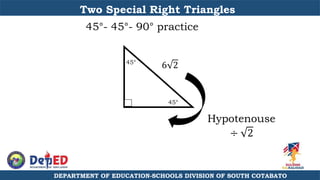
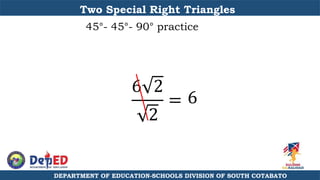
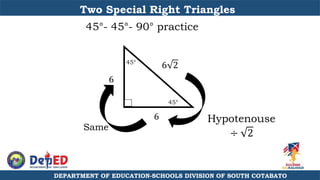
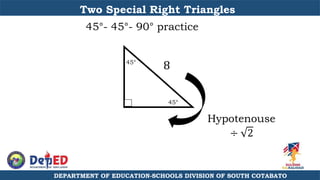
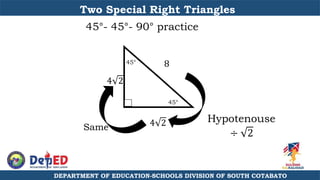
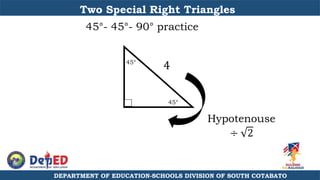
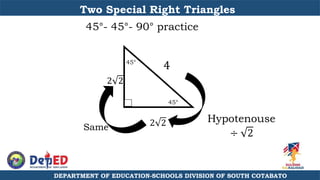
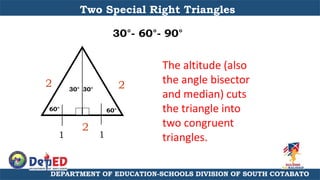
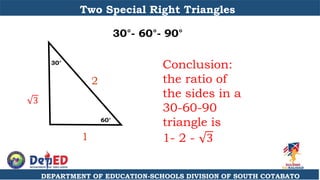
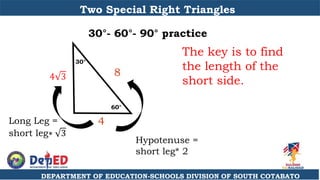
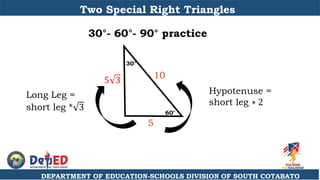
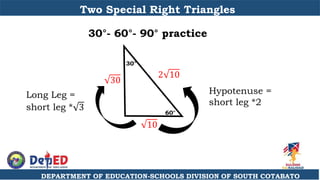
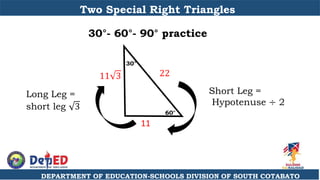
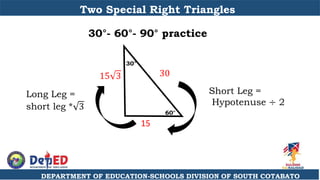
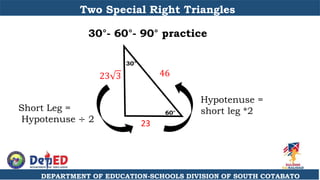
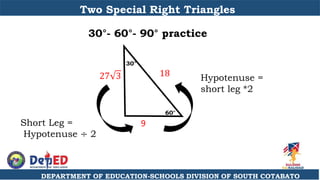
The document discusses a training session for teachers on proving triangle similarities. It will cover identifying similar triangles based on angle-angle, side-side-side, and side-angle-side criteria. Examples are provided to demonstrate proving triangles similar using these three methods. The objectives are for teachers to be able to identify similar triangles, use a similar triangle theorem in a problem, and prove triangles are similar.

1. DIVISION TRAINING OF TEACHERS ON LEAST
LEARNED COMPETENCIES IN MATHEMATICS 9
January 28-29, 2021

2. TRIANGLE SIMILARITIES
ADELAIDA D. OMANIO
Teacher III

3. • At the end of the session, teachers should be able t;
• Identify the similar theorems of triangles ;
• Use or state a specific similar theorem in a given figure and
problems; and
• Prove similar triangles.
PROVING TRIANGLE SIMILARITIES
DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
OBJECTIVES:

4. Proving
Triangles
Similar
(AA~, SSS~, SAS~)
DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
PROVING TRIANGLE SIMILARITIES

5. Similar Triangles
Two triangles are similar if they are the
same shape. That means the vertices
can be paired up so the angles are
congruent. Size does not matter.
PROVING TRIANGLE SIMILARITIES
DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO

6. AA Similarity
(Angle-Angle or AA~)
A  D B  E
If 2 angles of one triangle are congruent to 2 angles of
another triangle, then the triangles are similar.
E
D
A
B
C
F
ABC ~ DEF
Conclusion:
and
Given:
by AA~
PROVING TRIANGLE SIMILARITIES
DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO

7. SSS Similarity
(Side-Side-Side or SSS~)
ABC ~ DEF
If the lengths of the corresponding sides of 2
triangles are proportional, then the triangles are
similar. E
D
A
B
C
F
Given:
Conclusion:

BC
EF
AB
DE

AC
DF
by SSS~
PROVING TRIANGLE SIMILARITIES
DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO

8. E
D
A
B
C
F
5
11
22
8 16
10
Example: SSS Similarity
(Side-Side-Side)
Given: Conclusion:
ABC ~ DEF

BC
EF
AB
DE

AC
DF

8
16
5
10

11
22
By SSS ~
DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
PROVING TRIANGLE SIMILARITIES

9. E
D
A
B
C
F
SAS Similarity
(Side-Angle-Side or SAS~)
ABC ~ DEF
∠𝐴 ≅ ∠𝐷𝑎𝑛𝑑
𝐴𝐵
𝐷𝐸
=
𝐴𝐶
𝐷𝐹
If the lengths of 2 sides of a triangle are proportional to the
lengths of 2 corresponding sides of another triangle and the
included angles are congruent, then the triangles are similar.
Given:
Conclusion: by SAS~
DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
PROVING TRIANGLE SIMILARITIES

10. E
D
A
B
C
F
Example: SAS Similarity
(Side-Angle-Side)
Given: Conclusion: ABC ~ DEF
A  D
AB
DE

AC
DF
5
11 22
10
By SAS~
DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
PROVING TRIANGLE SIMILARITIES

11. A
B C
D E
80
80
ABC ~ ADE by AA ~ Postulate
DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
PROVING TRIANGLE SIMILARITIES

12. A B
C
D E
CDE~ CAB by SAS ~ Theorem
6
3
10
5
DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
PROVING TRIANGLE SIMILARITIES

13. O
N
L
K M
KLM~ KON by SSS ~ Theorem
6
3
10
5
6
6
DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
PROVING TRIANGLE SIMILARITIES

14. C
B
A
D
ACB~ DCA by SSS ~ Theorem
24
36
20
30
16
DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
PROVING TRIANGLE SIMILARITIES

15. N
L
A
P
LNP~ ANL by SAS ~ Theorem
25 9
15
DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
PROVING TRIANGLE SIMILARITIES

16. Similarity is reflexive, symmetric, and transitive.
1. Mark the Given.
2. Mark …
Reflexive (shared) Angles or Vertical Angles
3. Choose a Method. (AA~, SSS~, SAS~)
Think about what you need for the chosen
method and be sure to include those parts in the
proof.
Steps for proving triangles similar:
Proving Triangles Similar
DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
PROVING TRIANGLE SIMILARITIES

17. Problem #1 𝐺𝑖𝑣𝑒𝑛: 𝐷𝐸 ∥ 𝐹𝐺
Pr 𝑜 𝑣𝑒:△ 𝐷𝐸𝐶 ∼ △ 𝐹𝐺𝐶
C
D
E
G
F
Step 1: Mark the given … and what it implies
Step 2: Mark the vertical angles
Step 3: Choose a method: (AA,SSS,SAS)
Step 4: List the Parts in the order of the method with reasons
Step 5: Is there more?
Statements Reasons
Given
Alternate Interior <s
AA Similarity
Alternate Interior <s
1. 𝐷𝐸 ∥ 𝐹𝐺
2. ∠𝐷 ≅ ∠𝐹
3. ∠𝐸 ≅ ∠𝐺
4.△ 𝐷𝐸𝐶 ∼△ 𝐹𝐺𝐶
AA
DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
PROVING TRIANGLE SIMILARITIES

18. Problem #2
Step 1: Mark the given … and what it implies
Step 2: Choose a method: (AA,SSS,SAS)
Step 3: List the Parts in the order of the method with reasons
Step 4: Is there more?
Statements Reasons
Given
Division Property
SSS Similarity
Substitution
SSS
𝐺𝑖𝑣𝑒𝑛: 𝐼𝐽 = 3𝐿𝑁 𝐽𝐾 = 3𝑁𝑃 𝐼𝐾 = 3𝐿𝑃
Pr 𝑜 𝑣𝑒:△ 𝐼𝐽𝐾 ∼△ 𝐿𝑁𝑃
N
L
P
I
J K
1. IJ = 3LN; JK = 3NP; IK = 3LP
2.
IJ
LN
=3,
JK
NP
=3,
IK
LP
=3
3.
IJ
LN
=
JK
NP
=
IK
LP
4. IJK~ LNP
DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
PROVING TRIANGLE SIMILARITIES

19. Problem #3
Step 1: Mark the given … and what it implies
Step 3: Choose a method: (AA,SSS,SAS)
Step 4: List the Parts in the order of the method with reasons
Next Slide………….
Step 5: Is there more?
SAS
𝐺𝑖𝑣𝑒𝑛: 𝐺 𝑖𝑠 𝑡ℎ𝑒 midpoint 𝑜𝑓 𝐸𝐷
𝐻 𝑖𝑠 𝑡ℎ𝑒 midpoint 𝑜𝑓 𝐸𝐹. Prove:△ 𝐸𝐺𝐻 ∼△ 𝐸𝐷𝐹
E
D
F
G H
Step 2: Mark the reflexive angles
DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
PROVING TRIANGLE SIMILARITIES

20. Statements Reasons
7. GEHDEF
8. EGH~ EDF
6.
ED
EG
=
EF
EH
5.
ED
EG
=2 and
EF
EH
=2
DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
PROVING TRIANGLE SIMILARITIES
1. G is the Midpoint of 𝐸𝐷
H is the Midpoint of 𝐸𝐹
2. EG = DG and EH = HF
1. Given
2. Def. of Midpoint
3. ED=EG+GD and EF=EH+HF
4. ED = 2 EG and EF = 2 EH
5.
6.
7.
8.
3. Segment Addition Post.
4. Substitution
6. Substitution
5. Division Property
7. Reflexive Property
8. SAS Postulate

21. Similarity is reflexive,
symmetric, and transitive.
DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
PROVING TRIANGLE SIMILARITIES

22. Choose a Problem.
Problem #1
Problem #2
Problem #3
End Slide Show
SSS
SAS
AA
C
E
G
F
D
E
D
F
G H
P
N
L
I
J K
DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
PROVING TRIANGLE SIMILARITIES

23. Choose a Problem.
Problem #1
Problem #2
Problem #3
End Slide Show
SSS
SAS
AA
C
E
G
F
D
E
D
F
G H
P
N
L
I
J K
DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
PROVING TRIANGLE SIMILARITIES

24. Choose a Problem.
Problem #1
Problem #2
Problem #3
End Slide Show
SSS
SAS
AA
C
E
G
F
D
E
D
F
G H
P
N
L
I
J K
DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
PROVING TRIANGLE SIMILARITIES

25. Choose a Problem.
Problem #1
Problem #2
Problem #3
End Slide Show
SSS
SAS
AA
C
E
G
F
D
E
D
F
G H
P
N
L
I
J K
DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
PROVING TRIANGLE SIMILARITIES

26. The End
1. Mark the Given.
2. Mark …
Shared Angles or Vertical Angles
3. Choose a Method. (AA, SSS , SAS)
**Think about what you need for the chosen method
and be sure to include those parts in the proof.**
DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
PROVING TRIANGLE SIMILARITIES

27. Similar Right Triangles
Geometry
DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO

28. DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
Similar Right Triangles
Objectives
• Solve problems involving similar right triangles
formed by the altitude drawn to the hypotenuse of a
right triangle.
• Use a geometric mean to solve problems.

29. DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
We start with ΔABC
Similar Right Triangles

30. DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
We draw altitude CD to the
hypotenuse.
Similar Right Triangles

31. DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
This divides the original triangle into
two smaller right triangle:
Similar Right Triangles

32. DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
This divides the original triangle into
two smaller right triangle: ΔDCA
Similar Right Triangles

33. DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
This divides the original triangle into
two smaller right triangle: ΔBDC
Similar Right Triangles

34. DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
There are a three triangles in the
figure below.
Similar Right Triangles

35. Big
Medium
Small
Similar Right Triangles
DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO

36. Big Medium
Small
We orient the three triangles to see
the them clearer
Similar Right Triangles
DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO

37. Big Medium
We can see that the three triangles are
similar to each other.
~ ~
Small
Similar Right Triangles
DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO

38. Ex. 1: Finding the Height of a Roof
• Roof Height. A roof has a cross
section that is a right angle. The
diagram shows the approximate
dimensions of this cross section.
• A. Identify the similar triangles.
• B. Find the height h of the roof.
Similar Right Triangles
DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO

39. Solution:
• You may find it helpful to
sketch the three similar
triangles so that the
corresponding angles and
sides have the same
orientation. Mark the
congruent angles. Notice
that some sides appear in
more than one triangle. For
instance XY is the
hypotenuse in ∆XYW and
the shorter leg in ∆XZY.
h
3.1 m
Y
X W
h
5.5 m
Z
Y W
5.5 m
3.1 m
6.3 m
Z
X Y
∆XYW ~ ∆YZW ~ ∆XZY.
Similar Right Triangles
DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO

40. Solution for b.
• Use the fact that ∆XYW ~ ∆XZY to write a
proportion.
YW
ZY
=
XY
XZ
h
5.5
=
3.1
6.3
6.3h = 5.5(3.1)
h ≈ 2.7
The height of the roof is about 2.7 meters.
Corresponding side lengths are in
proportion.
Substitute values.
Cross Product property
Solve for unknown h.
Similar Right Triangles
DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO

41. Geometric Mean Theorems
• Theorem 9.2: In a right triangle, the
altitude from the right angle to the
hypotenuse divides the hypotenuse into
two segments. The length of the altitude
is the geometric mean of the lengths of
the two segments
• Theorem 9.3: In a right triangle, the
altitude from the right angle to the
hypotenuse divides the hypotenuse into
two segments. The length of each leg of
the right triangle is the geometric mean
of the lengths of the hypotenuse and the
segment of the hypotenuse that is
adjacent to the leg.
A
C
B
D
BD
CD
= CD
AD
AB
CB
=
CB
DB
AB
AC
=
AC
AD
Similar Right Triangles
DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO

42. What does that mean?
6
x
=
x
3
5 + 2
y
=
y
2
3
6
x y 5
2
18 = x2
√18 = x
√9 ∙ √2 = x
3 √2 = x
14 = y2
7
y
=
y
2
√14 = y
Similar Right Triangles
DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO

43. Two Special Right Triangles
45°- 45°- 90°
30°- 60°- 90°
DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO

44. Two Special Right Triangles
45°- 45°- 90°
The 45-45-90
triangle is
based on the
square with
sides of 1 unit.
1
1
1
1
DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO

45. Two Special Right Triangles
45°- 45°- 90°
If we draw the
diagonals we
form two
45-45-90
triangles.
1
1
1
1
45°
45°
45°
45°
90°
90°
DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO

46. DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH
Two Special Right Triangles
45°- 45°- 90°
Conclusion:
the ratio of
the sides in a
45-45-90
triangle is
1-1- 2
1
1
45°
45°
2

47. DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
Two Special Right Triangles
45°- 45°- 90° practice
4
4
45°
45°
4 2
leg* 2
Same

48. DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
Two Special Right Triangles
45°- 45°- 90° practice
9
9
45°
45°
9 2
leg* 2
Same

49. DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
Two Special Right Triangles
45°- 45°- 90° practice
2
2
45°
45°
2 2
leg* 2
Same

50. DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
Two Special Right Triangles
45°- 45°- 90° practice
7
45°
45°
leg* 2
Same
7
14

51. DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
Two Special Right Triangles
45°- 45°- 90° practice
Now let’s go backwards!

52. DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
Two Special Right Triangles
45°- 45°- 90° practice
45°
45°
Hypotenouse
÷ 2
3 2

53. DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
Two Special Right Triangles
45°- 45°- 90° practice
3 2
2
= 3

54. DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
Two Special Right Triangles
45°- 45°- 90° practice
3
45°
45°
Same
3
3 2
Hypotenouse
÷ 2

55. DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
Two Special Right Triangles
45°- 45°- 90° practice
45°
45°
6 2
Hypotenouse
÷ 2

56. DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
Two Special Right Triangles
45°- 45°- 90° practice
6 2
2
= 6

57. DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
Two Special Right Triangles
45°- 45°- 90° practice
6
45°
45°
Same
6
6 2
Hypotenouse
÷ 2

58. DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
Two Special Right Triangles
45°- 45°- 90° practice
45°
45°
8
Hypotenouse
÷ 2

59. DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
Two Special Right Triangles
45°- 45°- 90° practice
8
2
∗
2
2
=
8 2
2
= 4 2

60. DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
Two Special Right Triangles
45°- 45°- 90° practice
4 2
45°
45°
Same 4 2
8
Hypotenouse
÷ 2

61. Two Special Right Triangles
45°- 45°- 90° practice
45°
45°
4
Hypotenouse
÷ 2
DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO

62. Two Special Right Triangles
45°- 45°- 90° practice
4
2
∗
2
2
=
4 2
2
= 2 2
DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO

63. Two Special Right Triangles
45°- 45°- 90° practice
2 2
45°
45°
Same 2 2
4
Hypotenouse
÷ 2
DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO

64. DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
Two Special Right Triangles
30°- 60°- 90°
The 30-60-90
triangle is based
on an equilateral
triangle with
sides of 2 units.
2
2
2
60°
60°

65. DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
Two Special Right Triangles
30°- 60°- 90°
The altitude (also
the angle bisector
and median) cuts
the triangle into
two congruent
triangles.
2
2
2
60°
60°
30° 30°
1 1

66. DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
Two Special Right Triangles
30°- 60°- 90°
This creates
the 30-60-90
triangle with a
hypotenuse a
short leg and
a long leg.
60°
30°
Long
leg
Short leg

67. DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
Two Special Right Triangles
30°- 60°- 90° practice
We saw that the
hypotenuse is
twice the short leg.
We can use the
Pythagorean
Theorem to find
the long leg.
60°
30°
2

68. DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
Two Special Right Triangles
30°- 60°- 90°
Conclusion:
the ratio of
the sides in a
30-60-90
triangle is
1- 2 - 3
60°
30°
2
3
1

69. DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
Two Special Right Triangles
30°- 60°- 90° practice
60°
30°
8
The key is to find
the length of the
short side.
4 3
4
Hypotenuse =
short leg* 2
Long Leg =
short leg∗ 3

70. DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
Two Special Right Triangles
30°- 60°- 90° practice
60°
30°
10
5 3
5
Hypotenuse =
short leg ∗ 2
Long Leg =
short leg * 3

71. DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
Two Special Right Triangles
30°- 60°- 90° practice
60°
30°
2 10
30
10
Hypotenuse =
short leg *2
Long Leg =
short leg * 3

72. DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
Two Special Right Triangles
30°- 60°- 90° practice
60°
30°
22
11 3
11
Short Leg =
Hypotenuse ÷ 2
Long Leg =
short leg 3

73. DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
Two Special Right Triangles
30°- 60°- 90° practice
60°
30°
30
15 3
15
Short Leg =
Hypotenuse ÷ 2
Long Leg =
short leg * 3

74. DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
Two Special Right Triangles
30°- 60°- 90° practice
60°
30°
46
23 3
23
Short Leg =
Hypotenuse ÷ 2
Hypotenuse =
short leg *2

75. DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
Two Special Right Triangles
30°- 60°- 90° practice
60°
30°
18
27 3
9
Short Leg =
Hypotenuse ÷ 2
Hypotenuse =
short leg *2

76. DEPARTMENT OF EDUCATION-SCHOOLS DIVISION OF SOUTH COTABATO
Two Special Right Triangles
The End