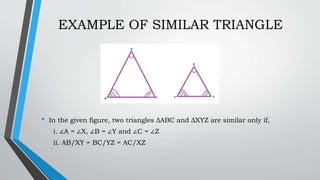
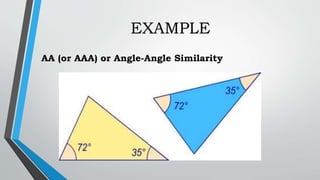
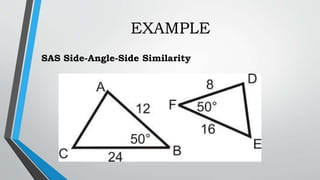
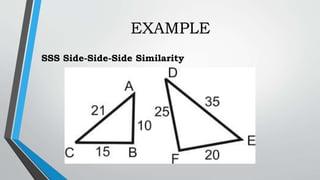
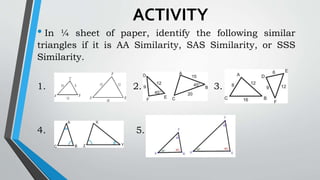
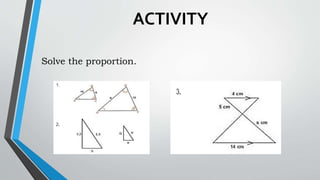
This document discusses similar triangles and their properties. It begins with an opening prayer and review of past lessons. Then it presents an activity to play a "Try Not to Laugh" game in groups and earn additional points for a quiz. The objectives are presented, which are to investigate properties of similar triangles using ratios and proportions, compare similar and congruent triangles, and prove conditions of similarity. It defines similar triangles as those with the same shape but varying sizes, having equal corresponding angles and proportional corresponding sides. It presents the AA, SAS and SSS similarity theorems and examples. Properties, formulas and a comparison of similar and congruent triangles are discussed. An activity is assigned to identify given triangles as AA, SAS or SSS similar

1. Similar
Triangles
Prepared by: Ms. Roei Patrice Jewel Garcia

2. Prayer
• “Dear Lord and Father of all, Thank you for today. Thank you
for ways in which you provide for us all. For Your protection
and love we thank you. Help us to focus our hearts and minds
now on what we are about to learn. Inspire us by Your Holy
Spirit as we listen and write. Guide us by your eternal light as
we discover more about the world around us. We ask all this in
the name of Jesus. Amen.”

3. REWIEW OFTHE
PAST LESSON

4. ACTIVITY
“Try not to Laugh Challenge
• The class will be divided into 4 groups, and they will select a leader
on each group.
• The mechanics of the game is that they should try not to laugh,
smirk, nor smile, each member of the group should be
emotionless for 5 seconds while watching pictures presented on the
PowerPoint.
• Now, each group is given 10 points from the beginning of
the game, and the leaders of each group should watch
carefully and observe other groups if they laugh or smirk or smile,
and if they do so, 1 point will be deducted to their group on each
round.
• This game consists 5 rounds. And the points earned for this game
will be the additional points for the coming quiz.

5. PICTURE #1

6. PICTURE #2

7. PICTURE #3

8. PICTURE #4

9. PICTURE # 5

10. PICTURE #6

11. OBJECTIVES
At the end of the lesson, learners are expected to:
1. investigate the properties of similar triangles using
their prior knowledge of ratio and proportion;
2. compare the properties of similar triangles and
congruent triangles; and
3. prove the conditions of triangle similarities
and apply it in order to solve problems.

12. WHAT IS SIMILARITY OFTRIANGLES?
• Similar triangles are triangles that have the same
shape, but their sizes may vary. All equilateral
triangles, squares of any side lengths are examples of
similar objects. In other words, if two triangles are
similar, then their corresponding angles are
congruent and corresponding sides are in equal
proportion. We denote the similarity of triangles here
by ‘~’ symbol.

13. WHAT IS SIMILARITY OFTRIANGLES?
• Two triangles are similar if they have the same ratio of
corresponding sides and equal pair of corresponding
angles. If two or more figures have the same
shape, but their sizes are different, then such
objects are called similar figures. Consider a hula
hoop and wheel of a cycle, the shapes of both these
objects are similar to each other as their shapes are
the same.

14. EXAMPLE OF SIMILAR TRIANGLE
• In the given figure, two triangles ΔABC and ΔXYZ are similar only if,
i. ∠A = ∠X, ∠B = ∠Y and ∠C = ∠Z
ii. AB/XY = BC/YZ = AC/XZ

15. PROPERTIES OF SIMILARITY OF
TRIANGLES
Both have the same shape but sizes may be different.
Each pair of corresponding angles are equal.
The ratio of corresponding sides is the same.

16. Formula for Similarity of Triangles
•∠A = ∠X, ∠B = ∠Y and ∠C = ∠Z
•AB/XY = BC/YZ = AC/XZ

17. COMPARISON OF SIMILAR TRIANGLES
AND CONGRUENT TRIANGLES

18. SIMILAR TRIANGLES THEOREMS
AA (or AAA) or Angle-Angle Similarity
• If any two angles of a triangle are equal to any two angles of
another triangle, then the two triangles are similar to each other.
From the figure given above, if ∠ A = ∠X and ∠C = ∠Z then
ΔABC~ΔXYZ.
From the result obtained, we can easily say that,
AB/XY = BC/YZ = AC/XZ and ∠B = ∠Y

19. EXAMPLE
AA (or AAA) or Angle-Angle Similarity

20. SIMILAR TRIANGLES THEOREMS
SAS or Side-Angle-Side Similarity
• If the two sides of a triangle are in the same proportion
of the two sides of another triangle, and the angle
inscribed by the two sides in both the triangle are equal,
then two triangles are said to be similar.
Thus, if ∠A = ∠X and AB/XY = AC/XZ then ΔABC ~ΔXYZ.
From the congruency, AB/XY = BC/YZ = AC/XZ and ∠B
= ∠Y and ∠C = ∠Z

21. EXAMPLE
SAS Side-Angle-Side Similarity

22. SIMILAR TRIANGLES THEOREMS
SSS or Side-Side-Side Similarity
• If all the three sides of a triangle are in proportion to
the three sides of another triangle, then the two triangles
are similar.
Thus, if AB/XY = BC/YZ = AC/XZ then ΔABC ~ΔXYZ.
From this result, we can infer that-∠A = ∠X, ∠B = ∠Y and
∠C = ∠Z

23. EXAMPLE
SSS Side-Side-Side Similarity

24. Remember that...
• Similar Triangles – triangles are similar if and only if their
corresponding angles are congruent and their corresponding
sides are proportional.
• AA Similarity Theorem - If two angles of a triangle are
congruent to the two angles of the second triangle respectively,
then the two triangles are similar.
• SAS Similarity Theorem - If two pairs of corresponding sides
of two triangles are proportional and the included angles are
congruent then the two triangles are similar.
• SSS Similarity Theorem - If the corresponding sides of two
triangles are proportional then the two triangles are similar.

25. ACTIVITY
• In ¼ sheet of paper, identify the following similar
triangles if it is AA Similarity, SAS Similarity, or SSS
Similarity.
1. 2. 3.
4. 5.

26. ACTIVITY
Solve the proportion.

27. ASSIGNMENT
Study in advance the Theorems on Triangle
Similarity (Basic Proportionality Theorem
and Angle Bisector Theorem).