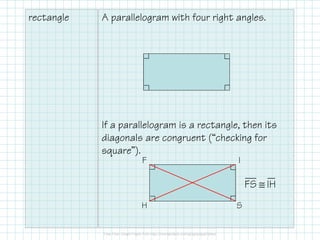
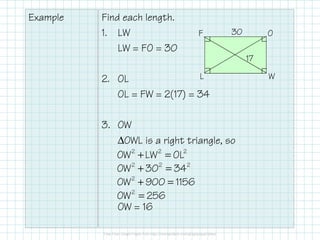
The document discusses the properties and proofs related to special parallelograms, specifically rectangles, rhombuses, and squares. It outlines their characteristics, such as angles and side congruency, and provides methods to prove a quadrilateral is a specific type of parallelogram. Additionally, it includes examples and problem-solving applications relevant to these geometric shapes.

1. Obj. 26 Special Parallelograms
The student is able to (I can):
• Prove and apply properties of rectangles, rhombuses, and
squares.
• Use properties of rectangles, rhombuses, and squares to
solve problems.
• Prove that a given quadrilateral is a rectangle, rhombus,
or square.

2. rectangle
A parallelogram with four right angles.
If a parallelogram is a rectangle, then its
diagonals are congruent (“checking for
square”).
F
I
FS ≅ IH
H
S

3. Because a rectangle is a parallelogram, it
also “inherits” all of the properties of a
parallelogram:
• Opposite sides parallel
• Opposite sides congruent
• Opposite angles congruent (actually all
angles are congruent)
• Consecutive angles supplementary
• Diagonals bisect each other

4. Example
Find each length.
1. LW
LW = FO = 30
F
30
O
17
L
2. OL
OL = FW = 2(17) = 34
3. OW
∆OWL is a right triangle, so
OW 2 + LW 2 = OL2
OW 2 + 302 = 34 2
OW 2 + 900 = 1156
OW 2 = 256
OW = 16
W

5. rhombus
A parallelogram with four congruent sides.
If a parallelogram is a rhombus, then its
diagonals are perpendicular.

6. Proof:
B
O
S
L
W
Because BOWL is a rhombus, BO ≅ OW.
Diagonals bisect each other, so BS ≅ WS.
The reflexive property means that OS ≅ OS.
Therefore, ∆OSB ≅ ∆OSW by SSS. This
means that ∠OSB ≅ ∠OSW. Since they
are also supplementary, they must be 90º.

7. If a parallelogram is a rhombus, then each
diagonal bisects a pair of opposite angles.
3
1 2
8
∠1 ≅ ∠2
∠3 ≅ ∠4
∠5 ≅ ∠6
∠7 ≅ ∠8
7
4
6
5
Since opposite angles are
also congruent:
∠1 ≅ ∠2 ≅ ∠5 ≅ ∠6
∠3 ≅ ∠4 ≅ ∠7 ≅ ∠8

8. Examples
1. What is the perimeter of a rhombus
whose side length is 7?
4(7) = 28
2. Find the value of x
The side = 10
Pyth. triple: 6, 8, 10
x=6
Perimeter = 40
(13y—9)º
3. Find the value of y
13y — 9 = 3y + 11
10y = 20
y=2
x
10
8
(3y+11)º

9. square
A quadrilateral with four right angles and
four congruent sides.
Note: A square has all of the properties of
both a rectangle and a rhombus:
• Diagonals are congruent
• Diagonals are perpendicular
• Diagonals bisect opposite angles.

10. Conditions for
Special
Parallelograms
You can always use the definitions to
prove these, but there are also some
shortcuts we can use. For all of these
shortcuts, we must first prove or know
that the quadrilateral is a parallelogram.
• To prove a parallelogram is a rectangle
(pick one):
— One angle is a right angle
— The diagonals are congruent

11. • To prove a parallelogram is a rhombus
(pick one):
— A pair of consecutive sides is
congruent
— The diagonals are perpendicular
— One diagonal bisects a pair of
opposite angles
• To prove that a quadrilateral is a
square:
— It is both a rectangle and a rhombus.