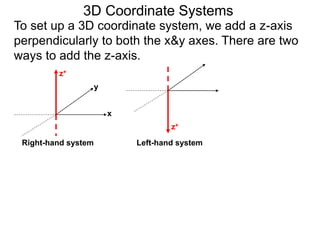
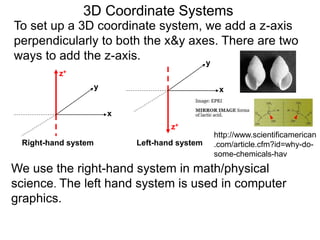
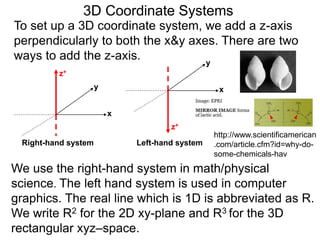
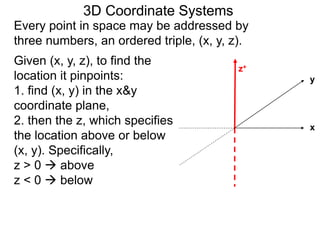
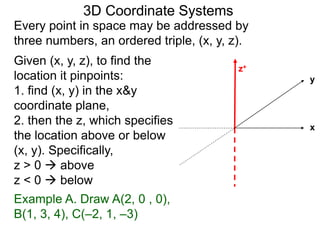
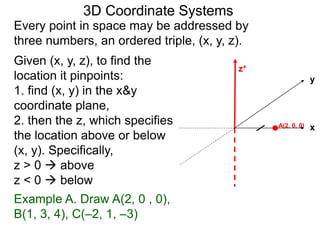
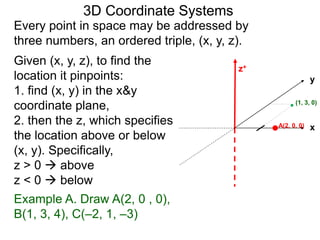
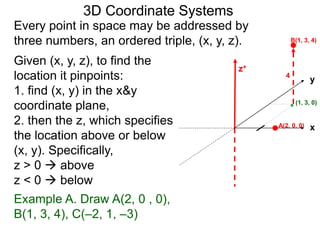
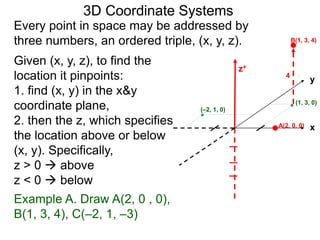
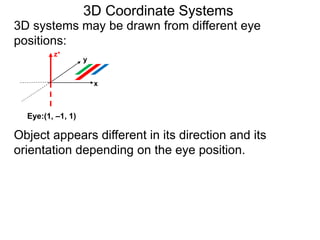
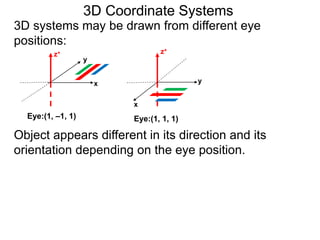
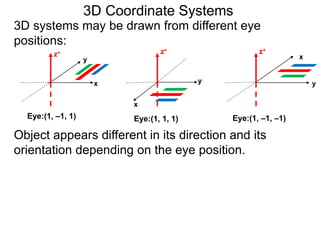
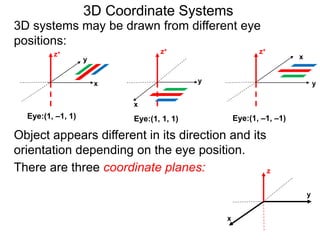
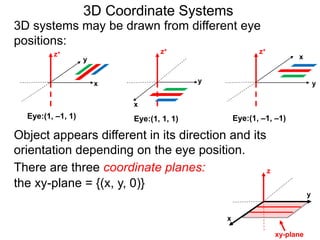
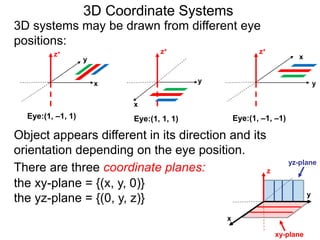
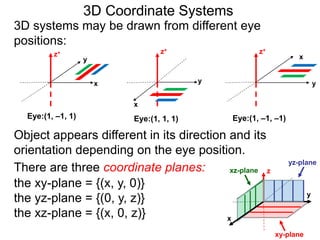
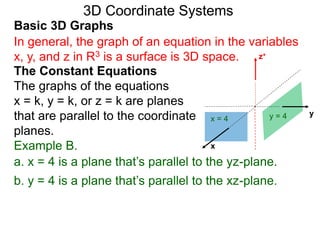
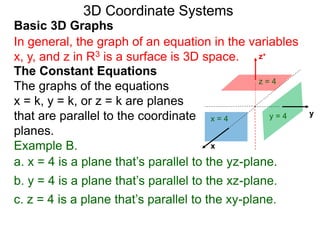
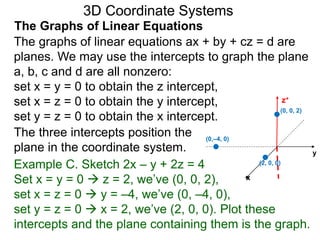
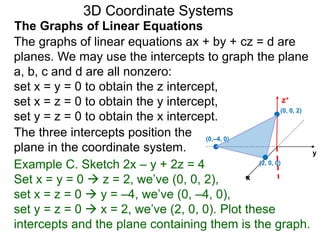
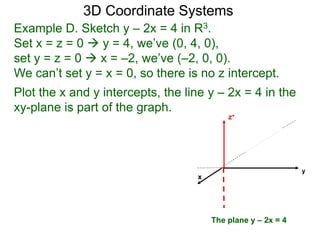
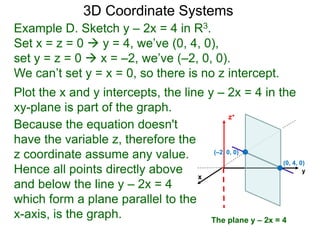
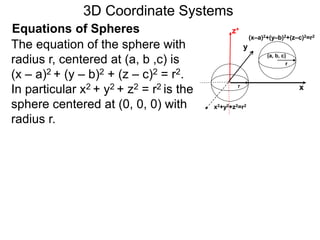
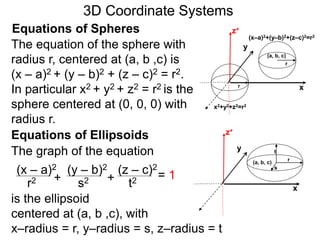
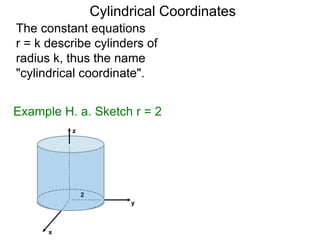
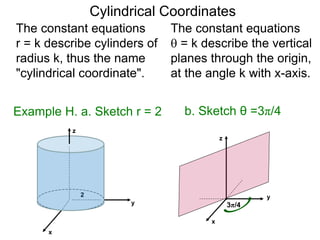
The document discusses 3D coordinate systems. It explains that a 3D coordinate system adds a z-axis perpendicular to the x- and y-axes. There are two ways to orient the z-axis, resulting in right-hand and left-hand systems. Points in 3D space are identified by ordered triples (x,y,z). Graphs of equations in 3D are surfaces. Constant equations like x=k form planes parallel to coordinate planes.

1. 3D Coordinate Systems

2. 3D Coordinate Systems
To set up a 3D coordinate system, we add a z-axis
perpendicularly to both the x&y axes.

3. 3D Coordinate Systems
To set up a 3D coordinate system, we add a z-axis
perpendicularly to both the x&y axes. There are two
ways to add the z-axis.

4. 3D Coordinate Systems
To set up a 3D coordinate system, we add a z-axis
perpendicularly to both the x&y axes. There are two
ways to add the z-axis.
x
y
z+
Right-hand system

5. 3D Coordinate Systems
To set up a 3D coordinate system, we add a z-axis
perpendicularly to both the x&y axes. There are two
ways to add the z-axis.
x
y
z+
z+
Right-hand system Left-hand system

6. 3D Coordinate Systems
To set up a 3D coordinate system, we add a z-axis
perpendicularly to both the x&y axes. There are two
ways to add the z-axis.
x
y
z+
x
y
z+
Right-hand system Left-hand system

7. 3D Coordinate Systems
To set up a 3D coordinate system, we add a z-axis
perpendicularly to both the x&y axes. There are two
ways to add the z-axis.
x
y
z+
x
y
z+
Right-hand system Left-hand system
http://www.scientificamerican
.com/article.cfm?id=why-do-
some-chemicals-hav

8. 3D Coordinate Systems
We use the right-hand system in math/physical
science. The left hand system is used in computer
graphics.
To set up a 3D coordinate system, we add a z-axis
perpendicularly to both the x&y axes. There are two
ways to add the z-axis.
x
y
z+
x
y
z+
Right-hand system Left-hand system
http://www.scientificamerican
.com/article.cfm?id=why-do-
some-chemicals-hav

9. 3D Coordinate Systems
We use the right-hand system in math/physical
science. The left hand system is used in computer
graphics. The real line which is 1D is abbreviated as R.
We write R2 for the 2D xy-plane and R3 for the 3D
rectangular xyz–space.
To set up a 3D coordinate system, we add a z-axis
perpendicularly to both the x&y axes. There are two
ways to add the z-axis.
x
y
z+
x
y
z+
Right-hand system Left-hand system
http://www.scientificamerican
.com/article.cfm?id=why-do-
some-chemicals-hav

10. Every point in space may be addressed by
three numbers, an ordered triple, (x, y, z).
3D Coordinate Systems
y
z+
x

11. Every point in space may be addressed by
three numbers, an ordered triple, (x, y, z).
Given (x, y, z), to find the
location it pinpoints:
3D Coordinate Systems
y
z+
x

12. Every point in space may be addressed by
three numbers, an ordered triple, (x, y, z).
Given (x, y, z), to find the
location it pinpoints:
1. find (x, y) in the x&y
coordinate plane,
3D Coordinate Systems
y
z+
x

13. Every point in space may be addressed by
three numbers, an ordered triple, (x, y, z).
Given (x, y, z), to find the
location it pinpoints:
1. find (x, y) in the x&y
coordinate plane,
2. then the z, which specifies
the location above or below
(x, y). Specifically,
z > 0  above
z < 0  below
3D Coordinate Systems
y
z+
x

14. Every point in space may be addressed by
three numbers, an ordered triple, (x, y, z).
Given (x, y, z), to find the
location it pinpoints:
1. find (x, y) in the x&y
coordinate plane,
2. then the z, which specifies
the location above or below
(x, y). Specifically,
z > 0  above
z < 0  below
Example A. Draw A(2, 0 , 0),
B(1, 3, 4), C(–2, 1, –3)
3D Coordinate Systems
y
z+
x

15. y
z+
Example A. Draw A(2, 0 , 0),
B(1, 3, 4), C(–2, 1, –3)
3D Coordinate Systems
xA(2, 0, 0)
Given (x, y, z), to find the
location it pinpoints:
1. find (x, y) in the x&y
coordinate plane,
2. then the z, which specifies
the location above or below
(x, y). Specifically,
z > 0  above
z < 0  below
Every point in space may be addressed by
three numbers, an ordered triple, (x, y, z).

16. y
z+
Example A. Draw A(2, 0 , 0),
B(1, 3, 4), C(–2, 1, –3)
3D Coordinate Systems
xA(2, 0, 0)
(1, 3, 0)
Given (x, y, z), to find the
location it pinpoints:
1. find (x, y) in the x&y
coordinate plane,
2. then the z, which specifies
the location above or below
(x, y). Specifically,
z > 0  above
z < 0  below
Every point in space may be addressed by
three numbers, an ordered triple, (x, y, z).

17. y
z+
Example A. Draw A(2, 0 , 0),
B(1, 3, 4), C(–2, 1, –3)
3D Coordinate Systems
xA(2, 0, 0)
(1, 3, 0)
B(1, 3, 4)
4
Given (x, y, z), to find the
location it pinpoints:
1. find (x, y) in the x&y
coordinate plane,
2. then the z, which specifies
the location above or below
(x, y). Specifically,
z > 0  above
z < 0  below
Every point in space may be addressed by
three numbers, an ordered triple, (x, y, z).

18. y
z+
Example A. Draw A(2, 0 , 0),
B(1, 3, 4), C(–2, 1, –3)
3D Coordinate Systems
xA(2, 0, 0)
(–2, 1, 0)
4
Given (x, y, z), to find the
location it pinpoints:
1. find (x, y) in the x&y
coordinate plane,
2. then the z, which specifies
the location above or below
(x, y). Specifically,
z > 0  above
z < 0  below
Every point in space may be addressed by
three numbers, an ordered triple, (x, y, z).
(1, 3, 0)
B(1, 3, 4)

19. y
z+
Example A. Draw A(2, 0 , 0),
B(1, 3, 4), C(–2, 1, –3)
3D Coordinate Systems
xA(2, 0, 0)
(–2, 1, 0)
4
C(–2, 1, –3)
Given (x, y, z), to find the
location it pinpoints:
1. find (x, y) in the x&y
coordinate plane,
2. then the z, which specifies
the location above or below
(x, y). Specifically,
z > 0  above
z < 0  below
Every point in space may be addressed by
three numbers, an ordered triple, (x, y, z).
(1, 3, 0)
B(1, 3, 4)

20. 3D systems may be drawn from different eye
positions:
3D Coordinate Systems

21. 3D systems may be drawn from different eye
positions:
x
y
z+
Eye:(1, –1, 1)
3D Coordinate Systems
Object appears different in its direction and its
orientation depending on the eye position.

22. 3D systems may be drawn from different eye
positions:
x
y
z+
x
y
z+
Eye:(1, –1, 1) Eye:(1, 1, 1)
3D Coordinate Systems
Object appears different in its direction and its
orientation depending on the eye position.

23. 3D systems may be drawn from different eye
positions:
x
y
z+
x
y
z+
x
y
z+
Eye:(1, –1, 1) Eye:(1, 1, 1) Eye:(1, –1, –1)
3D Coordinate Systems
Object appears different in its direction and its
orientation depending on the eye position.

24. 3D systems may be drawn from different eye
positions:
x
y
z+
x
y
z+
x
y
z+
Eye:(1, –1, 1) Eye:(1, 1, 1) Eye:(1, –1, –1)
x
y
z
3D Coordinate Systems
There are three coordinate planes:
Object appears different in its direction and its
orientation depending on the eye position.

25. 3D systems may be drawn from different eye
positions:
x
y
z+
x
y
z+
x
y
z+
Eye:(1, –1, 1) Eye:(1, 1, 1) Eye:(1, –1, –1)
the xy-plane = {(x, y, 0)}
x
y
z
xy-plane
3D Coordinate Systems
There are three coordinate planes:
Object appears different in its direction and its
orientation depending on the eye position.

26. 3D systems may be drawn from different eye
positions:
x
y
z+
x
y
z+
x
y
z+
Eye:(1, –1, 1) Eye:(1, 1, 1) Eye:(1, –1, –1)
the xy-plane = {(x, y, 0)}
the yz-plane = {(0, y, z)}
x
y
z
xy-plane
yz-plane
3D Coordinate Systems
There are three coordinate planes:
Object appears different in its direction and its
orientation depending on the eye position.

27. 3D systems may be drawn from different eye
positions:
x
y
z+
x
y
z+
x
y
z+
Eye:(1, –1, 1) Eye:(1, 1, 1) Eye:(1, –1, –1)
the xy-plane = {(x, y, 0)}
the yz-plane = {(0, y, z)}
the xz-plane = {(x, 0, z)} x
y
z
xy-plane
xz-plane
3D Coordinate Systems
There are three coordinate planes:
Object appears different in its direction and its
orientation depending on the eye position.
yz-plane

28. Basic 3D Graphs
3D Coordinate Systems

29. Basic 3D Graphs
3D Coordinate Systems
In general, the graph of an equation in the variables
x, y, and z in R3 is a surface is 3D space.

30. Basic 3D Graphs
The Constant Equations
3D Coordinate Systems
In general, the graph of an equation in the variables
x, y, and z in R3 is a surface is 3D space.

31. Basic 3D Graphs
The Constant Equations
The graphs of the equations
x = k, y = k, or z = k are planes
that are parallel to the coordinate
planes.
3D Coordinate Systems
In general, the graph of an equation in the variables
x, y, and z in R3 is a surface is 3D space.

32. Basic 3D Graphs
The Constant Equations
The graphs of the equations
x = k, y = k, or z = k are planes
that are parallel to the coordinate
planes.
3D Coordinate Systems
In general, the graph of an equation in the variables
x, y, and z in R3 is a surface is 3D space.

33. x
z+
a. x = 4 is a plane that’s parallel to the yz-plane.
x = 4
y
Basic 3D Graphs
The Constant Equations
The graphs of the equations
x = k, y = k, or z = k are planes
that are parallel to the coordinate
planes.
3D Coordinate Systems
In general, the graph of an equation in the variables
x, y, and z in R3 is a surface is 3D space.
Example B.

34. x
z+
a. x = 4 is a plane that’s parallel to the yz-plane.
x = 4
b. y = 4 is a plane that’s parallel to the xz-plane.
yy = 4
Basic 3D Graphs
The Constant Equations
The graphs of the equations
x = k, y = k, or z = k are planes
that are parallel to the coordinate
planes.
3D Coordinate Systems
In general, the graph of an equation in the variables
x, y, and z in R3 is a surface is 3D space.
Example B.

35. x
z+
a. x = 4 is a plane that’s parallel to the yz-plane.
x = 4
b. y = 4 is a plane that’s parallel to the xz-plane.
yy = 4
c. z = 4 is a plane that’s parallel to the xy-plane.
z = 4
Basic 3D Graphs
The Constant Equations
The graphs of the equations
x = k, y = k, or z = k are planes
that are parallel to the coordinate
planes.
3D Coordinate Systems
In general, the graph of an equation in the variables
x, y, and z in R3 is a surface is 3D space.
Example B.

36. x
z+
a. x = 4 is a plane that’s parallel to the yz-plane.
x = 4
b. y = 4 is a plane that’s parallel to the xz-plane.
yy = 4
c. z = 4 is a plane that’s parallel to the xy-plane.
z = 4
Basic 3D Graphs
The Constant Equations
The graphs of the equations
x = k, y = k, or z = k are planes
that are parallel to the coordinate
planes.
3D Coordinate Systems
In general, the graph of an equation in the variables
x, y, and z in R3 is a surface is 3D space.
Example B.
d. The graph of (x – 4)(y – 4)(z – 4) = 0 is all three
planes.

37. 3D Coordinate Systems
The Graphs of Linear Equations

38. The graphs of linear equations ax + by + cz = d are
planes.
3D Coordinate Systems
The Graphs of Linear Equations

39. The graphs of linear equations ax + by + cz = d are
planes. We may use the intercepts to graph the plane.
a, b, c and d are all nonzero:
3D Coordinate Systems
The Graphs of Linear Equations

40. The graphs of linear equations ax + by + cz = d are
planes. We may use the intercepts to graph the plane
a, b, c and d are all nonzero:
set x = y = 0 to obtain the z intercept,
set x = z = 0 to obtain the y intercept,
set y = z = 0 to obtain the x intercept.
3D Coordinate Systems
The Graphs of Linear Equations

41. The graphs of linear equations ax + by + cz = d are
planes. We may use the intercepts to graph the plane
a, b, c and d are all nonzero:
set x = y = 0 to obtain the z intercept,
set x = z = 0 to obtain the y intercept,
set y = z = 0 to obtain the x intercept.
3D Coordinate Systems
The Graphs of Linear Equations
The three intercepts position the
plane in the coordinate system.

42. The graphs of linear equations ax + by + cz = d are
planes. We may use the intercepts to graph the plane
a, b, c and d are all nonzero:
set x = y = 0 to obtain the z intercept,
set x = z = 0 to obtain the y intercept,
set y = z = 0 to obtain the x intercept.
Example C. Sketch 2x – y + 2z = 4.
3D Coordinate Systems
The Graphs of Linear Equations
The three intercepts position the
plane in the coordinate system.

43. x
z+
The graphs of linear equations ax + by + cz = d are
planes. We may use the intercepts to graph the plane
a, b, c and d are all nonzero:
set x = y = 0 to obtain the z intercept,
set x = z = 0 to obtain the y intercept,
set y = z = 0 to obtain the x intercept.
Example C. Sketch 2x – y + 2z = 4
Set x = y = 0  z = 2, we’ve (0, 0, 2),
y
3D Coordinate Systems
The Graphs of Linear Equations
The three intercepts position the
plane in the coordinate system.

44. x
z+
The graphs of linear equations ax + by + cz = d are
planes. We may use the intercepts to graph the plane
a, b, c and d are all nonzero:
set x = y = 0 to obtain the z intercept,
set x = z = 0 to obtain the y intercept,
set y = z = 0 to obtain the x intercept.
Example C. Sketch 2x – y + 2z = 4
Set x = y = 0  z = 2, we’ve (0, 0, 2),
set x = z = 0  y = –4, we’ve (0, –4, 0),
set y = z = 0  x = 2, we’ve (2, 0, 0).
y
3D Coordinate Systems
The Graphs of Linear Equations
The three intercepts position the
plane in the coordinate system.

45. x
z+
The graphs of linear equations ax + by + cz = d are
planes. We may use the intercepts to graph the plane
a, b, c and d are all nonzero:
set x = y = 0 to obtain the z intercept,
set x = z = 0 to obtain the y intercept,
set y = z = 0 to obtain the x intercept.
Example C. Sketch 2x – y + 2z = 4
Set x = y = 0  z = 2, we’ve (0, 0, 2),
set x = z = 0  y = –4, we’ve (0, –4, 0),
set y = z = 0  x = 2, we’ve (2, 0, 0). Plot these
intercepts and the plane containing them is the graph.
y
3D Coordinate Systems
The Graphs of Linear Equations
The three intercepts position the
plane in the coordinate system.
(0,–4, 0)
(2, 0, 0)
(0, 0, 2)

46. x
z+
The graphs of linear equations ax + by + cz = d are
planes. We may use the intercepts to graph the plane
a, b, c and d are all nonzero:
set x = y = 0 to obtain the z intercept,
set x = z = 0 to obtain the y intercept,
set y = z = 0 to obtain the x intercept.
Example C. Sketch 2x – y + 2z = 4
Set x = y = 0  z = 2, we’ve (0, 0, 2),
set x = z = 0  y = –4, we’ve (0, –4, 0),
set y = z = 0  x = 2, we’ve (2, 0, 0). Plot these
intercepts and the plane containing them is the graph.
y
3D Coordinate Systems
The Graphs of Linear Equations
The three intercepts position the
plane in the coordinate system.
(0, 0, 2)
(0,–4, 0)
(2, 0, 0)

47. Example D. Sketch y – 2x = 4 in R3.
3D Coordinate Systems

48. Example D. Sketch y – 2x = 4 in R3.
Set x = z = 0  y = 4, we’ve (0, 4, 0),
set y = z = 0  x = –2, we’ve (–2, 0, 0).
3D Coordinate Systems

49. Example D. Sketch y – 2x = 4 in R3.
Set x = z = 0  y = 4, we’ve (0, 4, 0),
set y = z = 0  x = –2, we’ve (–2, 0, 0).
We can’t set y = x = 0, so there is no z intercept.
3D Coordinate Systems

50. Example D. Sketch y – 2x = 4 in R3.
Set x = z = 0  y = 4, we’ve (0, 4, 0),
set y = z = 0  x = –2, we’ve (–2, 0, 0).
We can’t set y = x = 0, so there is no z intercept.
Plot the x and y intercepts, the line y – 2x = 4 in the
xy-plane is part of the graph.
3D Coordinate Systems

51. x
z+
Example D. Sketch y – 2x = 4 in R3.
Set x = z = 0  y = 4, we’ve (0, 4, 0),
set y = z = 0  x = –2, we’ve (–2, 0, 0).
We can’t set y = x = 0, so there is no z intercept.
Plot the x and y intercepts, the line y – 2x = 4 in the
xy-plane is part of the graph.
3D Coordinate Systems
The plane y – 2x = 4
y

52. x
z+
Example D. Sketch y – 2x = 4 in R3.
Set x = z = 0  y = 4, we’ve (0, 4, 0),
set y = z = 0  x = –2, we’ve (–2, 0, 0).
We can’t set y = x = 0, so there is no z intercept.
Plot the x and y intercepts, the line y – 2x = 4 in the
xy-plane is part of the graph.
3D Coordinate Systems
The plane y – 2x = 4
y
(0, 4, 0)
(–2, 0, 0)

53. x
z+
Example D. Sketch y – 2x = 4 in R3.
Set x = z = 0  y = 4, we’ve (0, 4, 0),
set y = z = 0  x = –2, we’ve (–2, 0, 0).
We can’t set y = x = 0, so there is no z intercept.
Because the equation doesn't
have the variable z, therefore the
z coordinate can assume any
value.
Plot the x and y intercepts, the line y – 2x = 4 in the
xy-plane is part of the graph.
3D Coordinate Systems
The plane y – 2x = 4
y
(0, 4, 0)
(–2, 0, 0)

54. x
z+
Example D. Sketch y – 2x = 4 in R3.
Set x = z = 0  y = 4, we’ve (0, 4, 0),
set y = z = 0  x = –2, we’ve (–2, 0, 0).
We can’t set y = x = 0, so there is no z intercept.
Because the equation doesn't
have the variable z, therefore the
z coordinate assume any value.
Hence all points directly above
and below the line y – 2x = 4,
which form a plane parallel to the
z-axis, is the graph.
Plot the x and y intercepts, the line y – 2x = 4 in the
xy-plane is part of the graph.
3D Coordinate Systems
The plane y – 2x = 4
y
(0, 4, 0)
(–2, 0, 0)

55. x
z+
Example D. Sketch y – 2x = 4 in R3.
Set x = z = 0  y = 4, we’ve (0, 4, 0),
set y = z = 0  x = –2, we’ve (–2, 0, 0).
We can’t set y = x = 0, so there is no z intercept.
Because the equation doesn't
have the variable z, therefore the
z coordinate assume any value.
Hence all points directly above
and below the line y – 2x = 4
which form a plane parallel to the
x-axis, is the graph.
Plot the x and y intercepts, the line y – 2x = 4 in the
xy-plane is part of the graph.
3D Coordinate Systems
(–2, 0, 0)
(0, 4, 0)
The plane y – 2x = 4
y

56. General Cylinders (Equation with a missing variable)
3D Coordinate Systems

57. General Cylinders (Equation with a missing variable)
3D Coordinate Systems
In general, if an equation has a missing variable then
the missing variable may assume any value.

58. Example E. Sketch z = x2
General Cylinders (Equation with a missing variable)
3D Coordinate Systems
In general, if an equation has a missing variable then
the missing variable may assume any value.

59. Example E. Sketch z = x2
General Cylinders (Equation with a missing variable)
3D Coordinate Systems
In general, if an equation has a missing variable then
the missing variable may assume any value.
To draw the graph of the equation, draw the 2D
curve in the corresponding coordinate plane first,

60. Example E. Sketch z = x2
General Cylinders (Equation with a missing variable)
3D Coordinate Systems
Draw the parabola z = x2 in the xz-plane.
In general, if an equation has a missing variable then
the missing variable may assume any value.
To draw the graph of the equation, draw the 2D
curve in the corresponding coordinate plane first,
z+
x
y

61. Example E. Sketch z = x2
General Cylinders (Equation with a missing variable)
then move the curve in space
parallel to the axis of the missing
variable.
3D Coordinate Systems
Draw the parabola z = x2 in the xz-plane.
In general, if an equation has a missing variable then
the missing variable may assume any value.
To draw the graph of the equation, draw the 2D
curve in the corresponding coordinate plane first,
z+
x
y

62. Example E. Sketch z = x2
General Cylinders (Equation with a missing variable)
then move the curve in space
parallel to the axis of the missing
variable.
3D Coordinate Systems
Draw the parabola z = x2 in the xz-plane. Extending
this parabola in the y (the missing variable) direction
In general, if an equation has a missing variable then
the missing variable may assume any value.
To draw the graph of the equation, draw the 2D
curve in the corresponding coordinate plane first,
z+
x
y

63. Example E. Sketch z = x2
General Cylinders (Equation with a missing variable)
then move the curve in space
parallel to the axis of the missing
variable.
3D Coordinate Systems
Draw the parabola z = x2 in the xz-plane. Extend this
parabola in the y (the missing variable) direction we
get the (parabolic) cylinder-surface as shown.
In general, if an equation has a missing variable then
the missing variable may assume any value.
x
z+
y
To draw the graph of the equation, draw the 2D
curve in the corresponding coordinate plane first,

64. Example E. Sketch z = x2
General Cylinders (Equation with a missing variable)
then move the curve in space
parallel to the axis of the missing
variable. The surface formed is a
general cylinder.
3D Coordinate Systems
Draw the parabola z = x2 in the xz-plane. Extend this
parabola in the y (the missing variable) direction we
get the (parabolic) cylinder-surface as shown.
In general, if an equation has a missing variable then
the missing variable may assume any value.
x
z+
y
To draw the graph of the equation, draw the 2D
curve in the corresponding coordinate plane first,

65. x
z+Equations of Spheres
yThe equation of the sphere with
radius r, centered at (a, b ,c) is
(x – a)2 + (y – b)2 + (z – c)2 = r2.
In particular x2 + y2 + z2 = r2 is the
sphere centered at (0, 0, 0) with
radius r.
(a, b, c)
r
r
(x–a)2+(y–b)2+(z–c)2=r2
x2+y2+z2=r2
3D Coordinate Systems

66. x
z+Equations of Spheres
yThe equation of the sphere with
radius r, centered at (a, b ,c) is
(x – a)2 + (y – b)2 + (z – c)2 = r2.
In particular x2 + y2 + z2 = r2 is the
sphere centered at (0, 0, 0) with
radius r.
(a, b, c)
r
r
(x–a)2+(y–b)2+(z–c)2=r2
x2+y2+z2=r2
Equations of Ellipsoids
The graph of the equation
is the ellipsoid
centered at (a, b ,c), with
x–radius = r, y–radius = s, z–radius = t
(x – a)2 (y – b)2 (z – c)2
r2 s2 t2
= 1++
x
z+
y
(a, b, c)
r
s
t
3D Coordinate Systems

67. The distance D between (x1, y1, z1), (x2, y2, z2) is
Δx2 + Δy2 + Δz2 = (x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2
3D Coordinate Systems
The Distance and the Mid–point Formula in R3

68. The distance D between (x1, y1, z1), (x2, y2, z2) is
Δx2 + Δy2 + Δz2 = (x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2
Hence the distance between (2, –1, 1) and (1, –1, 3),
with Δx = 1, Δy = 0, Δz = –2, is D = 1+ 0 + 4 = 5
3D Coordinate Systems
The Distance and the Mid–point Formula in R3

69. The distance D between (x1, y1, z1), (x2, y2, z2) is
Δx2 + Δy2 + Δz2 = (x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2
Hence the distance between (2, –1, 1) and (1, –1, 3),
with Δx = 1, Δy = 0, Δz = –2, is D = 1+ 0 + 4 = 5
The mid–point of
(x1, y1, z1), (x2, y2, z2) is ( x1+ x2 y1+ y2 z1+ z2
2 2 2, ,
).
3D Coordinate Systems
The Distance and the Mid–point Formula in R3

70. The distance D between (x1, y1, z1), (x2, y2, z2) is
Δx2 + Δy2 + Δz2 = (x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2
Hence the distance between (2, –1, 1) and (1, –1, 3),
with Δx = 1, Δy = 0, Δz = –2, is D = 1+ 0 + 4 = 5
The mid–point of
(x1, y1, z1), (x2, y2, z2) is ( x1+ x2 y1+ y2 z1+ z2
2 2 2, ,
).
3D Coordinate Systems
The Distance and the Mid–point Formula in R3
Example F. Find the equation of the sphere which has
A(2, 1, 3) and B(4, 3, –5) as a diameter.

71. The distance D between (x1, y1, z1), (x2, y2, z2) is
Δx2 + Δy2 + Δz2 = (x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2
Hence the distance between (2, –1, 1) and (1, –1, 3),
with Δx = 1, Δy = 0, Δz = –2, is D = 1+ 0 + 4 = 5
The mid–point of
(x1, y1, z1), (x2, y2, z2) is ( x1+ x2 y1+ y2 z1+ z2
2 2 2, ,
).
3D Coordinate Systems
The Distance and the Mid–point Formula in R3
Example F. Find the equation of the sphere which has
A(2, 1, 3) and B(4, 3, –5) as a diameter.
The center C of the sphere is the mid–point of A and B
so C = (3, 2, –1).

72. The distance D between (x1, y1, z1), (x2, y2, z2) is
Δx2 + Δy2 + Δz2 = (x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2
Hence the distance between (2, –1, 1) and (1, –1, 3),
with Δx = 1, Δy = 0, Δz = –2, is D = 1+ 0 + 4 = 5
The mid–point of
(x1, y1, z1), (x2, y2, z2) is ( x1+ x2 y1+ y2 z1+ z2
2 2 2, ,
).
3D Coordinate Systems
The Distance and the Mid–point Formula in R3
Example F. Find the equation of the sphere which has
A(2, 1, 3) and B(4, 3, –5) as a diameter.
The center C of the sphere is the mid–point of A and B
and C = (3, 2, –1). The radius is the distance from
A to C which is 1 + 1 + 16 = 32.

73. The distance D between (x1, y1, z1), (x2, y2, z2) is
Δx2 + Δy2 + Δz2 = (x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2
Hence the distance between (2, –1, 1) and (1, –1, 3),
with Δx = 1, Δy = 0, Δz = –2, is D = 1+ 0 + 4 = 5
The mid–point of
(x1, y1, z1), (x2, y2, z2) is ( x1+ x2 y1+ y2 z1+ z2
2 2 2, ,
).
3D Coordinate Systems
The Distance and the Mid–point Formula in R3
Example F. Find the equation of the sphere which has
A(2, 1, 3) and B(4, 3, –5) as a diameter.
The center C of the sphere is the mid–point of A and B
and C = (3, 2, –1). The radius is the distance from
A to C which is 1 + 1 + 16 = 32. So the equation is
(x – 3)2 + (y – 2)2 + (z + 1)2 = 18.

74. Cylindrical Coordinates
The cylindrical coordinate system is the combination
of using polar coordinates for points in the xy–plane
with z as the 3rd coordinate.

75. Example G. a. Plot the point (3,120o, 4)
in cylindrical coordinates. Convert it to
rectangular coordinates.
Cylindrical Coordinates
The cylindrical coordinate system is the combination
of using polar coordinates for points in the xy–plane
with z as the 3rd coordinate.

76. Example G. a. Plot the point (3,120o, 4)
in cylindrical coordinate. Convert it to
rectangular coordinate.
3
120o
x
y
z
Cylindrical Coordinates
The cylindrical coordinate system is the combination
of using polar coordinates for points in the xy–plane
with z as the 3rd coordinate.

77. Example G. a. Plot the point (3,120o, 4)
in cylindrical coordinate. Convert it to
rectangular coordinate.
3
120o
4
x
y
z
(3, 120o, 4)
Cylindrical Coordinates
The cylindrical coordinate system is the combination
of using polar coordinates for points in the xy–plane
with z as the 3rd coordinate.

78. Example G. a. Plot the point (3,120o, 4)
in cylindrical coordinate. Convert it to
rectangular coordinate.
3
120o
4
x
y
z
(3, 120o, 4)
x = 3cos(120o) = –3/2
y = 3sin(120o) = 33/2
Hence the point is (–3/2, 33/2, 4)
Cylindrical Coordinates
The cylindrical coordinate system is the combination
of using polar coordinates for points in the xy–plane
with z as the 3rd coordinate.

79. Example G. a. Plot the point (3,120o, 4)
in cylindrical coordinate. Convert it to
rectangular coordinate.
3
120o
4
x
y
z
(3, 120o, 4)
Cylindrical Coordinates
The cylindrical coordinate system is the combination
of using polar coordinates for points in the xy–plane
with z as the 3rd coordinate.
x = 3cos(120o) = –3/2
y = 3sin(120o) = 33/2
Hence the point is (–3/2, 33/2, 4)
b. Convert (3, –3, 1) into
cylindrical coordinates.

80. Example G. a. Plot the point (3,120o, 4)
in cylindrical coordinate. Convert it to
rectangular coordinate.
3
120o
4
x
y
z
(3, 120o, 4)
 = 315o, r = (9 + 9) = 18
Hence the point is (18, 315o, 1)
in cylindrical coordinates.
Cylindrical Coordinates
The cylindrical coordinate system is the combination
of using polar coordinates for points in the xy–plane
with z as the 3rd coordinate.
x = 3cos(120o) = –3/2
y = 3sin(120o) = 33/2
Hence the point is (–3/2, 33/2, 4)
b. Convert (3, –3, 1) into
cylindrical coordinates.

81. Example G. a. Plot the point (3,120o, 4)
in cylindrical coordinate. Convert it to
rectangular coordinate.
3
120o
4
x
y
z
(3, 120o, 4)
(18, 315o, 0)
x
y
Cylindrical Coordinates
z
The cylindrical coordinate system is the combination
of using polar coordinates for points in the xy–plane
with z as the 3rd coordinate.
b. Convert (3, –3, 1) into
cylindrical coordinates.
x = 3cos(120o) = –3/2
y = 3sin(120o) = 33/2
Hence the point is (–3/2, 33/2, 4)
 = 315o, r = (9 + 9) = 18
Hence the point is (18, 315o, 1)
in cylindrical coordinates.

82. Example G. a. Plot the point (3,120o, 4)
in cylindrical coordinate. Convert it to
rectangular coordinate.
3
120o
4
x
y
z
(3, 120o, 4)
(18, 315o, 0)
x
y
Cylindrical Coordinates
z
(18, 315o, 1) = (3, –3, 1)
1
The cylindrical coordinate system is the combination
of using polar coordinates for points in the xy–plane
with z as the 3rd coordinate.
b. Convert (3, –3, 1) into
cylindrical coordinates.
x = 3cos(120o) = –3/2
y = 3sin(120o) = 33/2
Hence the point is (–3/2, 33/2, 4)
 = 315o, r = (9 + 9) = 18
Hence the point is (18, 315o, 1)
in cylindrical coordinates.

83. Cylindrical Coordinates
The constant equations
r = k describe cylinders of
radius k, thus the name
"cylindrical coordinate".

84. The constant equations
r = k describe cylinders of
radius k, thus the name
"cylindrical coordinate".
Example H. a. Sketch r = 2
2
Cylindrical Coordinates
x
y
z

85. The constant equations
r = k describe cylinders of
radius k, thus the name
"cylindrical coordinate".
x
y
Example H. a. Sketch r = 2
2
The constant equations
 = k describe the vertical
planes through the origin,
at the angle k with x-axis.
b. Sketch θ =3π/4
3π/4
Cylindrical Coordinates
z
x
y
z

86. The constant equations
r = k describe cylinders of
radius k, thus the name
"cylindrical coordinate".
x
y
Example H. a. Sketch r = 2
2
The constant equations
 = k describe the vertical
plane through the origin,
at the angle k with x-axis.
b. Sketch θ =3π/4
3π/4
Cylindrical Coordinates
z
x
y
z