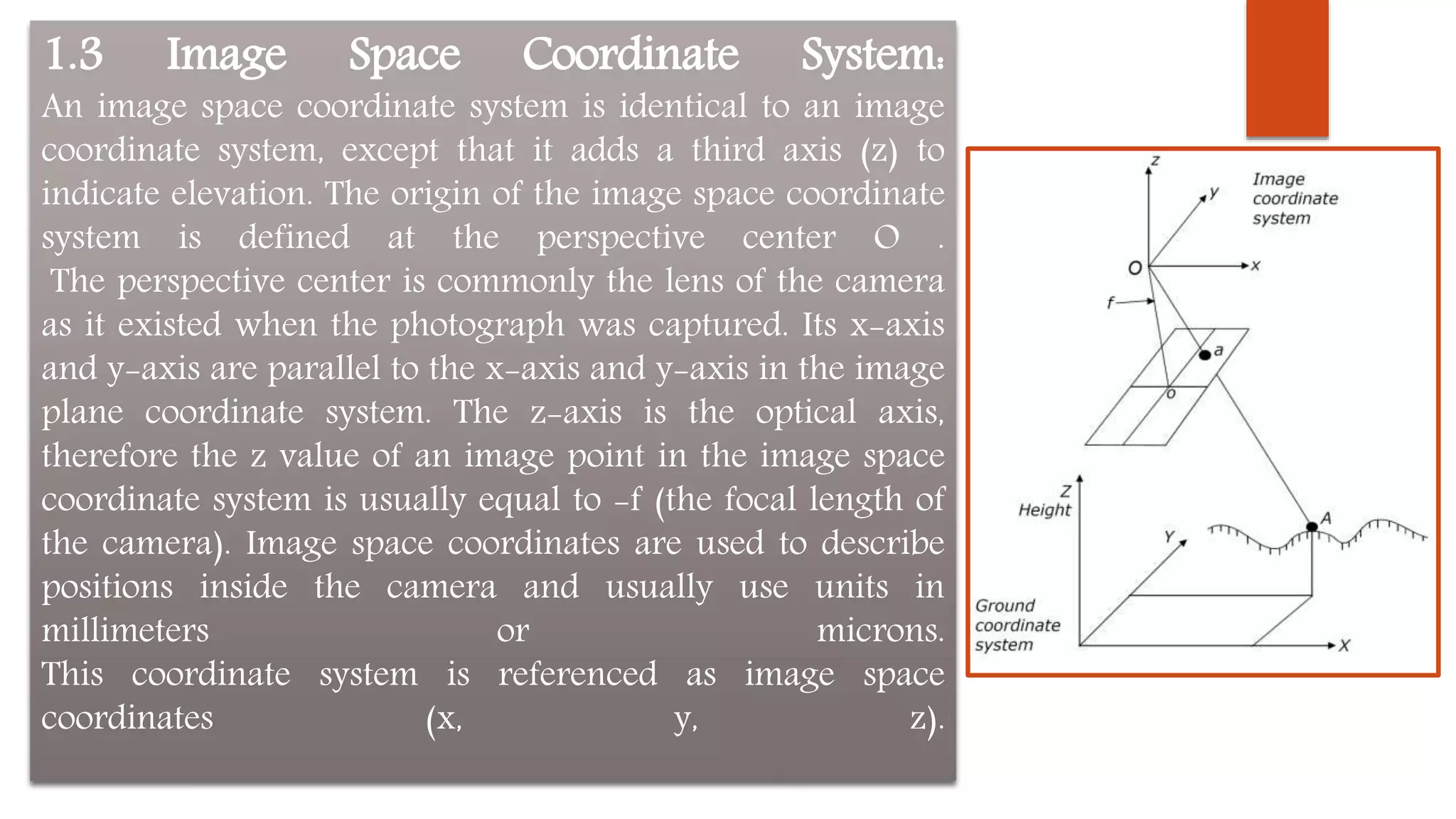
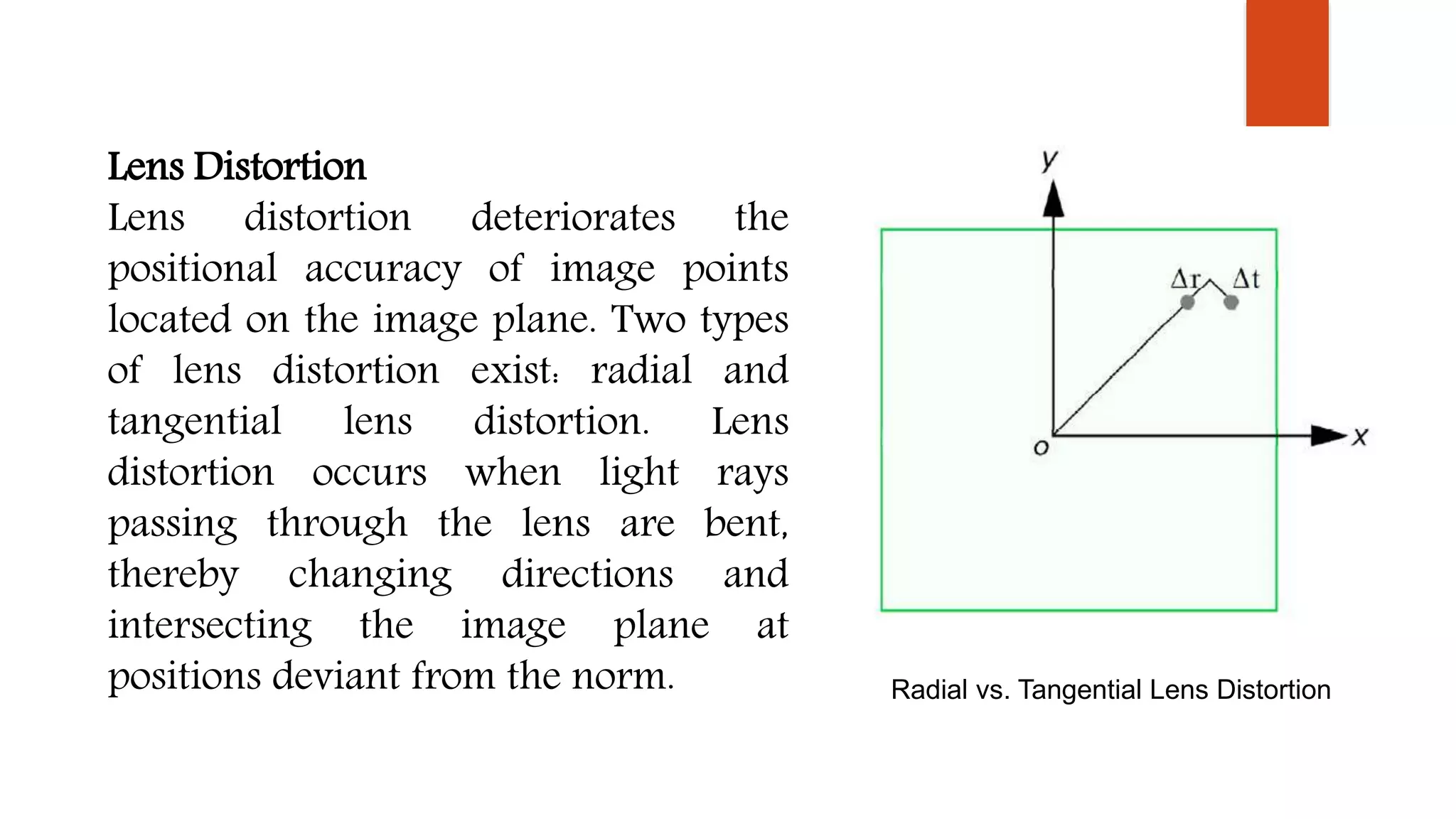
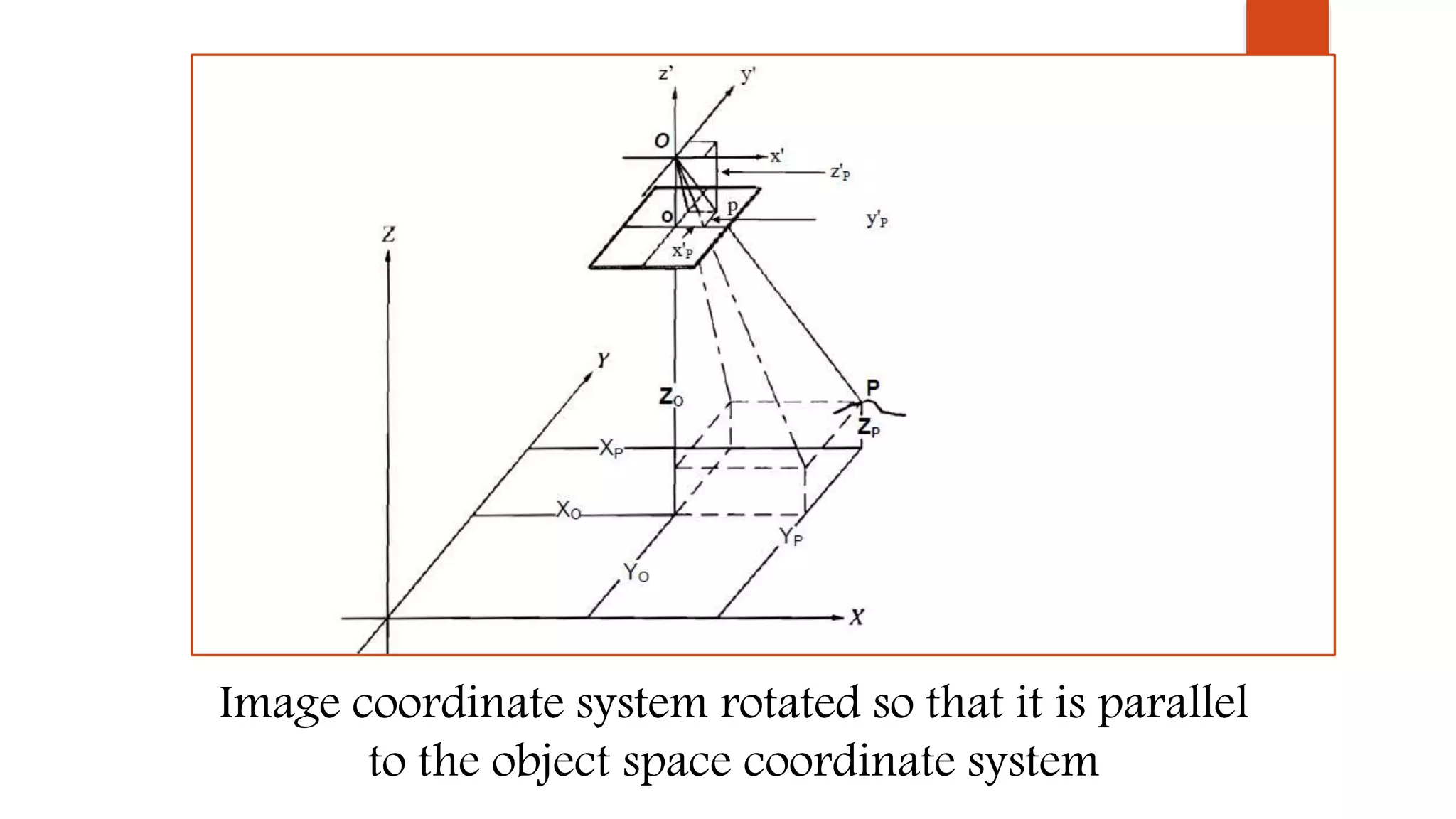
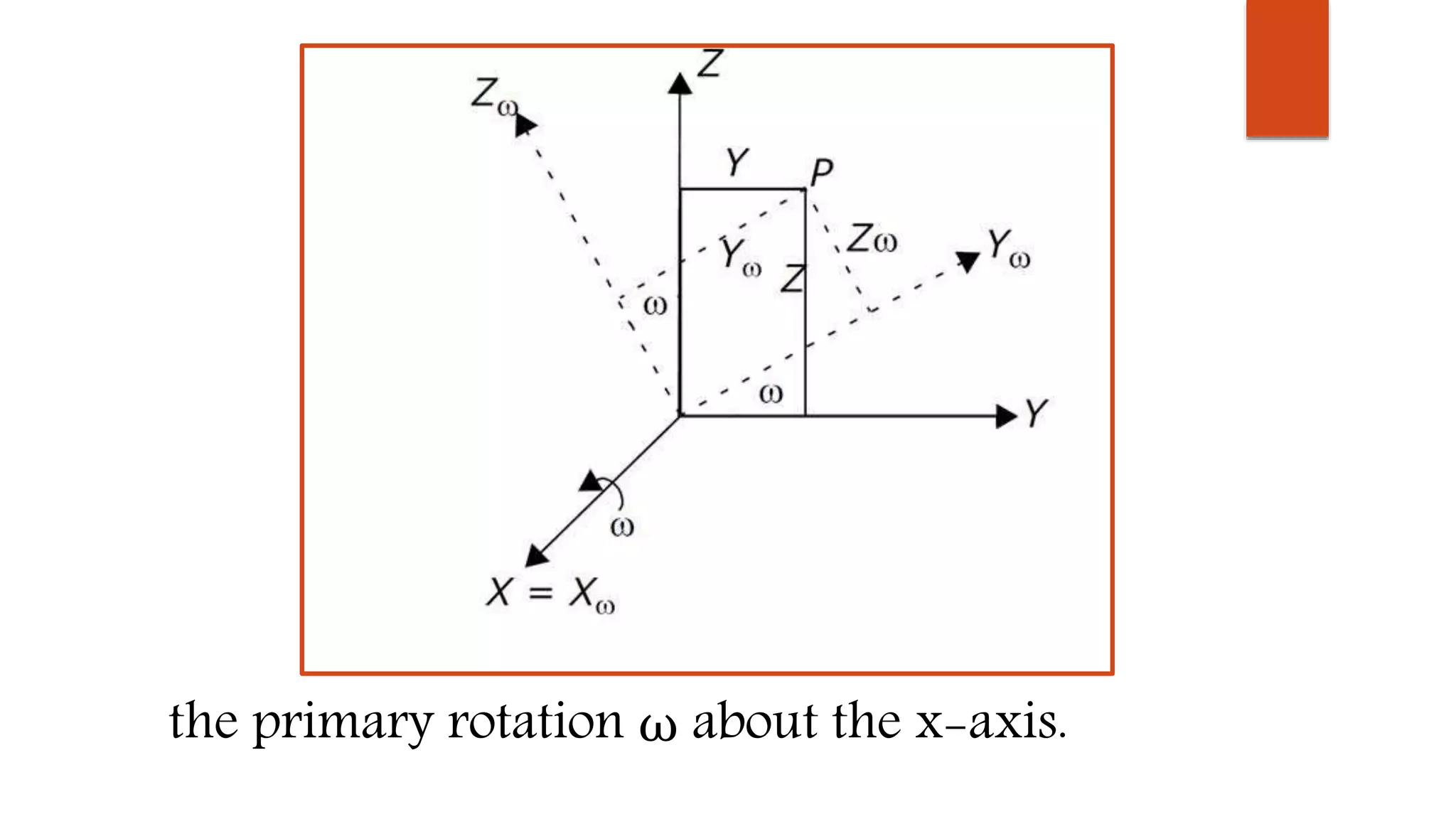
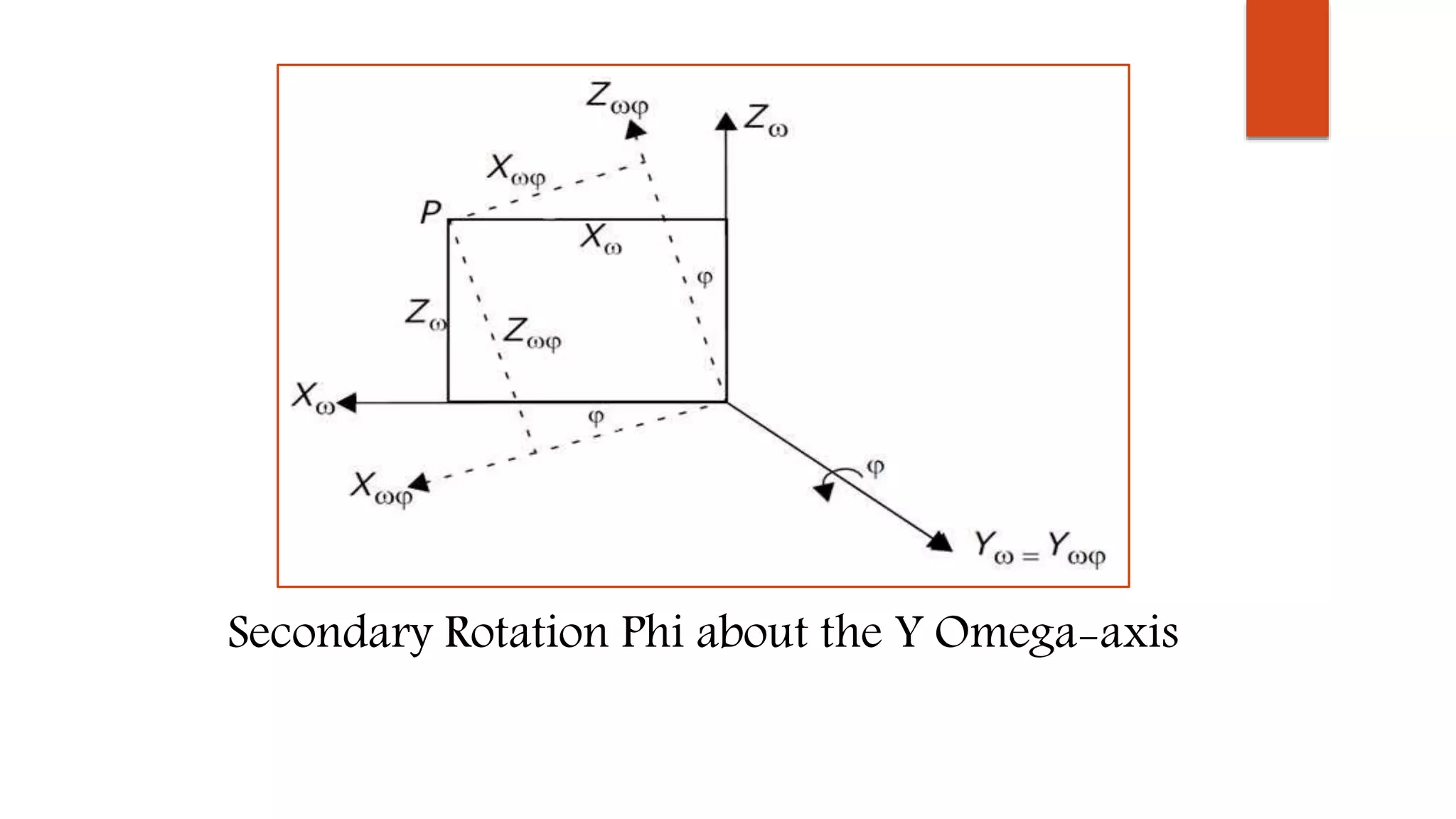
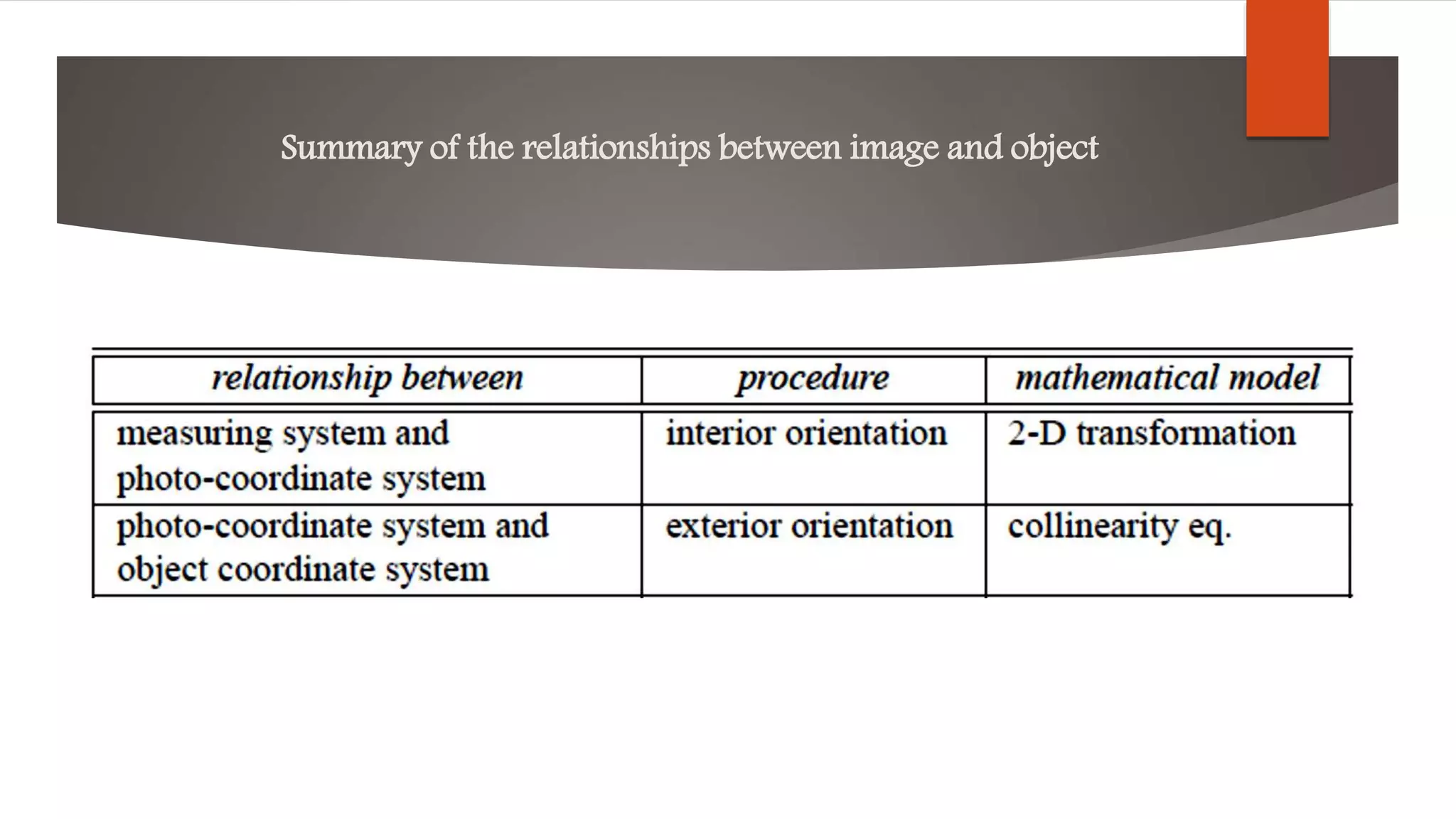
1) The document discusses various coordinate systems used in photogrammetry including pixel, image, image space, and ground coordinate systems. 2) It also covers topics like interior orientation parameters (principal point, focal length), exterior orientation parameters (position and rotation angles), and two-dimensional coordinate transformations. 3) The relationships between the image, camera, and ground coordinates are defined using these parameters and coordinate systems to allow for mapping between the three domains.

1. Elements of Analytical
Photogrammetry

2. content
1. Coordinate Systems.
1.1 Pixel Coordinate System
1.2 Image Coordinate System
1.3 Image Space Coordinate System
1.4 Ground Coordinate System
2. Two dimensional coordinate transformation
2.1 conformal
2.2 affine
3. Interior and Exterior orientation parameters

3. 1. Coordinate Systems
Conceptually, photogrammetry involves establishing the
relationship between the camera or sensor used to capture
the imagery, the imagery itself, and the ground.
In order to understand and define this relationship, each of
the three variables associated with the relationship must be
defined with respect to a coordinate space and coordinate
system.

4. 1.1 Pixel Coordinate System:
pixel coordinate system is usually a
coordinate system with its origin in the
upper-left corner of the image, the x-
axis pointing to the right, the y-axis
pointing downward, and the units in
pixels, as shown by axes c and r .These
coordinates (c, r) can also be thought of
as the pixel column and row number,
respectively.

5. 1.2 Image Coordinate System
An image coordinate system or an image plane coordinate system is usually
defined as a two-dimensional (2D) coordinate system occurring on the image
plane with its origin at the image center. The origin of the image coordinate
system is also referred to as the principal point. Image coordinate units are
usually millimeters or microns.

6. 1.3 Image Space Coordinate System:
An image space coordinate system is identical to an image
coordinate system, except that it adds a third axis (z) to
indicate elevation. The origin of the image space coordinate
system is defined at the perspective center O .
The perspective center is commonly the lens of the camera
as it existed when the photograph was captured. Its x-axis
and y-axis are parallel to the x-axis and y-axis in the image
plane coordinate system. The z-axis is the optical axis,
therefore the z value of an image point in the image space
coordinate system is usually equal to -f (the focal length of
the camera). Image space coordinates are used to describe
positions inside the camera and usually use units in
millimeters or microns.
This coordinate system is referenced as image space
coordinates (x, y, z).

7. A ground coordinate system is usually defined as a 3D
coordinate system that utilizes a known geographic
map projection. Ground coordinates (X,Y,Z) are
usually expressed in feet or meters. The Z value is
elevation above mean sea level for a given vertical
datum. This coordinate system is referenced as ground
coordinates (X,Y,Z).
1.4 Ground Coordinate System

8. 2. Two dimensional coordinate transformation:
2.1 conformal coordinate transformation
The term two-dimensional means that the coordinate systems lie on
plane surfaces. A conformal transformation is one in which true
shape is preserved after transformation. To perform a two-
dimensional conformal coordinate transformation, it is necessary that
coordinates of at least two points be known in both the arbitrary and
final coordinate systems.
Accuracy in the transformation is improved by choosing the two
points as far apart as possible. If more than two control points are
available, an improved solution may be obtained by applying the
method of least squares.

10. b) Rotation between 2D right handed coordinate system.

14. 2.2 Affine Transformation
Two dimensional affine coordinate transformation
The two-dimensional affine coordinate transformation is only a
slight modification of the two-dimensional conformal
transformation, to include different scale factors in the x and y
directions and to compensate for non orthogonality (non
perpendicularity) of the axis system. The affine transformation
achieves these additional features by including two additional
unknown parameters for a total of six. As will be shown, the
derivation of the transformation equations depends on the
measurement characteristics of the arbitrary coordinate system.

16. Summary of Computing Photo-Coordinates
The main steps necessary to determine photo-coordinates:
1. Insert the diapositive into the measuring system (e.g. comparator, analytical
plotter) and measure the fiducial marks in the machine coordinate system.
Compute the transformation parameters with a conformal or affine
transformation. The transformation establishes a relationship between the
measuring system and the fiducial coordinate system.
2. Translate the fiducial system to the photo-coordinate system.
3. Correct photo-coordinates for radial distortion.

17. Interior and Exterior orientation
parameters
 Interior orientation Parameters (IOP)
Interior orientation defines the internal geometry of a camera or sensor as it existed at
the time of image capture. The variables associated with image space are defined during
the process of defining interior orientation. Interior orientation is primarily used to
transform the image pixel coordinate system or other image coordinate measurement
system to the image space coordinate system.

18. Summary of the relationships between image and object

19. Principal Point and Focal Length
The principal point is mathematically defined as the intersection of the
perpendicular line through the perspective center of the image plane.
length from the principal point to the perspective center is called the focal
length.
Fiducial Marks
One of the steps associated with calculating interior orientation involves
determining the image position of the principal point for each image in the
project. Therefore, the image positions of the fiducial marks are measured
on the image, and then compared to the calibrated coordinates of each
fiducial mark.

20. Since the image space coordinate system
has not yet been defined for each image,
the measured image coordinates of the
fiducial marks are referenced to a pixel or
file coordinate system. The pixel
coordinate system has an x coordinate
(column) and a y coordinate (row). The
origin of the pixel coordinate system is the
upper left corner of the image having a
row and column value of 0 and 0,
respectively. Pixel Coordinate System vs. Image Space Coordinate
System

22. Lens Distortion
Lens distortion deteriorates the
positional accuracy of image points
located on the image plane. Two types
of lens distortion exist: radial and
tangential lens distortion. Lens
distortion occurs when light rays
passing through the lens are bent,
thereby changing directions and
intersecting the image plane at
positions deviant from the norm. Radial vs. Tangential Lens Distortion

23. Exterior Orientation Parameters (EOP)
Exterior orientation defines the position and angular orientation of the camera that
captured an image. The variables defining the position and orientation of an image
are referred to as the elements of exterior orientation. The elements of exterior
orientation define the characteristics associated with an image at the time of
exposure or capture. The positional elements of exterior orientation include Xo,
Yo, and Zo. They define the position of the perspective center (O) with respect to
the ground space coordinate system (X, Y, and Z). Zo is commonly referred to as
the height of the camera above sea level, which is commonly defined by a datum.
The angular or rotational elements of exterior orientation describe the relationship
between the ground space coordinate system (X, Y, and Z) and the image space
coordinate system (x, y, and z). Three rotation angles are commonly used to define
angular orientation. They are omega (ω), phi and kappa (κ).

24. Elements of Exterior Orientation

25. Omega, Phi, and Kappa

26. Omega is a rotation about the photographic x-axis, phi is a
rotation about the photographic y-axis, and kappa is a rotation
about the photographic z-axis.
Rotations are defined as being positive if they are
counterclockwise when viewed from the positive end of their
respective axis. The photographic z-axis is equivalent to the
optical axis (focal length). The x’, y’, and z’ coordinates are
parallel to the ground space coordinate system.

27. Using the three rotation angles, the relationship between the image
space coordinate system (x, y, and z) and ground space coordinate
system (X, Y, and Z; or x’, y’, and z’) can be determined. A 3 × 3 matrix
defining the relationship between the two systems is used. This is
referred to as the orientation or rotation matrix, M.
The rotation matrix is derived by applying a sequential rotation of
omega about the x-axis, phi about the y-axis, and kappa about the z-
axis.
Rotation Matrix

28. To derive the rotation matrix M, three rotations are
performed sequentially: a primary rotation ω around the x-
axis, followed by a secondary rotation phi around the y-axis,
and a tertiary rotation κ around the z-axis.
Derivation of the Rotation Matrix

29. the primary rotation ω about the x-axis.

31. Secondary Rotation Phi about the Y Omega-axis

33. Tertiary Rotation Kappa About the Z Omega Phi axis

35. The final effect of all the three rotations is then expressed by
the rotation matrix (M) in which M is the sequential rotation
or orientation matrix. Performing the Multiplication
gives

36. DEVELOPMENT OF COLLINEARITY CONDITION EQUATIONS
Collinearity is the condition in which the exposure station of any
photograph, an object point, and its photo image all lie on a straight
line. The equations expressing this condition are called the collinearity
condition equations. They are perhaps the most useful of all equations
to the photogrammetrist.

38. Image coordinate system rotated so that it is parallel
to the object space coordinate system