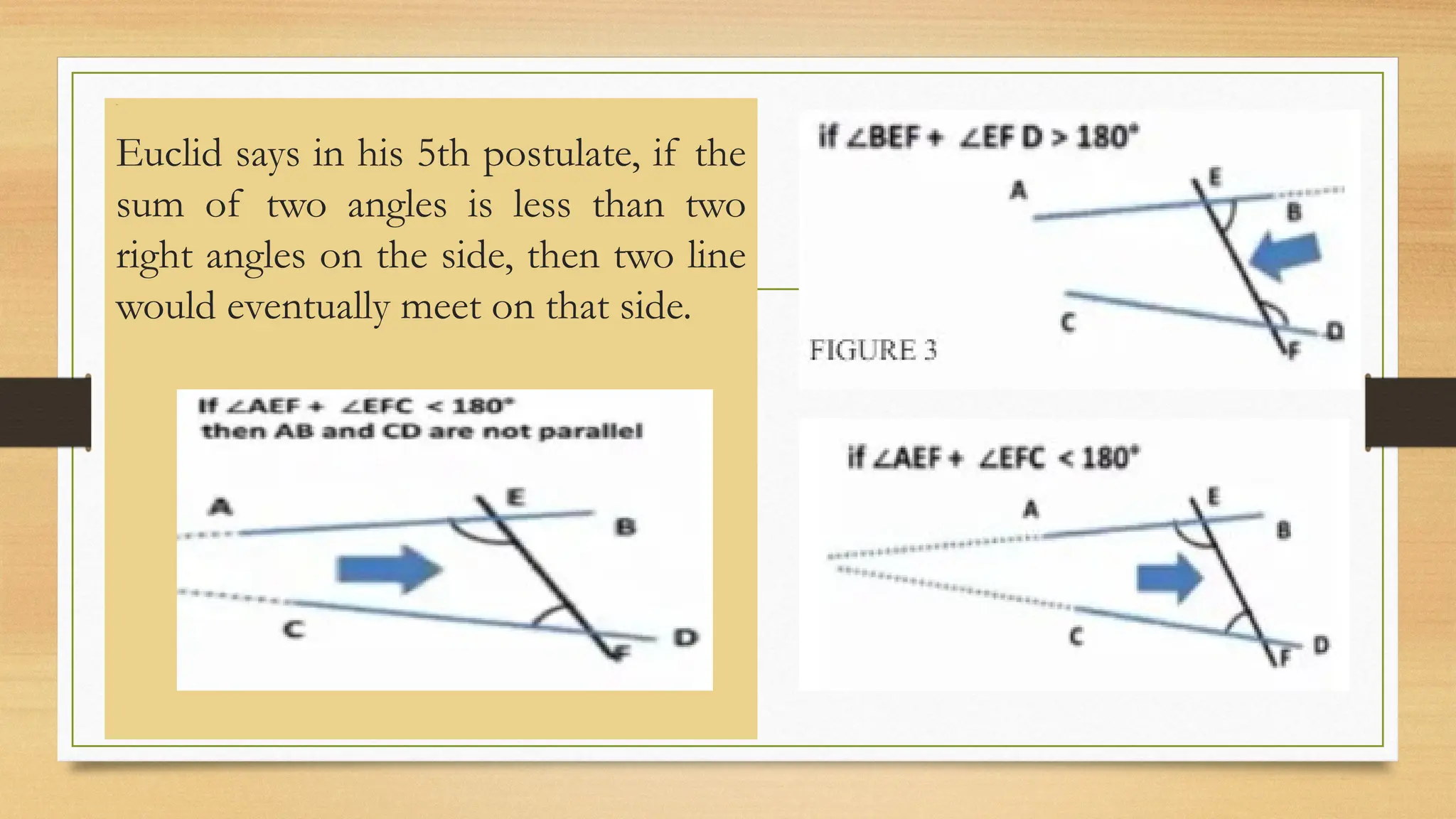
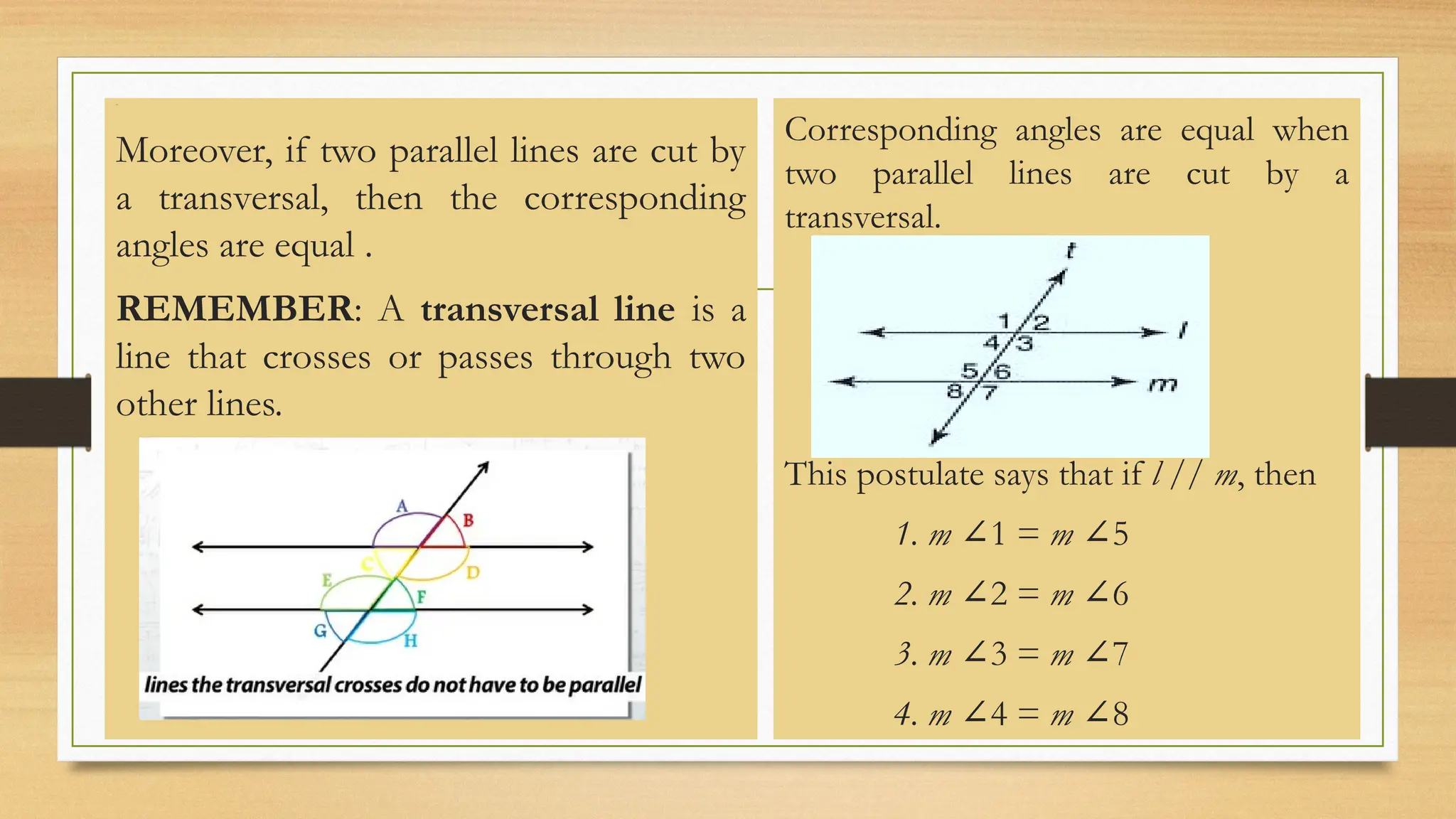
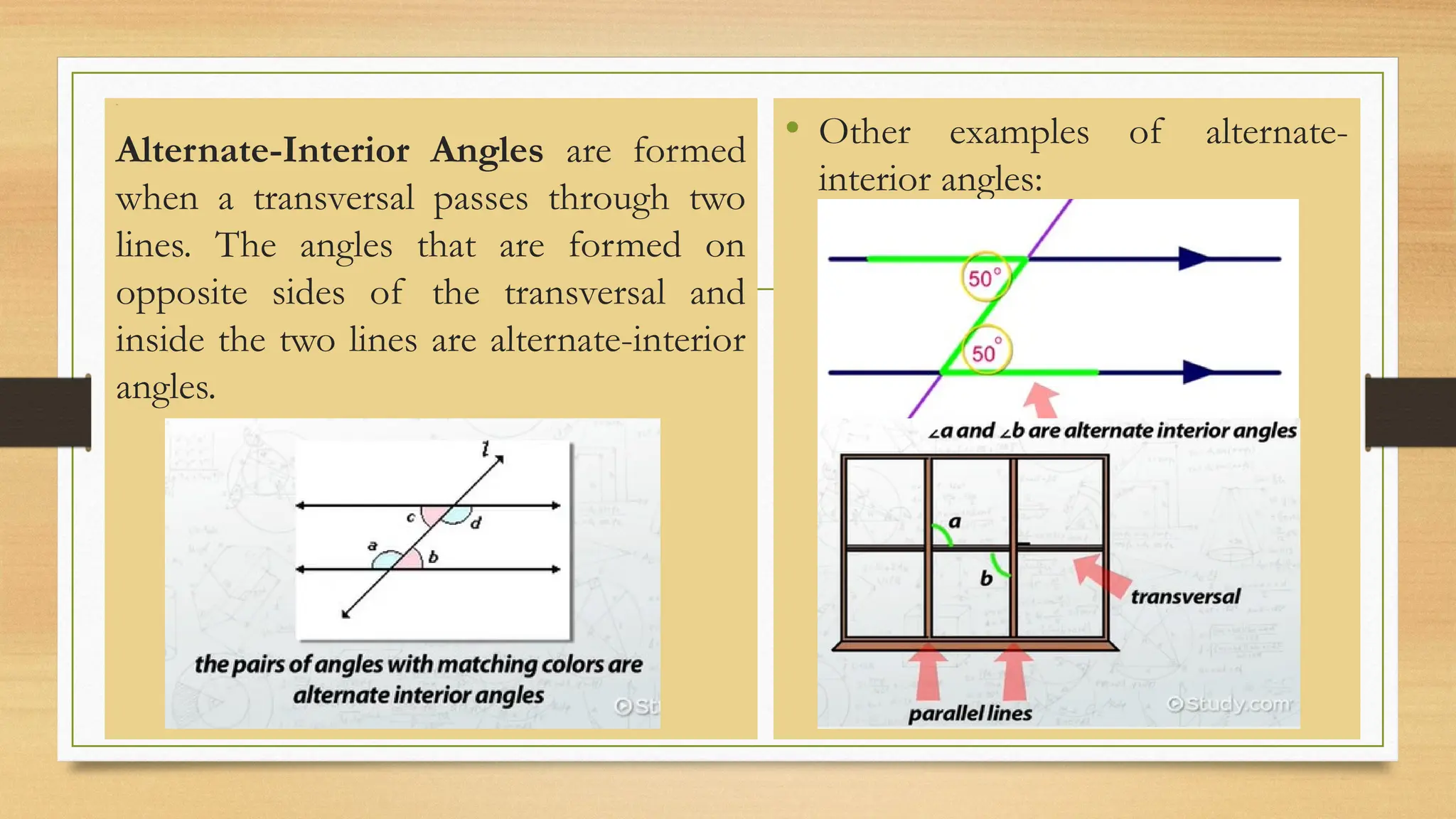
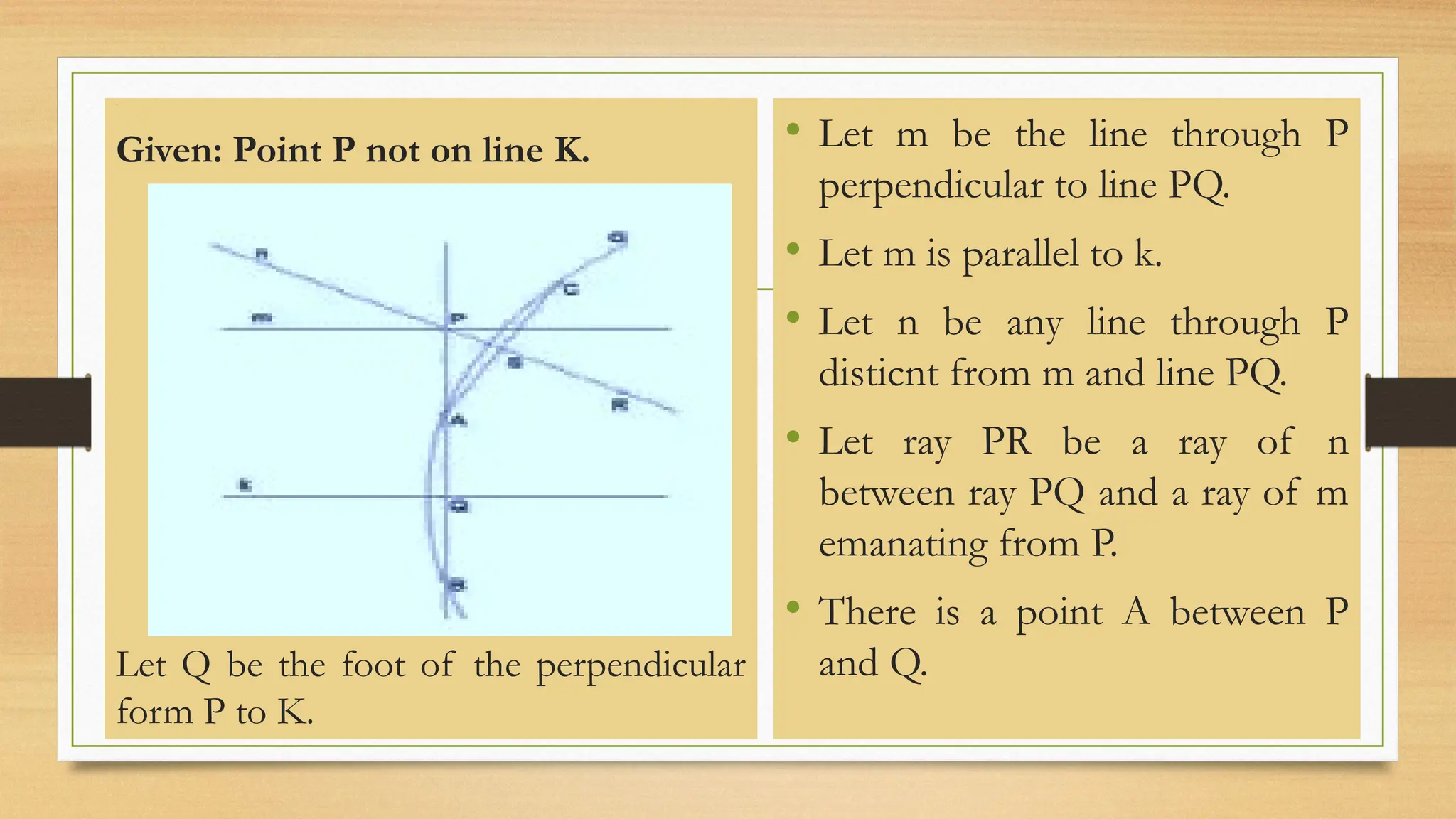
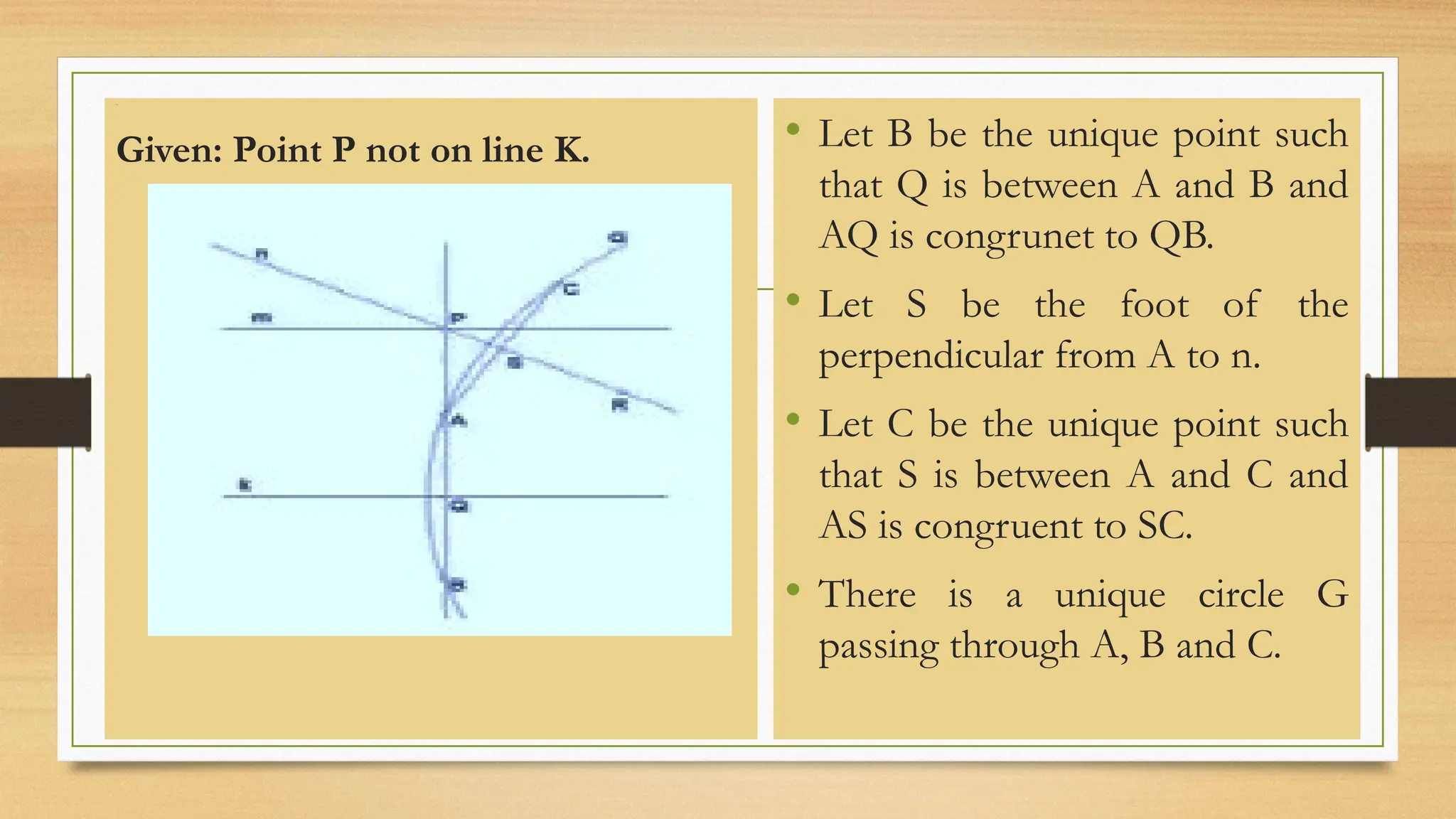
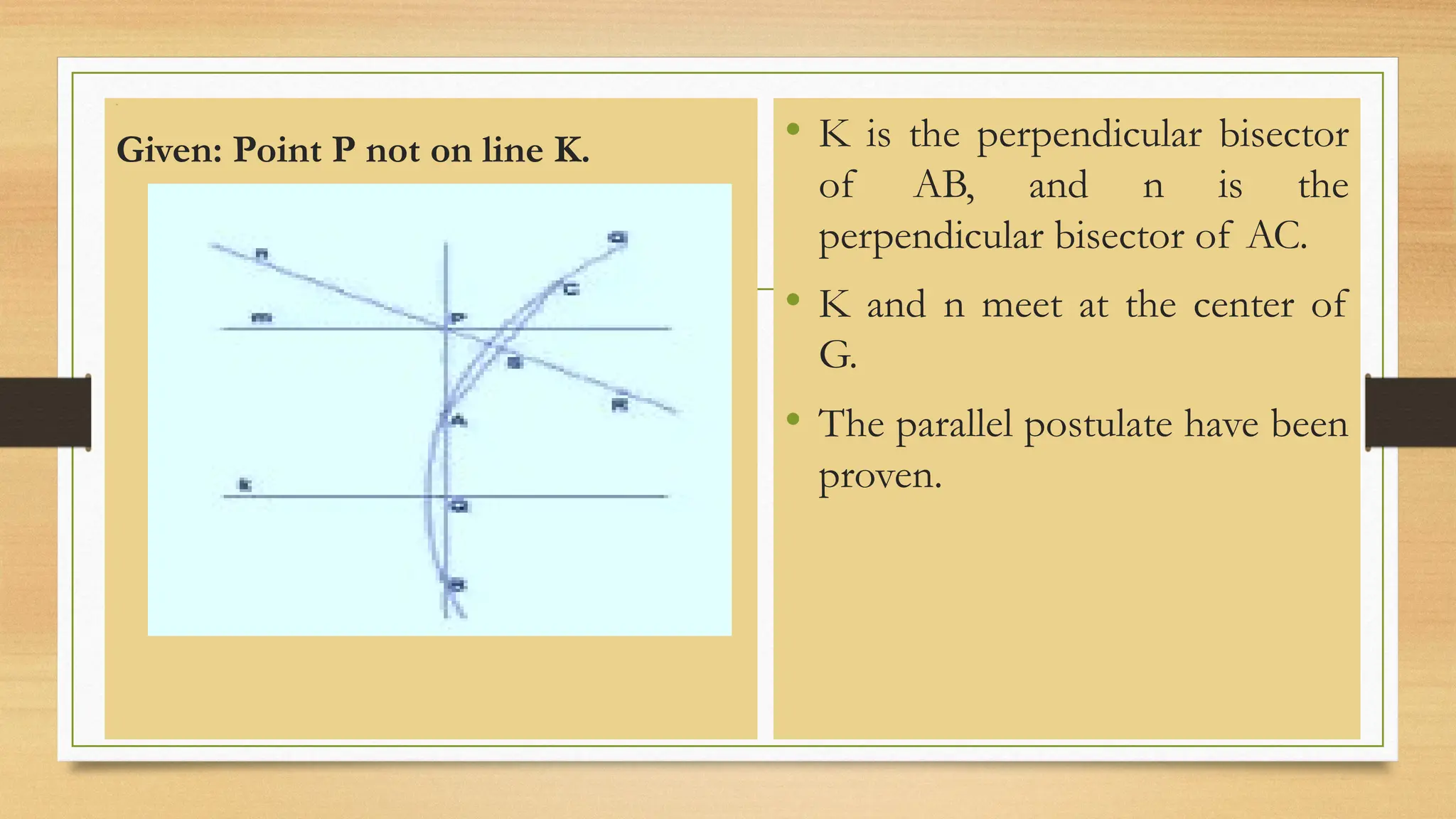
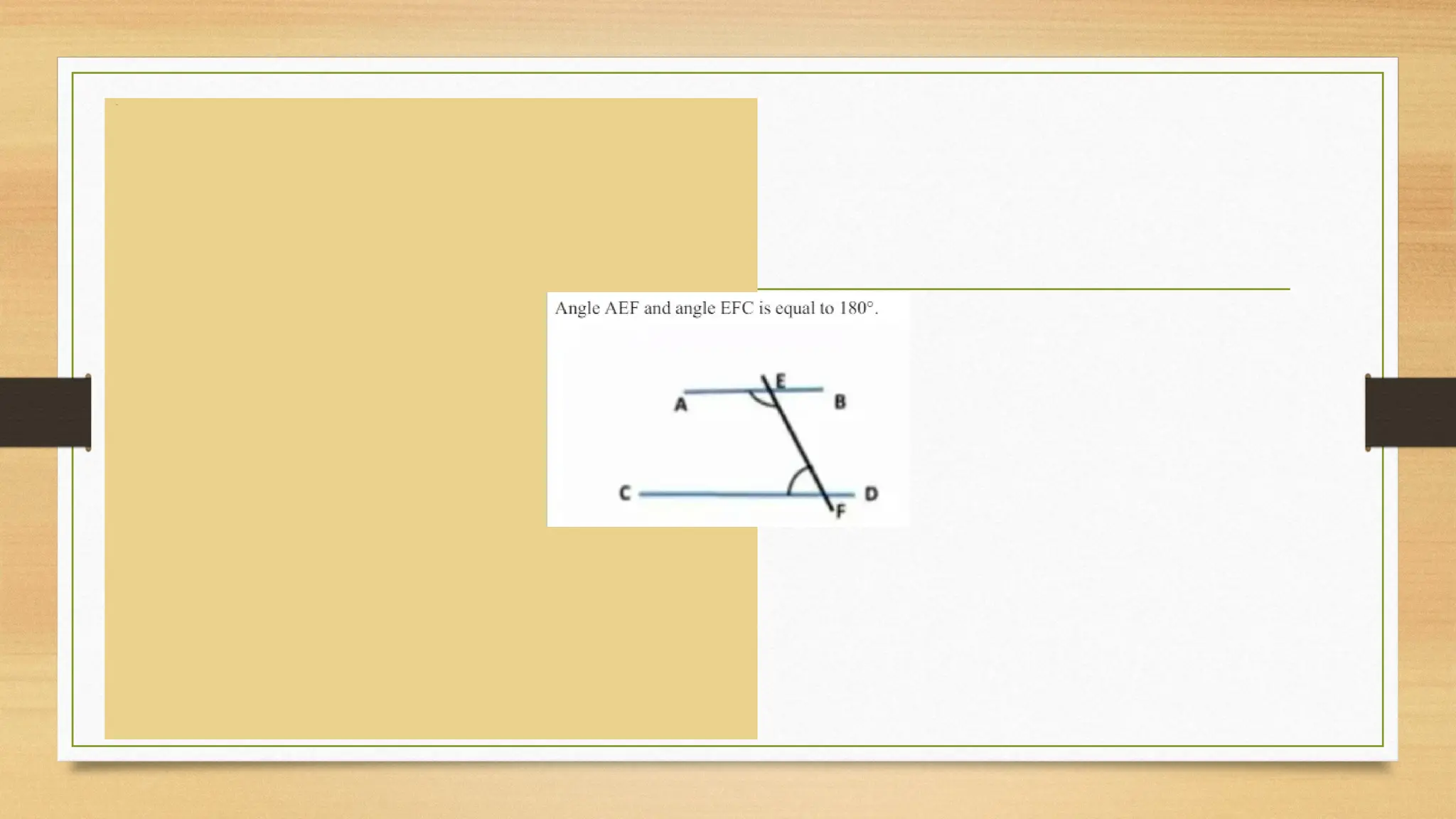
The document provides an overview of classical Euclidean geometry, tracing its origins back to ancient civilizations and key developments by mathematicians such as Euclid. It discusses fundamental concepts in geometry, including undefined terms like points and lines, and Euclid's postulates, particularly the controversial fifth postulate regarding parallel lines. Modern geometry has explored alternatives to this fifth postulate, leading to further advances in the field.

1. MODERN
GEOMETRY
Chapter 1: Classical
Euclidean Geometry

2. OVERVIEW:
The origin of “geometry” comes from the Greek word “geometrein” (geo
means earth and metrein means to measure). Geometry was oiginally the
science of measuring land.
• The study of Geometry is
extremely ancient and has
been carried on for many
thousand of years, across all
civilizations: Egypt,
Babylonian, India, China,
Greece, the Incas, etc.
• Geometry’s origins go back to
approximately 3, 000 BC in ancient
Egypt.
• Ancient Egyptians used an early
form of geometry for a variety of
purposes, including land surbeying,
yramid construction and astronomy.

3. • The Greeks were the first to
establish the concept of proofs in a
systematic way.
• According to the Rhind Papyrus,
the Egyptians in 1800 BC had the
approximation  = 3.1416.
• Egyptian Geometry was not a
science in the Greek sense, but
rather a collection of mathematical
rules with no rationale or
justification.
• In Arithmetic and mathematics,
the Babylonians were far ahead
of the Egyptians. They also
knew the Pythagorean
Theorem.
• Otto Neugebauer;s recent
research has uncovered a
previously undiscovered
Babylonian Algebraic effect on
Greek mathematics.

4. • The Pythagorean Schools systematic
foundation of Plane Geometry was
brought to a concluion by the
mathematician Hippocrates in the
Elements around 400 BC.
• The Pythagoreans were never able to
develop a proprotional theory that
applied to irrational lengths.
• Eudoxus, whose theory was
incorporated into Book V of Euclid’s
Elements, later achieved this
• The next great advance in
geometry was made buy
Eulcid in 30o BC, when he
wrote a book titled
“Elements”
• Euclid’s Elements are a
collection of 13 books that
contain theorems,
constructions, and
geometrical proofs. .

5. • Euclid also prensented an ideal
axiomatic form in this text (now
known as Euclidean Geometry).
• Euclidean geometry is the study of
lines, angles, solid shapes, and
figures using axioms and postulates
to prove propositions using a small
set of statements that are accepted
as true.

6. MODERN
GEOMETRY
Undefined Terms

7. • Undefined terms in geometry refer
to elements that, although often
explained, do not have a formal
definition. These elements serve as
a foundation for other well-defined
elements and theorems. The lack of
a definition of terms
like point and line do not make
them less important or less
concrete.
• Undefined terms are concepts
that are usually described
through examples and visual
representations for not having a
formal description. Some
examples are point, line, plane,
and set. Each of these terms is
of extreme importance for the
construction of theorems and
other concepts.

8. • In Euclidean geometry, undefined
terms, which are arbitrary and could
easily be replaced by other terms,
normally include points, lines and
planes; it would be possible to develop
Euclidean geometry using such
concepts as distance and angle is
undefined. Definitions of new words
involve the use of undefined terms.
• For example, when we say polygon,
we mean that it is a plane figure
bounded by a finite number of a line
segments.
• However, from the definition
itself, we must also define the
other terms used: plane figure
and line segment. If we define a
line segment as a part of a line
that is bounded by two
endpoints. We have to define
again the word line and
endpoints. That’s why we have to
stop somewhere, we have to have
some undefined terms-terms
that do not require definition.

9. • POINT refers to the idea of an
exact, fixed location.
A This is point A
• A point in geometry, can be defined
as a dimensionless mark that
represents a location in space. Its
lack of dimensions refers to the
absence of width, height, and depth
of a point.
• This definition sounds
counterintuitive because a point
is visually presented by a small
circle, which, being a geometric
figure, has two dimensions.
However, one must be aware
that a visual representation
usually brings an extrapolation
of what an element actually is in
theory.

10. • A point indicates a location (or
position) in space.
• A point has no dimension (actual
size)
• A point has no length, no width,
and no height (thickness)
• A point is usually named with a
capital letter.
• In the coordinate plane, a point is
named by an ordered pair, (x, y).
The size of the dot drawn to
represent a point makes no
difference since points have no
size and they simply represent a
location.

11. Line
• LINE is a set of infinite many
points arranged in a straight path
which extends endlessly in opposite
directions. Y
X This is line XY
A Line can also be described as
infinitely long straight mark or band
that goes on forever in both
directions but have no width or
height.
• A Line has no thickness.
• A line’s length extends in one
dimension and goes one forever
in both directions.
• A line has infinite length, zero
width and zero height.
• A Line is assumed to be
straight. (in Euclidean
Geometry)
• A line is drawn with arrowheads
on both ends.

12. Line
• A line is named by a single
lowercase script letter, or by any
two (or more) points which lie on
the line.
This is AB
• The thickness of a line makes no
difference.
• Definition: Collinear points
are points that lie on the same
straight line.
• Postulate: One, and only one,
straight line can be drawn
through two dinstinct points.

13. Line
• PLANE is described as a flat
surface with infinite length and
width, but no thickness.
• A symbol of a plane in Geometry is
usually trapezoid, to appear three-
dimensional and understood to be
infinitely wide and long. A single
capital letter, or three pooints drawn
on it, name the plane.
• A plane is named by a single letter
or by three coplanar, but non-
collinear points.
• While the diagram of a plane has
edges, remember that the plane
actually has no boundaries.
Definition: Coplanar points are
points that lie in the same plane

14. Line
• SET can be described as a
collection of objects, in no
particular order, that you are
studying or mathematically
manipulating.
• Sets can be all these things:
1. Physical objects like angles,
rays, triangles, or circles.
2. Numbers, like all positive even
integers; proper fractions; or
decimals smaller than 0.001
3. Other sets, like set of all
even numbers and the set of
multiples of five; the set of acute
angles and the set of all angles
less than 15.
In geometry, we use sets to group
numbers or items together to
form a single unit, like all the
triangles on a plane or all the
straight angles on a coordinate
grid.

15. MODERN
GEOMETRY
Euclid’s First Four
Postulates

16. Line
Postulate 1: “A straight line can be
drawn from any point to another
point.”
• This postulate states that at least
one straight line passes through two
distinct points but he did not
mention that there cannot be more
than one such line. Although
throughout his work he has
assumed there exists only a unique
line passing through two points.
• This postulate can be extended
to say that a unique (one and
only one) straight line may be
drawn between any two points.

17. Line
Postulate 2: “A terminated line can
be further produced indefinitely.”
• In simple words what we call a line
segment was defined as a
terminated line by Euclid.
Therefore this postulate means that
we can extend a terminated line or a
line segment in either direction to
form a line. In the figure given, the
line segment AB can be extended as
shown to form a line.
• To produce a finite straight line
continuously in a straight line or
a terminated line (a line segmnt)
can be produced indefinitely.

18. Line
Postulate 3: “A circle can be drawn
with any center and any radius.”
• Any circle can be drawn from the
end or start point of a circle and the
diameter of the circle will be the
length of the line segment.
• Given any straight line segment,
a circle, can be drawn having the
segment as radius and one endpoint
as center.
• To describe a circle with any
center and distance.

19. Line
Postulate 4: “All right angles are
equal to one another.”
• All the right angles (i.e. angles
whose measure is 90°) are always
congruent to each other i.e. they are
equal irrespective of their length of
the sides or their orientations.
• Postulate 5: “Given a line L
and a point P not on the line,
exactly one line can be drawn
through P which is parallel to
L.

20. MODERN
GEOMETRY
Parallel Postulate or
Euclid’s 5th Postulate

21. Line
Euclid’s first four postlates have
always been readily accepted by
matehmaticians. The fifth postulate-
the “Parallel Postulate” however,
became highly controversial.
The Fifth Postulate is often called
the Parallel Postulate even though it
does not specifically talk about
parallel lines; it actually deals with the
ideas of parallelism.
• The considerarion of alternatives
to Euclid’s Parallel Postulate
resulted in the development of
non-Euclidean Geometry.

22. Line
Postulate 5: “If a straight line
falling on two straight lines makes
the interior angles on the same side
of it taken together less than two
right angles, then the two straight
lines, if produced indefinitely, meet
on that side on which the sum of
angles is less than two right angles.”
If one line intersects two other
lines, then can you tell whether
these two lines are parallel or not?
• NOTE: If the sum of two
interior angles is 180, then it is
a parallel line.
• In the given diagram, the sum of
angle 1 and angle 2 is less than
180°, so lines n and m will meet
on the side of angle 1 and angle 2.

23. Line
Euclid says in his 5th postulate, if the
sum of two angles is less than two
right angles on the side, then two line
would eventually meet on that side.

24. Line
Moreover, if two parallel lines are cut by
a transversal, then the corresponding
angles are equal .
REMEMBER: A transversal line is a
line that crosses or passes through two
other lines.
Corresponding angles are equal when
two parallel lines are cut by a
transversal.
This postulate says that if l // m, then
1. m 1 =
∠ m 5
∠
2. m 2 =
∠ m 6
∠
3. m 3 =
∠ m 7
∠
4. m 4 =
∠ m 8
∠

25. Line
Alternate-Interior Angles are formed
when a transversal passes through two
lines. The angles that are formed on
opposite sides of the transversal and
inside the two lines are alternate-interior
angles.
• Other examples of alternate-
interior angles:

26. Line
PROPOSITION: “If a straight line
falling on two straight lines make the
alternate angles equal to one another,
the straight lines will be parallel to one
another”
PROOF: Let ST be a transversal
cutting line AB and CD in such a way
that angles BST and CTS are equal
(pabeled a in the figure).
Assume that AB and CD meet in a
point P in the direction of B and D.
Then in triangle SPT, the exterior angle
CTS is equal to the interior opposite
angle TSP. But this is impossible. It
follows that AB and CD cannot meet in
the direction of B and D. By similar
argument, it can be shown that they
cannot meet in the direction of A and
C. Hence they are parallel.

27. Line
PROPOSITION: “If a straight line
falling on two straight lines make the
exterior angle equal to the interior and
opposite angle on the same side, or the
interior angles on the same side equal to
two right angles, the straight lines will
be parallel to one another”
PROOF: Let the straight line EF
falling on the two straight line AB and
CD make the exterior angle EGB equal
to the interior and opposite angle
GHD, or the sum of the interior angle
on the same side, namely BGH and
GHD, equal to two right angles.
AB is parallel to CD. Since the angle
EGB equals the angle GHD and the
angle EGB equals the angle AGH.
Therefore, the angle AGH equals the
angle GHD. And they are alternate.
Therefore, AB is parallel to CD.

28. Line
PROPOSITION: “If a straight line
falling on two straight lines make the
exterior angle equal to the interior and
opposite angle on the same side, or the
interior angles on the same side equal to
two rright angles, the straight lines will
be parallel to one another”
PROOF: Continuation
Next, since the sum of the angles BGH
and GHD equals two right angles and
the sum of the angle AGH and BGH
also equals two right angles, therefore,
the sum of angles AGH and BGH
equals the sum pf the angles NGH
anmd GHD.
Subtract the angle BGH from each.
Therefore, the remaining angle AGH
equals the remaining angle GHD. And
they ae alternate, therefore, AB is
parallel to CD.

29. Line
PROPOSITION: “If a straight line
falling on two straight lines make the
exterior angle equal to the interior and
opposite angle on the same side, or the
interior angles on the same side equal to
two rright angles, the straight lines will
be parallel to one another”
PROOF: Continuation
Therefore, if a straight line falling
on two straight lines makes the
exterior angle equal to the
interiror and opposite angle on
the same side or the sum of the
interior angles on the same side
qual to to right angles, the the
straight line are parallel to one
another.

30. Line
PROPOSITION: “A straight line falling
on parallel straight line make the
alternate angles equal to one another,
the exterior angle equal to the interior
and opposite angle, and the interior
angles on the same side equal to two
right angles.”
PROOF: Let AB and CD be
parallel lines cut in points S and T,
respectively, by the transversal ST.
Assume that angle BST is hreater
than angle CTS. It folloes that the
sam of angles BST and STD is
greater than two right angles and
consequently the sume of angles
AST and CTS is less than two
right angles. Then, by Postulate 5,
AB and CD must meet.

31. Line
PROPOSITION: “A straight line falling
on parallel straight line make the
akternate angles equal to one another,
the exterior angle equal to the interior
and opposite nagle, and the interior
angles on the same side eul to two right
angles.”
PROOF: Continuation
We conclude that angle BST
cannot be greater than angle CTS.
In a simialr way, it can be shown
that angle CTS cannot be greater
than angle BST. The two angles
must be equal and the first part of
the proposition is proved. The
remaining parts are then easily
verified.

32. MODERN
GEOMETRY
Attempts to Prove the
Parallel Postulate

33. Line
Given: Point P not on line K.
Let Q be the foot of the perpendicular
form P to K.
• Let m be the line through P
perpendicular to line PQ.
• Let m is parallel to k.
• Let n be any line through P
disticnt from m and line PQ.
• Let ray PR be a ray of n
between ray PQ and a ray of m
emanating from P.
• There is a point A between P
and Q.

34. Line
Given: Point P not on line K. • Let B be the unique point such
that Q is between A and B and
AQ is congrunet to QB.
• Let S be the foot of the
perpendicular from A to n.
• Let C be the unique point such
that S is between A and C and
AS is congruent to SC.
• There is a unique circle G
passing through A, B and C.

35. Line
Given: Point P not on line K. • K is the perpendicular bisector
of AB, and n is the
perpendicular bisector of AC.
• K and n meet at the center of
G.
• The parallel postulate have been
proven.

36. MODERN
GEOMETRY
Substitutes for Euclid’s
Fifth Postulate

37. Line
Playfair’s Axiom: “Through a given
point, not on a given line, exactly one
line can be drawn parallel to the
given line.”
Playfair’s Axiom is equivalent to the 5th
Postulate in the sense that it can be
deducted from Euclid’s five postulates
and common notios, while conversely,
the 5th Postulate can be deduced from
Playfair;s Axiom together with the
common notions and first tour
postulates.
• The Angle-Sum of a Triangle: “A
second alternative for the 5th
Postulate is the familiar Theorm:
(The sum of the three angles of a
triangle is always equal to two
right angles.)”
• This is a consequence of Playfair’s
Axiom, and hence of the 5th
Postulate, is well known.

38. Line
The Existence of Similar
Figures
The following statement is also
equivaent to the 5th Postulate
and may be susbtituted for it,
leading to the same
consequences:
“There exists a pair of similar
triangles, i.e., triangles which
are not congruent, but have
the three angles of one equal,
respectively, to the three
angles of the other.”
• Equidistant Straight Lines
• Another noteworthy substitute is the following:
• “There exists a pair of straight lines
everywhere equally distant from one
another.”
• Once the 5th Postulate is adopted, this
statement follows, for them all parallels have
this property of being everyhere equally
distant. F the above statement is postulated, we
can easily deduce the 5th Postulate by first
provig that there exists a triangl with the sum
of its angles equal to two right angles.

39. Line