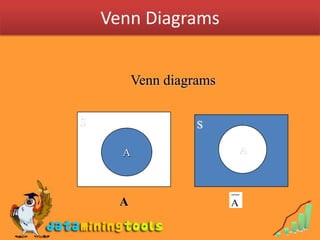
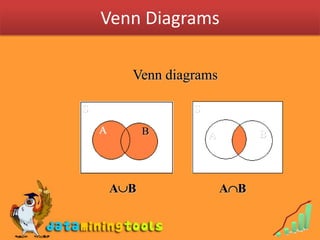
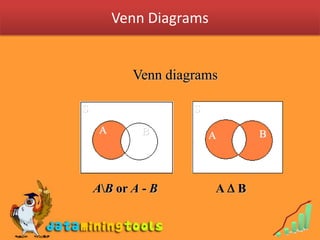
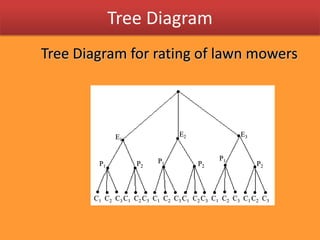
1) A sample space is the set of all possible outcomes of an experiment. Any subset of the sample space is called an event. 2) Events can be mutually exclusive, meaning they cannot occur simultaneously, or not mutually exclusive. 3) Venn diagrams can be used to depict relationships between events, such as intersections and unions. 4) Tree diagrams provide a systematic way to determine the size of a finite sample space when multiple variables are involved.

1. 1.1 Sample Space and events

2. Sample Space and EventsA set of all possible outcomes of an experiment is called a sample space. It is denoted by S.A particular outcome, i.e. an element in S is called a sample point.An experiment consists of the simple process of noting outcomes.The outcome of an experiment may be a simple choice between two alternatives; it may be result of a direct measurement or count; or it may be answer obtained after extensive measurements and calculations.

3. Sample Space and EventsA sample space is said to be discrete if it has finitely many or a countable (denumerable) infinity of elements.If the elements of a sample space constitute a continuum, the sample space is said to be continuous. For example, all points on a line, all points on a line segment, or all points in a plane.Any subset of a sample space is called an event.The subset {a} consisting of a single sample point a  S is called an elementary event. and S itself are subsets of S and so are events.

4. Sample Space and EventsExample 1: A technician has to check the suitability of 3 solid crystal lasers and 2 CO2 lasers for a given task. Let (a,b) represent the event that the technician will find a of the solid crystal lasers and b of the CO2 lasers suitable for the task, then the sample space will be S = {(0,0), (0,1), (0,2), (1,0), (1,1), (1,2), (2,0), (2,1), (2,2), (3,0), (3,1), (3,2)}.

5. Sample Space and EventsR = {(0,0), (1,1), (2,2)} is the event that equally many solid crystal lasers and CO2 lasers are suitable.T = {(0,0), (1,0), (2,0), (3,0)} is the event that none of the CO2 lasers are suitable for the task.U = {(0,1), (0,2), (1,2)} is the event that fewer solid crystal laser than the CO2 lasers are suitable for the task.

6. Sample Space and EventsIf two events have no element in common, they are called mutually exclusive events, i.e. they cannot occur simultaneously.In above example R &T are not mutually exclusive events while R & U and T & U are mutually exclusive events.In order to discuss the basic concepts of the probabilistic model which we wish to develop, it will be very convenient to have available some ideas and concepts of mathematical theory of sets. Sample spaces and events, particularly relationship among events are depicted by means of Venn diagrams

7. Sample Space and EventsIf A and B are any two sets in a sample space S, A B= {x  S | x  A or x  B (or both)}; AB = {x  S | x  A and x  B}; The complement of A i.e. A \ B = A – B = {x  S | x  A and x  B} The symmetric difference of sets A and B i.e. A  B = A \ B  B \ A = A B - AB A set is called empty set and denoted by  which has no elements.

8. Venn DiagramsVenn diagramsSSAAA

9. Venn DiagramsVenn diagramsSSABBAABAB

10. Venn DiagramsVenn diagramsSS ABBAA\B or A - BA  B

11. EventsRU = {(0,0), (1,1), (2,2), (0,1), (0,2), (1,2)} is the event that the number of suitable CO2 lasers is grater than or equal to the number of suitable solid crystal lasers.RT = {(0,0)} is the event that neither CO2 laser nor solid crystal laser is suitable. = {(0,1), (0,2), (1,1), (1,2), (2,1), (2,2), (3,1), (3,2)} is the event that at least one CO2 laser is suitable.

12. At times it can be quite difficult, or at least tedious to determine the number of elements in a finite sample space by direct enumeration.Suppose a consumer testing service, rates lawn mowers a) as being easy, average or difficult to operate; b) as being expensive or inexpensive; and c) as being costly, average or cheap to repair.Events

13. Tree DiagramTo handle this kind of problem systematically we use tree diagram.E1, E2, and E3 denotes three alternatives for ease of operation.P1 and P2 denote two alternatives of price. C1, C2, and C3 denotes three alternatives for cost of repair.

14. Tree DiagramTree Diagram for rating of lawn mowersE2E3E1P1P1P1P2P2P2C2C3C1C1C1C1C1C1C2C2C2C2C2C3C3C3C3C3

15. Tree DiagramFollowing a given path from top to bottom along a branch of the tree, we obtain a particular rating, namely, a particular element of the sample space.This result could also have been obtained by observing that there are three E-branches, that E-branch forks into two P-branches, and that P-branch forks into three C-branches.Thus there are 3.2.3 = 18 combination of branches or paths