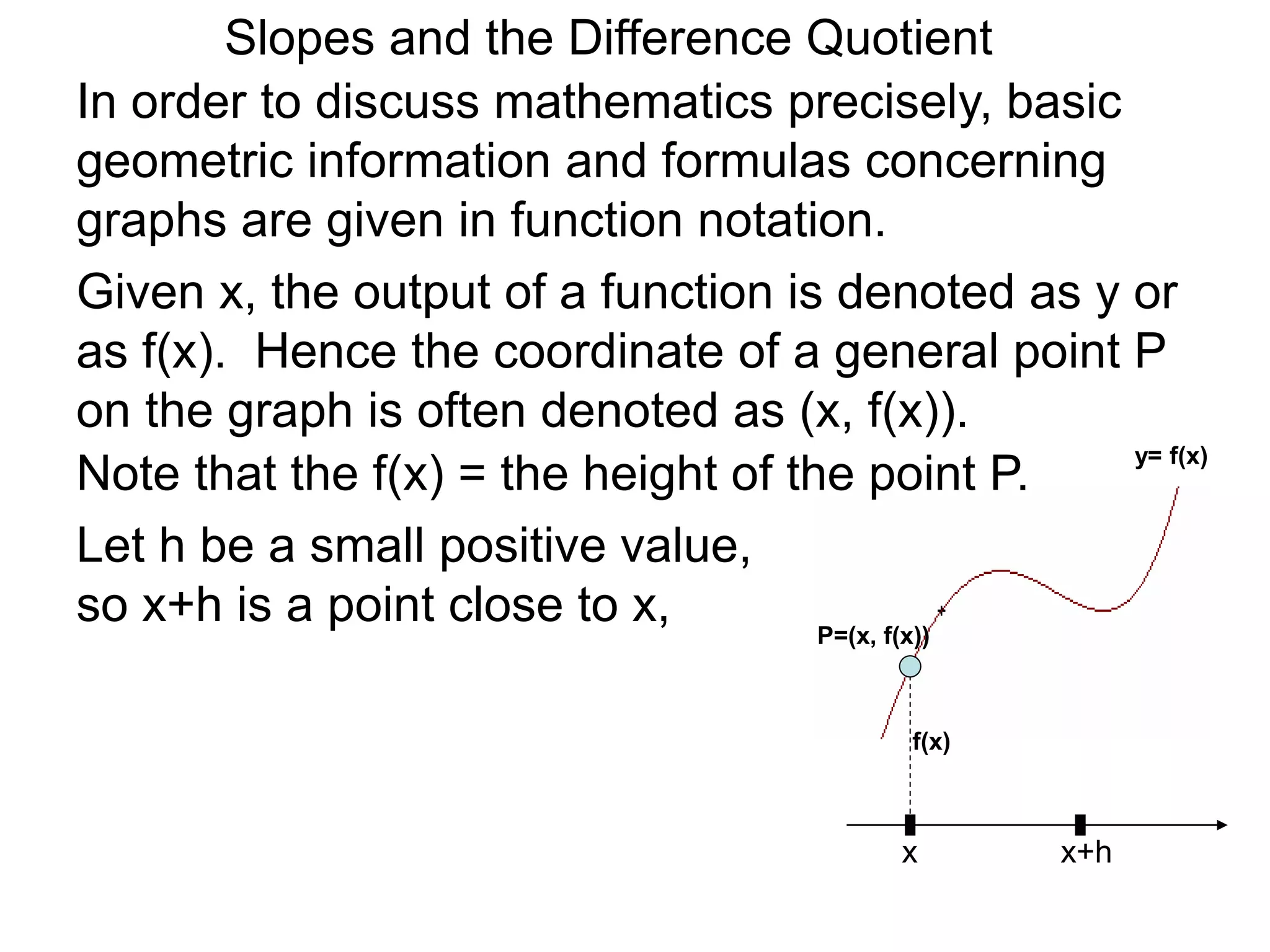
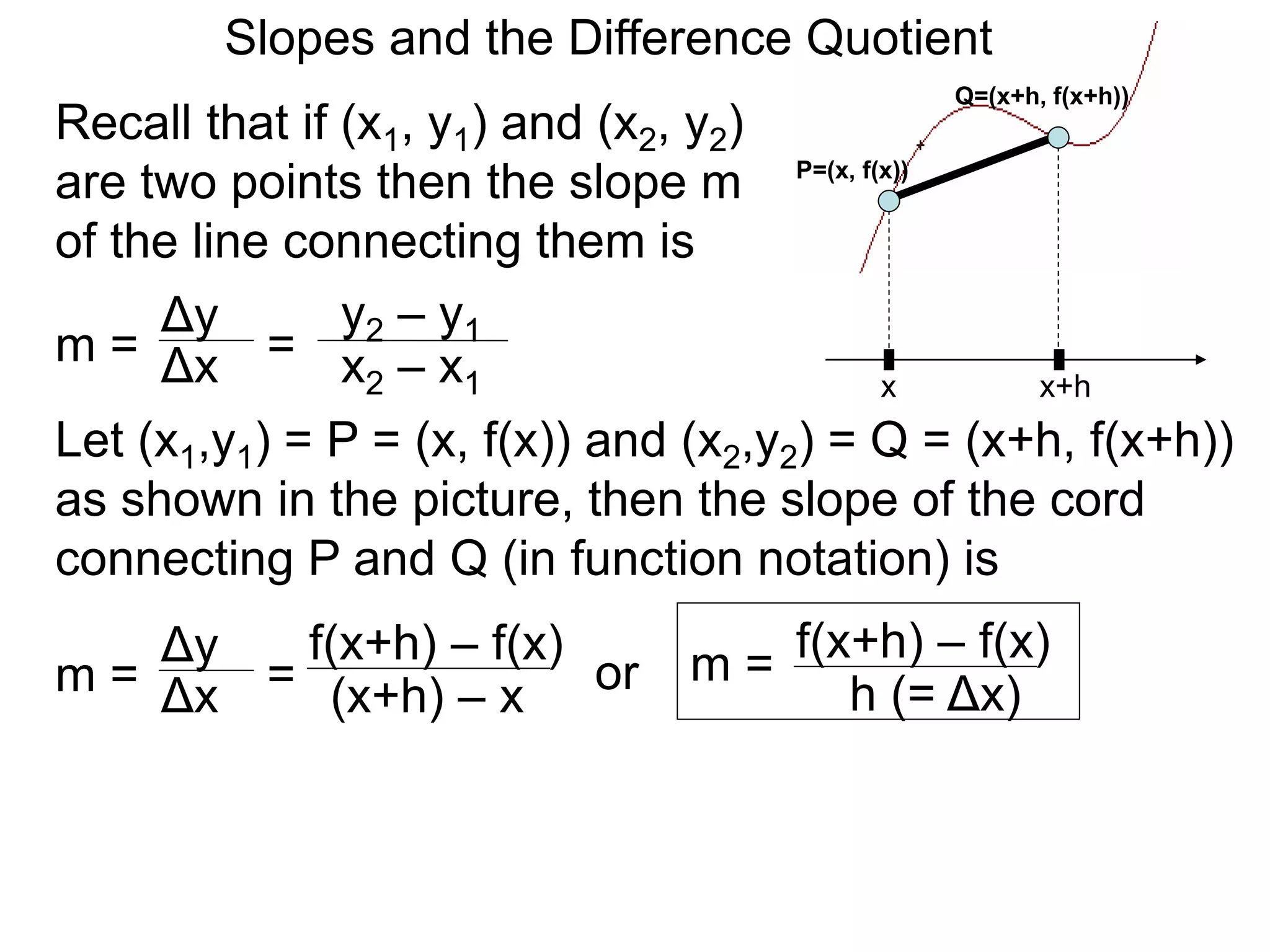
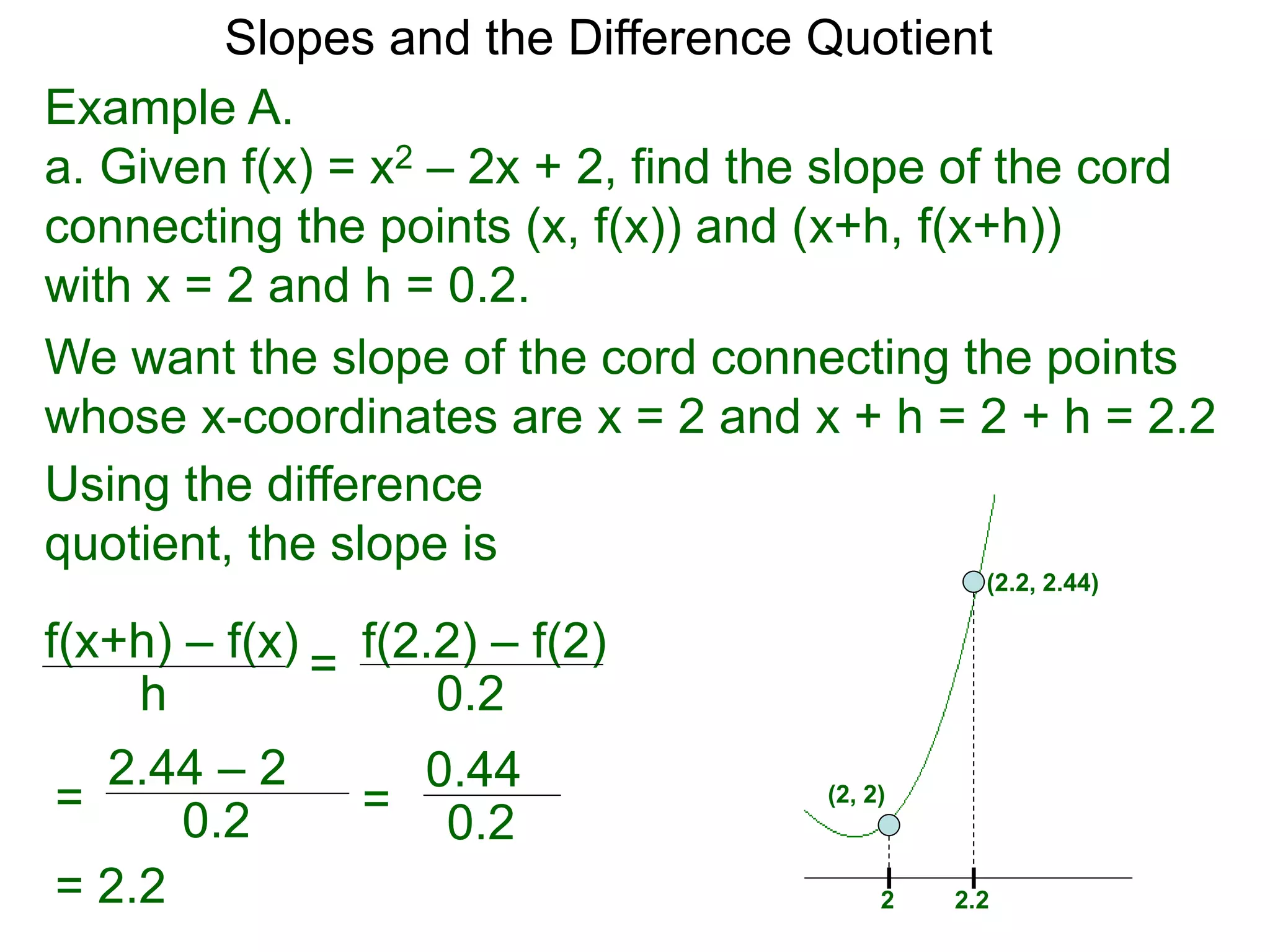
The document discusses calculating the slope of a curve between two points (x, f(x)) and (x+h, f(x+h)) using the difference quotient formula. It defines the difference quotient as (f(x+h) - f(x))/h, where h is the difference between x and x+h. An example calculates the slope between the points (2, f(2)) and (2.2, f(2.2)) for the function f(x) = x^2 - 2x + 2, finding the slope to be 0.44.

1. Slopes and the Difference Quotient
http://www.lahc.edu/math/precalculus/math_260a.html

2. In order to discuss mathematics precisely, basic
geometric information and formulas concerning
graphs are given in function notation.
Slopes and the Difference Quotient

3. Given x, the output of a function is denoted as y or
as f(x).
In order to discuss mathematics precisely, basic
geometric information and formulas concerning
graphs are given in function notation.
Slopes and the Difference Quotient

4. Given x, the output of a function is denoted as y or
as f(x). Hence the coordinate of a general point P
on the graph is often denoted as (x, f(x)).
In order to discuss mathematics precisely, basic
geometric information and formulas concerning
graphs are given in function notation.
Slopes and the Difference Quotient

5. Given x, the output of a function is denoted as y or
as f(x). Hence the coordinate of a general point P
on the graph is often denoted as (x, f(x)).
x
P=(x, f(x))
In order to discuss mathematics precisely, basic
geometric information and formulas concerning
graphs are given in function notation.
y= f(x)
Slopes and the Difference Quotient

6. Given x, the output of a function is denoted as y or
as f(x). Hence the coordinate of a general point P
on the graph is often denoted as (x, f(x)).
In order to discuss mathematics precisely, basic
geometric information and formulas concerning
graphs are given in function notation.
x
P=(x, f(x))
y= f(x)
f(x)
Note that the f(x) = the height of the point P.
Slopes and the Difference Quotient

7. Given x, the output of a function is denoted as y or
as f(x). Hence the coordinate of a general point P
on the graph is often denoted as (x, f(x)).
Let h be a small positive value,
so x+h is a point close to x,
In order to discuss mathematics precisely, basic
geometric information and formulas concerning
graphs are given in function notation.
x
P=(x, f(x))
y= f(x)
f(x)
Note that the f(x) = the height of the point P.
Slopes and the Difference Quotient

8. Given x, the output of a function is denoted as y or
as f(x). Hence the coordinate of a general point P
on the graph is often denoted as (x, f(x)).
x
P=(x, f(x))
Note that the f(x) = the height of the point P.
Let h be a small positive value,
so x+h is a point close to x,
x+h
In order to discuss mathematics precisely, basic
geometric information and formulas concerning
graphs are given in function notation.
f(x)
y= f(x)
Slopes and the Difference Quotient

9. Given x, the output of a function is denoted as y or
as f(x). Hence the coordinate of a general point P
on the graph is often denoted as (x, f(x)).
x
P=(x, f(x))
Note that the f(x) = the height of the point P.
Let h be a small positive value,
so x+h is a point close to x,
x+h
then f(x+h) is the output for x+h,
and (x+h, f(x+h)) represents the
corresponding point, say Q,
on the graph.
In order to discuss mathematics precisely, basic
geometric information and formulas concerning
graphs are given in function notation.
f(x)
y= f(x)
Slopes and the Difference Quotient

10. Given x, the output of a function is denoted as y or
as f(x). Hence the coordinate of a general point P
on the graph is often denoted as (x, f(x)).
x
P=(x, f(x))
Note that the f(x) = the height of the point P.
Let h be a small positive value,
so x+h is a point close to x,
x+h
then f(x+h) is the output for x+h,
and (x+h, f(x+h)) represents the
corresponding point, say Q,
on the graph.
In order to discuss mathematics precisely, basic
geometric information and formulas concerning
graphs are given in function notation.
Q=(x+h, f(x+h))
f(x)
y= f(x)
Slopes and the Difference Quotient

11. Given x, the output of a function is denoted as y or
as f(x). Hence the coordinate of a general point P
on the graph is often denoted as (x, f(x)).
x
P=(x, f(x))
Note that the f(x) = the height of the point P.
Let h be a small positive value,
so x+h is a point close to x,
x+h
then f(x+h) is the output for x+h,
and (x+h, f(x+h)) represents the
corresponding point, say Q,
on the graph.
In order to discuss mathematics precisely, basic
geometric information and formulas concerning
graphs are given in function notation.
Note that the f(x+h) = the height of the point Q.
Q=(x+h, f(x+h))
f(x)
f(x+h)
y= f(x)
Slopes and the Difference Quotient

12. Recall that if (x1, y1) and (x2, y2)
are two points then the slope m
of the line connecting them is
Δy
m =
y2 – y1
= x2 – x1
Δx
Slopes and the Difference Quotient

13. Recall that if (x1, y1) and (x2, y2)
are two points then the slope m
of the line connecting them is
Δy
m =
y2 – y1
= x2 – x1
Δx
Let (x1,y1) = P = (x, f(x)) and (x2,y2) = Q = (x+h, f(x+h))
as shown in the picture,
Slopes and the Difference Quotient

14. Recall that if (x1, y1) and (x2, y2)
are two points then the slope m
of the line connecting them is
x
P=(x, f(x))
x+h
Q=(x+h, f(x+h))
Δy
m =
y2 – y1
= x2 – x1
Δx
Let (x1,y1) = P = (x, f(x)) and (x2,y2) = Q = (x+h, f(x+h))
as shown in the picture,
Slopes and the Difference Quotient

15. Recall that if (x1, y1) and (x2, y2)
are two points then the slope m
of the line connecting them is
x
P=(x, f(x))
x+h
Q=(x+h, f(x+h))
Δy
m =
y2 – y1
= x2 – x1
Δx
Let (x1,y1) = P = (x, f(x)) and (x2,y2) = Q = (x+h, f(x+h))
as shown in the picture, then the slope of the cord
connecting P and Q (in function notation) is
Slopes and the Difference Quotient

16. Recall that if (x1, y1) and (x2, y2)
are two points then the slope m
of the line connecting them is
x
P=(x, f(x))
x+h
Q=(x+h, f(x+h))
Δy
m =
y2 – y1
= x2 – x1
Δx
Let (x1,y1) = P = (x, f(x)) and (x2,y2) = Q = (x+h, f(x+h))
as shown in the picture, then the slope of the cord
connecting P and Q (in function notation) is
Δy
m =
f(x+h) – f(x)
= (x+h) – x
Δx
Slopes and the Difference Quotient

17. Recall that if (x1, y1) and (x2, y2)
are two points then the slope m
of the line connecting them is
x
P=(x, f(x))
x+h
Q=(x+h, f(x+h))
Δy
m =
y2 – y1
= x2 – x1
Δx
Let (x1,y1) = P = (x, f(x)) and (x2,y2) = Q = (x+h, f(x+h))
as shown in the picture, then the slope of the cord
connecting P and Q (in function notation) is
Δy
m =
f(x+h) – f(x)
= (x+h) – x
Δx or
Slopes and the Difference Quotient
m = f(x+h) – f(x)
h (= Δx)

18. Recall that if (x1, y1) and (x2, y2)
are two points then the slope m
of the line connecting them is
x
P=(x, f(x))
x+h
Q=(x+h, f(x+h))
Δy
m =
y2 – y1
= x2 – x1
Δx
Let (x1,y1) = P = (x, f(x)) and (x2,y2) = Q = (x+h, f(x+h))
as shown in the picture, then the slope of the cord
connecting P and Q (in function notation) is
Δy
m =
f(x+h) – f(x)
= (x+h) – x
Δx or
This is the "difference quotient" formula for slopes
Slopes and the Difference Quotient
m = f(x+h) – f(x)
h (= Δx)

19. Recall that if (x1, y1) and (x2, y2)
are two points then the slope m
of the line connecting them is
x
P=(x, f(x))
x+h
Q=(x+h, f(x+h))
Δy
m =
y2 – y1
= x2 – x1
Δx
Let (x1,y1) = P = (x, f(x)) and (x2,y2) = Q = (x+h, f(x+h))
as shown in the picture, then the slope of the cord
connecting P and Q (in function notation) is
Δy
m =
f(x+h) – f(x)
= (x+h) – x
Δx or m = f(x+h) – f(x)
h (= Δx)
f(x+h)–f(x) = Δy
because f(x+h) – f(x) = difference in height
This is the "difference quotient" formula for slopes
Slopes and the Difference Quotient

20. Recall that if (x1, y1) and (x2, y2)
are two points then the slope m
of the line connecting them is
x
P=(x, f(x))
x+h
Q=(x+h, f(x+h))
Δy
m =
y2 – y1
= x2 – x1
Δx
Let (x1,y1) = P = (x, f(x)) and (x2,y2) = Q = (x+h, f(x+h))
as shown in the picture, then the slope of the cord
connecting P and Q (in function notation) is
Δy
m =
f(x+h) – f(x)
= (x+h) – x
Δx or
h=Δx
f(x+h)–f(x) = Δy
because f(x+h) – f(x) = difference in height and
h = (x+h) – x = Δx = difference in the x's, as shown.
This is the "difference quotient" formula for slopes.
Slopes and the Difference Quotient
m = f(x+h) – f(x)
h (= Δx)

21. Example A.
a. Given f(x) = x2 – 2x + 2, find the slope of the cord
connecting the points (x, f(x)) and (x+h, f(x+h))
with x = 2 and h = 0.2.
Slopes and the Difference Quotient

22. Example A.
a. Given f(x) = x2 – 2x + 2, find the slope of the cord
connecting the points (x, f(x)) and (x+h, f(x+h))
with x = 2 and h = 0.2.
We want the slope of the cord connecting the points
whose x-coordinates are x = 2 and x + h = 2 + h = 2.2.
Slopes and the Difference Quotient

23. Example A.
a. Given f(x) = x2 – 2x + 2, find the slope of the cord
connecting the points (x, f(x)) and (x+h, f(x+h))
with x = 2 and h = 0.2.
f(x+h) – f(x)
h
Using the difference
quotient, the slope is
We want the slope of the cord connecting the points
whose x-coordinates are x = 2 and x + h = 2 + h = 2.2
Slopes and the Difference Quotient

24. Example A.
a. Given f(x) = x2 – 2x + 2, find the slope of the cord
connecting the points (x, f(x)) and (x+h, f(x+h))
with x = 2 and h = 0.2.
f(x+h) – f(x)
h
Using the difference
quotient, the slope is
We want the slope of the cord connecting the points
whose x-coordinates are x = 2 and x + h = 2 + h = 2.2
f(2.2) – f(2)
=
Slopes and the Difference Quotient

25. Example A.
a. Given f(x) = x2 – 2x + 2, find the slope of the cord
connecting the points (x, f(x)) and (x+h, f(x+h))
with x = 2 and h = 0.2.
f(x+h) – f(x)
h
Using the difference
quotient, the slope is
We want the slope of the cord connecting the points
whose x-coordinates are x = 2 and x + h = 2 + h = 2.2
f(2.2) – f(2)
0.2
=
Slopes and the Difference Quotient

26. Example A.
a. Given f(x) = x2 – 2x + 2, find the slope of the cord
connecting the points (x, f(x)) and (x+h, f(x+h))
with x = 2 and h = 0.2.
f(x+h) – f(x)
h
Using the difference
quotient, the slope is
We want the slope of the cord connecting the points
whose x-coordinates are x = 2 and x + h = 2 + h = 2.2
f(2.2) – f(2)
0.2
=
=
2.44 – 2
0.2
Slopes and the Difference Quotient

27. Example A.
a. Given f(x) = x2 – 2x + 2, find the slope of the cord
connecting the points (x, f(x)) and (x+h, f(x+h))
with x = 2 and h = 0.2.
f(x+h) – f(x)
h
Using the difference
quotient, the slope is
We want the slope of the cord connecting the points
whose x-coordinates are x = 2 and x + h = 2 + h = 2.2
f(2.2) – f(2)
0.2
=
=
2.44 – 2
0.2 =
0.44
0.2
Slopes and the Difference Quotient

28. Example A.
a. Given f(x) = x2 – 2x + 2, find the slope of the cord
connecting the points (x, f(x)) and (x+h, f(x+h))
with x = 2 and h = 0.2.
f(x+h) – f(x)
h
Using the difference
quotient, the slope is
We want the slope of the cord connecting the points
whose x-coordinates are x = 2 and x + h = 2 + h = 2.2
f(2.2) – f(2)
0.2
=
=
2.44 – 2
0.2
= 2.2
=
0.44
0.2
Slopes and the Difference Quotient

29. Example A.
a. Given f(x) = x2 – 2x + 2, find the slope of the cord
connecting the points (x, f(x)) and (x+h, f(x+h))
with x = 2 and h = 0.2.
f(x+h) – f(x)
h
Using the difference
quotient, the slope is
We want the slope of the cord connecting the points
whose x-coordinates are x = 2 and x + h = 2 + h = 2.2
f(2.2) – f(2)
0.2
=
=
2.44 – 2
0.2
= 2.2
(2.2, 2.44)
(2, 2)
2 2.2
=
0.44
0.2
Slopes and the Difference Quotient

30. Example A.
a. Given f(x) = x2 – 2x + 2, find the slope of the cord
connecting the points (x, f(x)) and (x+h, f(x+h))
with x = 2 and h = 0.2.
f(x+h) – f(x)
h
Using the difference
quotient, the slope is
We want the slope of the cord connecting the points
whose x-coordinates are x = 2 and x + h = 2 + h = 2.2
f(2.2) – f(2)
0.2
=
=
2.44 – 2
0.2
= 2.2
(2.2, 2.44)
(2, 2)
2 2.2
=
0.44
0.2
0.44
0.2
slope m = 2.2
Slopes and the Difference Quotient

31. The algebra of calculating the slopes of some basic
types of functions are given below.
Slope Algebra

32. The algebra of calculating the slopes of some basic
types of functions are given below.
Slope Algebra
Example B. Simplify the difference quotient.
Make sure the h is cancelled.
a. (2nd degree polynomials) f(x) = –2x2 + 3x + 1

33. The algebra of calculating the slopes of some basic
types of functions are given below.
Slope Algebra
Example B. Simplify the difference quotient.
Make sure the h is cancelled.
f(x+h) – f(x)
h
=
a. (2nd degree polynomials) f(x) = –2x2 + 3x + 1

34. The algebra of calculating the slopes of some basic
types of functions are given below.
Slope Algebra
Example B. Simplify the difference quotient.
Make sure the h is cancelled.
f(x+h) – f(x)
h
=
–2(x+h)2 + 3(x+h) + 1 – [–2x2 +3x +1]
h
a. (2nd degree polynomials) f(x) = –2x2 + 3x + 1

35. The algebra of calculating the slopes of some basic
types of functions are given below.
Slope Algebra
Example B. Simplify the difference quotient.
Make sure the h is cancelled.
f(x+h) – f(x)
h
=
–2(x+h)2 + 3(x+h) + 1 – [–2x2 +3x +1]
h
a. (2nd degree polynomials) f(x) = –2x2 + 3x + 1
–2x2 –4xh –2h2 +3x +3h +1 – [–2x2 +3x +1]
h
=

36. The algebra of calculating the slopes of some basic
types of functions are given below.
Slope Algebra
Example B. Simplify the difference quotient.
Make sure the h is cancelled.
f(x+h) – f(x)
h
=
–2(x+h)2 + 3(x+h) + 1 – [–2x2 +3x +1]
h
a. (2nd degree polynomials) f(x) = –2x2 + 3x + 1
–2x2 –4xh –2h2 +3x +3h +1 – [–2x2 +3x +1]
h
=
–4xh –2h2 +3h
h
=
h(–4x –2h +3)
h
=

37. The algebra of calculating the slopes of some basic
types of functions are given below.
Slope Algebra
Example B. Simplify the difference quotient.
Make sure the h is cancelled.
f(x+h) – f(x)
h
=
–2(x+h)2 + 3(x+h) + 1 – [–2x2 +3x +1]
h
a. (2nd degree polynomials) f(x) = –2x2 + 3x + 1
–2x2 –4xh –2h2 +3x +3h +1 – [–2x2 +3x +1]
h
=
–4xh –2h2 +3h
h
=
h(–4x –2h +3)
h
= = –4x –2h +3

38. Rational Expressions
b. (Simple rational function) f(x) = x – 1
2

39. Rational Expressions
b. (Simple rational function) f(x) = x – 1
2
Simplify the difference quotient.

40. Rational Expressions
–
x + h – 1
2
x – 1
2
h
b. (Simple rational function) f(x) = x – 1
2
Simplify the difference quotient.
f(x+h) – f(x)
h =

41. Rational Expressions
–
x + h – 1
2
x – 1
2
h
Multiply the top and bottom by (x + h – 1)(x – 1)
to remove fractions in the numerator.
b. (Simple rational function) f(x) = x – 1
2
Simplify the difference quotient.
f(x+h) – f(x)
h =

42. Rational Expressions
–
x + h – 1
2
x – 1
2
h
Multiply the top and bottom by (x + h – 1)(x – 1)
to remove fractions in the numerator.
b. (Simple rational function) f(x) = x – 1
2
Simplify the difference quotient.
f(x+h) – f(x)
h =
–
x + h – 1
2
x – 1
2
h
[ ]

43. Rational Expressions
–
x + h – 1
2
x – 1
2
h
Multiply the top and bottom by (x + h – 1)(x – 1)
to remove fractions in the numerator.
(x + h –1)(x – 1)
(x + h –1)(x – 1)
*
b. (Simple rational function) f(x) = x – 1
2
Simplify the difference quotient.
f(x+h) – f(x)
h =
–
x + h – 1
2
x – 1
2
h
[ ]

44. Rational Expressions
–
x + h – 1
2
x – 1
2
h
Multiply the top and bottom by (x + h – 1)(x – 1)
to remove fractions in the numerator.
(x + h –1)(x – 1)
(x + h –1)(x – 1)
*
=
–
2(x – 1) 2(x + h –1)
h
b. (Simple rational function) f(x) = x – 1
2
Simplify the difference quotient.
f(x+h) – f(x)
h =
–
x + h – 1
2
x – 1
2
h
(x + h –1)(x – 1)
[ ]

45. Rational Expressions
–
x + h – 1
2
x – 1
2
h
Multiply the top and bottom by (x + h – 1)(x – 1)
to remove fractions in the numerator.
(x + h –1)(x – 1)
(x + h –1)(x – 1)
*
=
–
2(x – 1) 2(x + h –1)
h
b. (Simple rational function) f(x) = x – 1
2
Simplify the difference quotient.
f(x+h) – f(x)
h =
–
x + h – 1
2
x – 1
2
h
(x + h –1)(x – 1) =
– 2h
h(x + h –1)(x – 1)
[ ]

46. Rational Expressions
–
x + h – 1
2
x – 1
2
h
Multiply the top and bottom by (x + h – 1)(x – 1)
to remove fractions in the numerator.
(x + h –1)(x – 1)
(x + h –1)(x – 1)
*
=
–
2(x – 1) 2(x + h –1)
h
b. (Simple rational function) f(x) = x – 1
2
Simplify the difference quotient.
f(x+h) – f(x)
h =
–
x + h – 1
2
x – 1
2
h
(x + h –1)(x – 1) =
– 2h
h(x + h –1)(x – 1)
=
–2
(x + h –1)(x – 1)
[ ]

47. Rational Expressions
c. (Simple root function) f(x) = √2x – 3
Simplify the difference quotient.
f(x+h) – f(x)
h

48. Rational Expressions
h
c. (Simple root function) f(x) = √2x – 3
Simplify the difference quotient.
f(x+h) – f(x)
h =
√2(x + h) – 3 – √2x – 3

49. Rational Expressions
h
c. (Simple root function) f(x) = √2x – 3
Simplify the difference quotient.
f(x+h) – f(x)
h =
√2(x + h) – 3 – √2x – 3
Rationalize the numerator to cancel the h in the
denominator so we may take the limits.
h
√2x + 2h – 3 – √2x – 3
*
√2x + 2h – 3 +√2x – 3
√2x + 2h – 3 +√2x – 3

50. Rational Expressions
h
c. (Simple root function) f(x) = √2x – 3
Simplify the difference quotient.
f(x+h) – f(x)
h =
√2(x + h) – 3 – √2x – 3
Rationalize the numerator to cancel the h in the
denominator so we may take the limits.
h
√2x + 2h – 3 – √2x – 3
*
=
√2x + 2h – 3 +√2x – 3
√2x + 2h – 3 +√2x – 3
2x + 2h – 3 – (2x – 3)
h √2x – 3
√2x + h – 3 +
1
*

51. Rational Expressions
h
c. (Simple root function) f(x) = √2x – 3
Simplify the difference quotient.
f(x+h) – f(x)
h =
√2(x + h) – 3 – √2x – 3
Rationalize the numerator to cancel the h in the
denominator so we may take the limits.
h
√2x + 2h – 3 – √2x – 3
*
=
√2x + 2h – 3 +√2x – 3
√2x + 2h – 3 +√2x – 3
2x + 2h – 3 – (2x – 3)
h √2x – 3
√2x + h – 3 +
1
= 2h
h √2x – 3
√2x + h – 3 +
1
*
*

52. Rational Expressions
h
c. (Simple root function) f(x) = √2x – 3
Simplify the difference quotient.
f(x+h) – f(x)
h =
√2(x + h) – 3 – √2x – 3
Rationalize the numerator to cancel the h in the
denominator so we may take the limits.
h
√2x + 2h – 3 – √2x – 3
*
=
√2x + 2h – 3 +√2x – 3
√2x + 2h – 3 +√2x – 3
2x + 2h – 3 – (2x – 3)
h √2x – 3
√2x + h – 3 +
1
= 2h
h √2x – 3
√2x + h – 3 +
1
=
√2x – 3
√2x + h – 3 +
2
*
*

53. Another version of the difference
quotient formula is to use points
P = (a, f(a)) and Q= (b, f(b)). We get
a
P=(a, f(a))
b
Q=(b, f(b))
Δy
m =
f(b) – f(a)
= b – a
Δx
b-a=Δx
f(b)–f(a) = Δy
Slopes and the Difference Quotient

54. Example B.
a. Given f(x) = x2 – 2x + 2, find the slope of the cord
connecting the points (a, f(a)) and (b,f(b)) with a = 3
and b = 5.
Slopes and the Difference Quotient

55. Example B.
a. Given f(x) = x2 – 2x + 2, find the slope of the cord
connecting the points (a, f(a)) and (b,f(b)) with a = 3
and b = 5.
We want the slope of the cord connecting the points
whose x-coordinates are a = 3 and b = 5
Slopes and the Difference Quotient

56. Example B.
a. Given f(x) = x2 – 2x + 2, find the slope of the cord
connecting the points (a, f(a)) and (b,f(b)) with a = 3
and b = 5.
f(b) – f(a)
b – a
Using the formula, the slope is
We want the slope of the cord connecting the points
whose x-coordinates are a = 3 and b = 5
Slopes and the Difference Quotient

57. Example B.
a. Given f(x) = x2 – 2x + 2, find the slope of the cord
connecting the points (a, f(a)) and (b,f(b)) with a = 3
and b = 5.
f(b) – f(a)
b – a
Using the formula, the slope is
We want the slope of the cord connecting the points
whose x-coordinates are a = 3 and b = 5
f(5) – f(3)
5 – 3
=
Slopes and the Difference Quotient

58. Example B.
a. Given f(x) = x2 – 2x + 2, find the slope of the cord
connecting the points (a, f(a)) and (b,f(b)) with a = 3
and b = 5.
f(b) – f(a)
b – a
Using the formula, the slope is
We want the slope of the cord connecting the points
whose x-coordinates are a = 3 and b = 5
f(5) – f(3)
5 – 3
=
=
17 – 5
2
Slopes and the Difference Quotient

59. Example B.
a. Given f(x) = x2 – 2x + 2, find the slope of the cord
connecting the points (a, f(a)) and (b,f(b)) with a = 3
and b = 5.
f(b) – f(a)
b – a
Using the formula, the slope is
We want the slope of the cord connecting the points
whose x-coordinates are a = 3 and b = 5
f(5) – f(3)
5 – 3
=
=
17 – 5
2
= 6
=
12
2
Slopes and the Difference Quotient

60. Example B.
a. Given f(x) = x2 – 2x + 2, find the slope of the cord
connecting the points (a, f(a)) and (b,f(b)) with a = 3
and b = 5.
f(b) – f(a)
b – a
Using the formula, the slope is
We want the slope of the cord connecting the points
whose x-coordinates are a = 3 and b = 5
f(5) – f(3)
5 – 3
=
=
17 – 5
2
= 6
(5, 17)
(3, 5)
3 5
=
12
2
Slopes and the Difference Quotient

61. Example B.
a. Given f(x) = x2 – 2x + 2, find the slope of the cord
connecting the points (a, f(a)) and (b,f(b)) with a = 3
and b = 5.
f(b) – f(a)
b – a
Using the formula, the slope is
We want the slope of the cord connecting the points
whose x-coordinates are a = 3 and b = 5
f(5) – f(3)
5 – 3
=
=
17 – 5
2
= 6
(5, 17)
(3, 5)
3 5
=
12
2
12
2
slope m = 6
Slopes and the Difference Quotient

62. b. Given f(x) = x2 – 2x + 2, simplify the difference
quotient slope of the cord connecting the points
(a, f(a)) and (b, f(b)).
(b, f(b))
(a, f(a))
a b
f(b)-f(a)
b-a
Slopes and the Difference Quotient

63. b. Given f(x) = x2 – 2x + 2, simplify the difference
quotient slope of the cord connecting the points
(a, f(a)) and (b, f(b)).
f(b) – f(a)
b – a
We are to simplify the 2nd form of the difference
quotient formula with f(x) = x2 – 2x + 2
(b, f(b))
(a, f(a))
a b
f(b)-f(a)
b-a
Slopes and the Difference Quotient

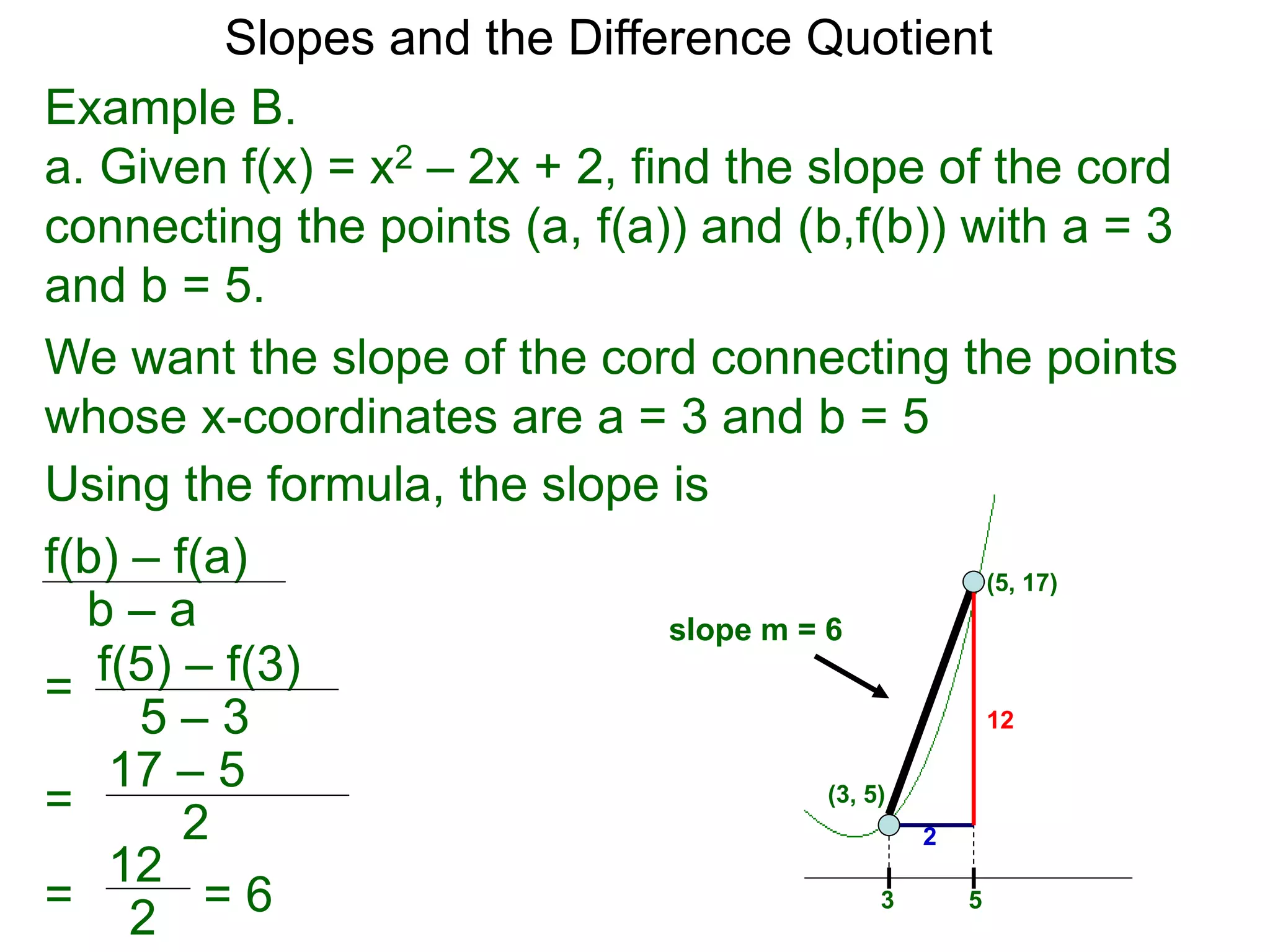
64. b. Given f(x) = x2 – 2x + 2, simplify the difference
quotient slope of the cord connecting the points
(a, f(a)) and (b, f(b)).
f(b) – f(a)
b – a
We are to simplify the 2nd form of the difference
quotient formula with f(x) = x2 – 2x + 2
=
b2 – 2b + 2 – [ a2 – 2a + 2]
b – a
(b, f(b))
(a, f(a))
a b
f(b)-f(a)
b-a
Slopes and the Difference Quotient

65. b. Given f(x) = x2 – 2x + 2, simplify the difference
quotient slope of the cord connecting the points
(a, f(a)) and (b, f(b)).
f(b) – f(a)
b – a
We are to simplify the 2nd form of the difference
quotient formula with f(x) = x2 – 2x + 2
=
b2 – 2b + 2 – [ a2 – 2a + 2]
b – a
=
b2 – a2 – 2b + 2a
b – a
(b, f(b))
(a, f(a))
a b
f(b)-f(a)
b-a
Slopes and the Difference Quotient

66. b. Given f(x) = x2 – 2x + 2, simplify the difference
quotient slope of the cord connecting the points
(a, f(a)) and (b, f(b)).
f(b) – f(a)
b – a
We are to simplify the 2nd form of the difference
quotient formula with f(x) = x2 – 2x + 2
=
b2 – 2b + 2 – [ a2 – 2a + 2]
b – a
=
b2 – a2 – 2b + 2a
b – a
= (b – a)(b + a) – 2(b – a)
b – a
(b, f(b))
(a, f(a))
a b
f(b)-f(a)
b-a
Slopes and the Difference Quotient

67. b. Given f(x) = x2 – 2x + 2, simplify the difference
quotient slope of the cord connecting the points
(a, f(a)) and (b, f(b)).
f(b) – f(a)
b – a
We are to simplify the 2nd form of the difference
quotient formula with f(x) = x2 – 2x + 2
=
b2 – 2b + 2 – [ a2 – 2a + 2]
b – a
=
b2 – a2 – 2b + 2a
b – a
= (b – a)(b + a) – 2(b – a)
b – a
= (b – a) [(b + a) – 2]
b – a
(b, f(b))
(a, f(a))
a b
f(b)-f(a)
b-a
Slopes and the Difference Quotient

68. b. Given f(x) = x2 – 2x + 2, simplify the difference
quotient slope of the cord connecting the points
(a, f(a)) and (b, f(b)).
f(b) – f(a)
b – a
We are to simplify the 2nd form of the difference
quotient formula with f(x) = x2 – 2x + 2
=
b2 – 2b + 2 – [ a2 – 2a + 2]
b – a
=
b2 – a2 – 2b + 2a
b – a
= (b – a)(b + a) – 2(b – a)
b – a
= (b – a) [(b + a) – 2]
b – a
= b + a – 2
(b, f(b))
(a, f(a))
a b
f(b)-f(a)
b-a
Slopes and the Difference Quotient

69. Exercise A.
Given the following f(x), x, and h find f(x+h) – f(x)
1. y = 3x+2, x = 2, h = 0.1 2. y = –2x + 3, x= – 4, h = 0.05
3. y = 2x2 + 1, x = 1, h = 0.1 4. y = –x2 + 3, x= –2, h = –0.2
B. Given the following f(x), simplify Δy = f(x+h) – f(x)
1. y = 3x+2 2. y = –2x + 3
3. y = 2x2 + 1 4. y = –x2 + 3
C. Simplify the difference quotient f(x+h) – f(x)
h
of the following functions that show up in calculus.
“Simplify” in this case means to transform the difference
quotient so the denominator “h” is canceled.
5. y = x2 – x +2 6. y = –x2 + 3x – 1
Slopes and the Difference Quotient
1. y = 2x + 3 2. y = –½ x + 5
3. y = –4x – 3 4. y = mx + b
7. y = – 3x2 – 2x – 4 8. y = ax2 + bx + c

70. Slopes and the Difference Quotient
9. y = 2
x + 3
–1
2 – 3x
16. y = (3 – x)1/2
15. y = x1/2
10. y =
–4
–5 – 3x
11. y = 12. y =ax + b
cx + d
3x – 4
x – 5
13. y = 14. y =
c
ax + b
17. y = (4 – 3x)1/2 18. y = (ax + b)1/2
19. y = 2/(4 + x)1/2 20. y = 3(2x – 3)–1/2
21. y = – 7/(4 – 3x)1/2
22. y = c(ax + b)–1/2
cx + d
3x – 4
x – 5
23. y = 24. y = ax + b
√ √
(Do Long division first)

71. (Answers to odd problems) Exercise A.
1. 𝑓(𝑥 + ℎ)– 𝑓(𝑥) = 0.3 3. 𝑓(𝑥 + ℎ)– 𝑓(𝑥) = 0.42
Exercise B.
1. Δ𝑦 = 3ℎ 3. Δ𝑦 = 2ℎ2 + 4𝑥ℎ
Exercise C.
5.
𝑓 𝑥+ℎ −𝑓(𝑥)
ℎ
= 2𝑥 − 1 + ℎ
1.
𝑓 𝑥+ℎ −𝑓(𝑥)
ℎ
= 2 3.
𝑓 𝑥+ℎ −𝑓(𝑥)
ℎ
= −4
7.
𝑓 𝑥+ℎ −𝑓(𝑥)
ℎ
= −6𝑥 − 3ℎ − 2
9.
𝑓 𝑥+ℎ −𝑓(𝑥)
ℎ
=
−2
(𝑥+3)(𝑥+ℎ+3)
11.
𝑓 𝑥+ℎ −𝑓(𝑥)
ℎ
=
12
(3𝑥+5)(3𝑥+3ℎ+5)
13.
𝑓 𝑥+ℎ −𝑓(𝑥)
ℎ
=
−11
(ℎ+𝑥−5)(𝑥−5)
15.
𝑓 𝑥+ℎ −𝑓(𝑥)
ℎ
=
1
𝑥+ℎ+ 𝑥
Slopes and the Difference Quotient

72. 17.
𝑓 𝑥+ℎ −𝑓(𝑥)
ℎ
=
−3
4−3(𝑥+ℎ)+ 4−3𝑥
19.
𝑓 𝑥+ℎ −𝑓(𝑥)
ℎ
=
−2
4+𝑥 4+𝑥+ℎ( 4+𝑥+ 4+𝑥+ℎ)
21.
𝑓 𝑥+ℎ −𝑓(𝑥)
ℎ
=
−21
4−3𝑥 4−3𝑥−3ℎ( 4−3𝑥+ −3𝑥−3ℎ)
23.
𝑓 𝑥+ℎ −𝑓(𝑥)
ℎ
=
−11
(𝑥−5)(𝑥+ℎ−5)
3𝑥+3ℎ−4
𝑥+ℎ−5
+
3𝑥−4
𝑥−5
Slopes and the Difference Quotient