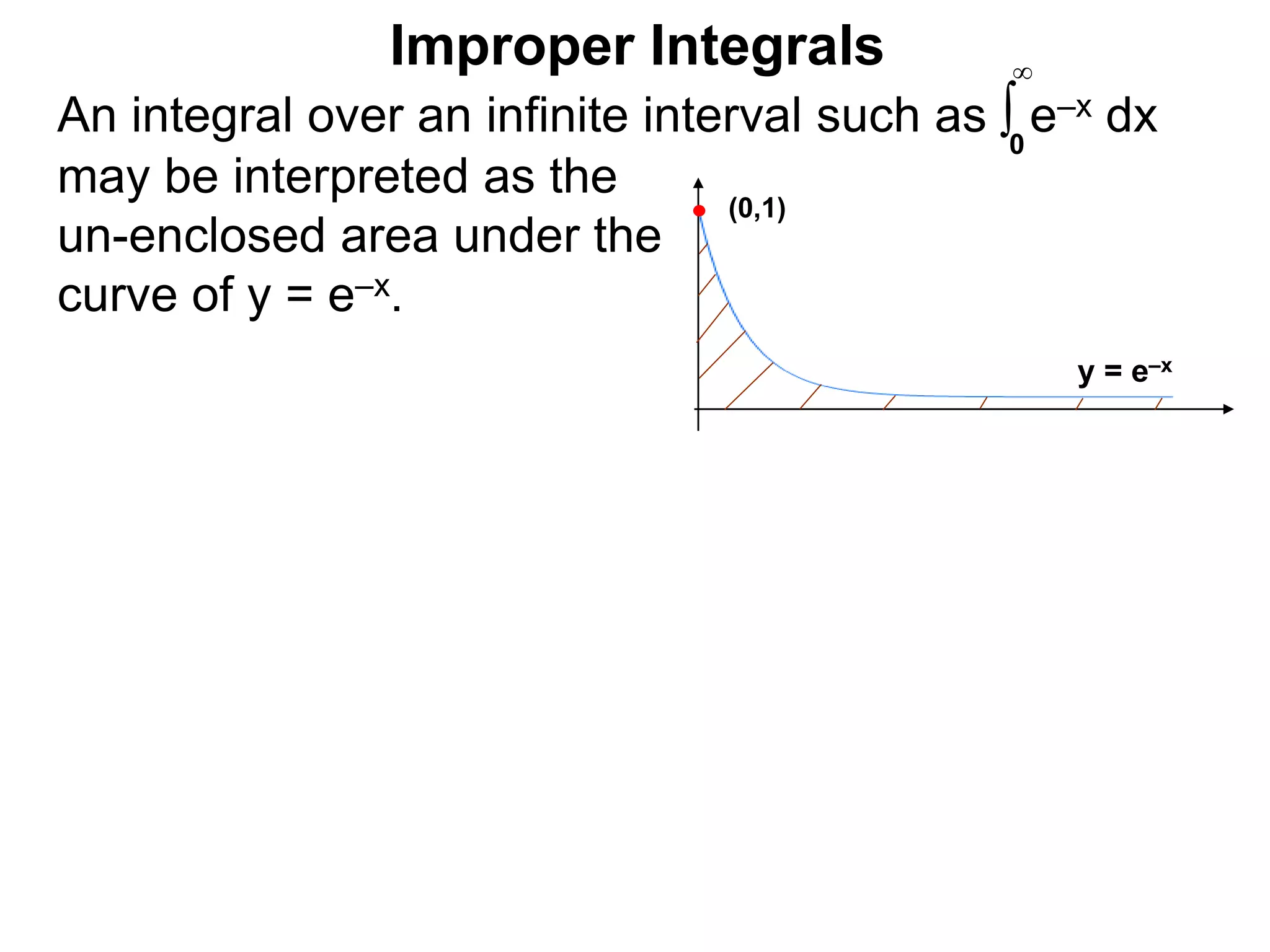
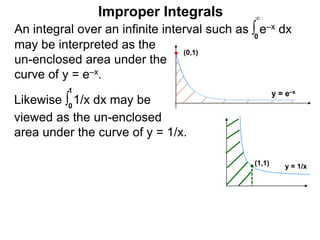
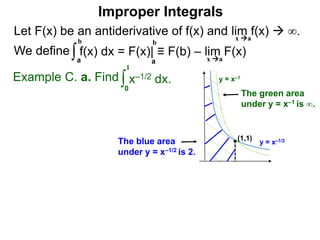
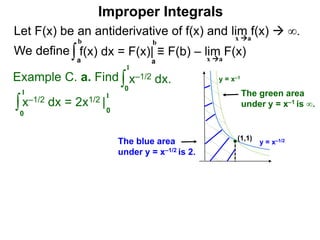
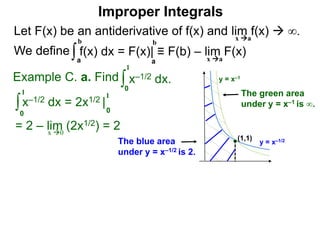
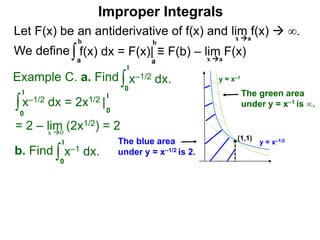
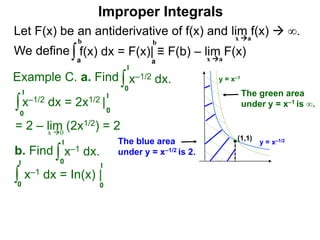
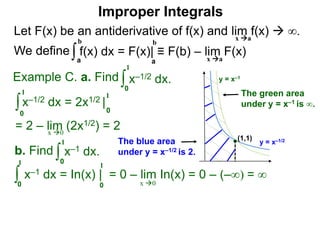
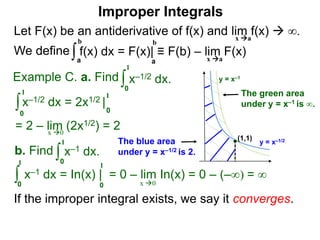
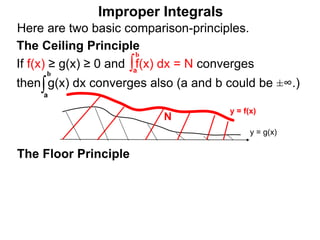
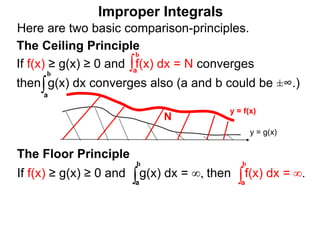
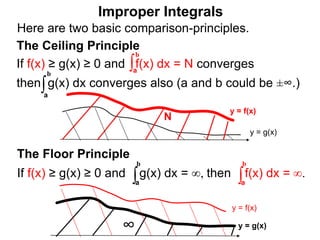
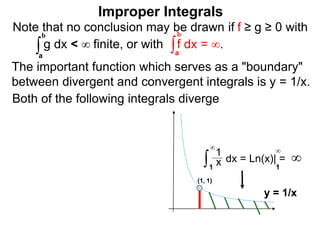
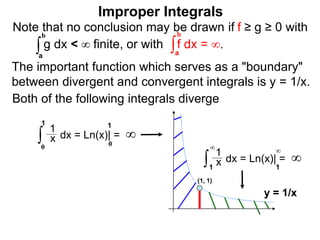
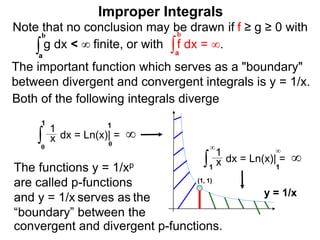
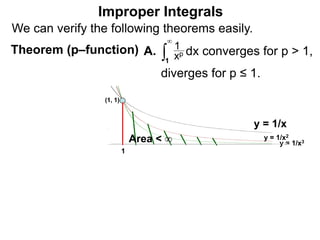
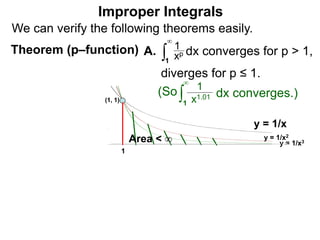
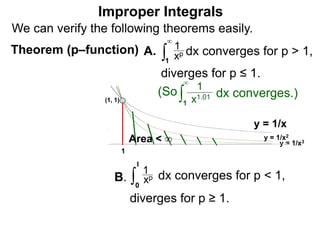
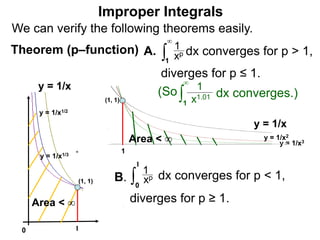
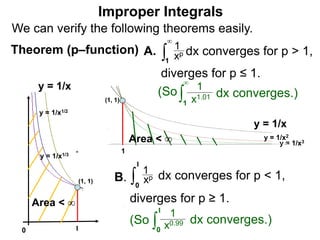
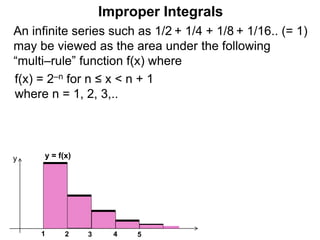
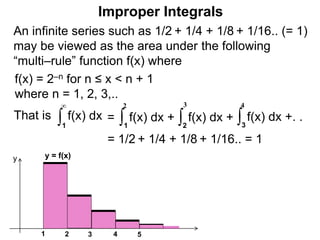
The document discusses improper integrals, which are definite integrals with infinite intervals. An improper integral of a continuous function over an infinite interval, such as ∫ e-x dx from 0 to ∞, or an integral of an unbounded continuous function, such as ∫ 1/x dx from 0 to 1, are called improper integrals. Improper integrals are evaluated by taking the limit of the integral as the interval approaches infinity or by taking the limit of the antiderivative. If the limit exists and is finite, the improper integral converges; if the limit fails to exist or is infinite, the improper integral diverges. Examples are provided to demonstrate the evaluation and convergence of improper integrals.

1. Improper Integrals
An integral over an infinite interval such as ∫ e–x dx
may be interpreted as the
un-enclosed area under the
curve of y = e–x.
0
∞
(0,1)
y = e–x

2. Improper Integrals
An integral over an infinite interval such as ∫ e–x dx
may be interpreted as the
un-enclosed area under the
curve of y = e–x.
0
∞
Likewise ∫ 1/x dx may be
viewed as the un-enclosed
area under the curve of y = 1/x.
0
1
(0,1)
y = e–x
y = 1/x(1,1)

3. Improper Integrals
An integral over an infinite interval such as ∫ e–x dx
may be interpreted as the
un-enclosed area under the
curve of y = e–x.
0
∞
Likewise ∫ 1/x dx may be
viewed as the un-enclosed
area under the curve of y = 1/x.
0
1
(0,1)
y = e–x
Definite integrals of continuous
functions over infinite intervals (a, ∞)
(–∞, a), or (–∞, ∞), such as ∫ e–x dx,
y = 1/x(1,1)
0
∞
or integrals of unbounded continuous functions
such as ∫ 1/x dx are called improper integrals.0
1

4. Improper Integrals
Let f(x) be a continuous function defined for a ≤ x
and F(x) is an antiderivative of f(x).

5. ∫a
∞
lim f(x) dx = F(x)| ≡ lim F(u) – F(a)∫a
u
u ∞ u ∞a
∞
Improper Integrals
Let f(x) be a continuous function defined for a ≤ x
and F(x) is an antiderivative of f(x).
We define the improper (definite) integral
f(x) dx ≡

6. Example A. Find ∫0
∞
e–x dx
∫a
∞
lim f(x) dx = F(x)| ≡ lim F(u) – F(a)∫a
u
u ∞ u ∞a
∞
Improper Integrals
Let f(x) be a continuous function defined for a ≤ x
and F(x) is an antiderivative of f(x).
We define the improper (definite) integral
f(x) dx ≡

7. Example A. Find ∫0
∞
e–x dx
∫0
∞
e–x dx = –e–x|
0
∞
∫a
∞
lim f(x) dx = F(x)| ≡ lim F(u) – F(a)∫a
u
u ∞ u ∞a
∞
Improper Integrals
Let f(x) be a continuous function defined for a ≤ x
and F(x) is an antiderivative of f(x).
We define the improper (definite) integral
f(x) dx ≡

8. Example A. Find ∫0
∞
e–x dx
∫0
∞
e–x dx = –e–x| = lim (–e–x) – (–e0) = 1
x ∞0
∞
∫a
∞
lim f(x) dx = F(x)| ≡ lim F(u) – F(a)∫a
u
u ∞ u ∞a
∞
Improper Integrals
Let f(x) be a continuous function defined for a ≤ x
and F(x) is an antiderivative of f(x).
We define the improper (definite) integral
f(x) dx ≡

9. Example A. Find ∫0
∞
e–x dx
∫0
∞
e–x dx = –e–x| = lim (–e–x) – (–e0) = 1
x ∞0
∞
∫a
∞
lim f(x) dx = F(x)| ≡ lim F(u) – F(a)∫a
u
u ∞ u ∞a
∞
Improper Integrals
Let f(x) be a continuous function defined for a ≤ x
and F(x) is an antiderivative of f(x).
We define the improper (definite) integral
f(x) dx ≡
Similarly for a continuous function f(x) where x ≤ a,
we define the improper (definite) integral
∫–∞
lim f(x) dx = F(x)| ≡ lim F(a) – F(u)∫u
a
u –∞ u –∞
a
–∞
f(x) dx ≡
a

10. Example A. Find ∫0
∞
e–x dx
∫0
∞
e–x dx = –e–x| = lim (–e–x) – (–e0) = 1
x ∞0
∞
∫a
∞
lim f(x) dx = F(x)| ≡ lim F(u) – F(a)∫a
u
u ∞ u ∞a
∞
Improper Integrals
Let f(x) be a continuous function defined for a ≤ x
and F(x) is an antiderivative of f(x).
We define the improper (definite) integral
f(x) dx ≡
Similarly for a continuous function f(x) where x ≤ a,
we define the improper (definite) integral
∫–∞
lim f(x) dx = F(x)| ≡ lim F(a) – F(u)∫u
a
u –∞ u –∞
a
–∞
f(x) dx ≡
a
Example B. Find ∫ cos(x)dx
–∞
0

11. Example A. Find ∫0
∞
e–x dx
∫0
∞
e–x dx = –e–x| = lim (–e–x) – (–e0) = 1
x ∞0
∞
∫a
∞
lim f(x) dx = F(x)| ≡ lim F(u) – F(a)∫a
u
u ∞ u ∞a
∞
Improper Integrals
Let f(x) be a continuous function defined for a ≤ x
and F(x) is an antiderivative of f(x).
We define the improper (definite) integral
f(x) dx ≡
Similarly for a continuous function f(x) where x ≤ a,
we define the improper (definite) integral
∫–∞
lim f(x) dx = F(x)| ≡ lim F(a) – F(u)∫u
a
u –∞ u –∞
a
–∞
f(x) dx ≡
a
Example B. Find ∫ cos(x)dx
∫
0
cos(x)dx = sin(x) |
–∞
0
–∞ –∞
0

12. Example A. Find ∫0
∞
e–x dx
∫0
∞
e–x dx = –e–x| = lim (–e–x) – (–e0) = 1
x ∞0
∞
∫a
∞
lim f(x) dx = F(x)| ≡ lim F(u) – F(a)∫a
u
u ∞ u ∞a
∞
Improper Integrals
Let f(x) be a continuous function defined for a ≤ x
and F(x) is an antiderivative of f(x).
We define the improper (definite) integral
f(x) dx ≡
Similarly for a continuous function f(x) where x ≤ a,
we define the improper (definite) integral
∫–∞
lim f(x) dx = F(x)| ≡ lim F(a) – F(u)∫u
a
u –∞ u –∞
a
–∞
f(x) dx ≡
a
Example B. Find ∫ cos(x)dx
∫
0
cos(x)dx = sin(x) | = lim sin(0) – sin(x) which is UDF.
x –∞
–∞
0
–∞ –∞
0

13. Let F(x) be an antiderivative of f(x) and lim f(x)  ∞.
We define
x a
∫a
b
f(x) dx = F(x)| ≡ F(b) – lim F(x)
a
b
Improper Integrals
x a

14. Let F(x) be an antiderivative of f(x) and lim f(x)  ∞.
We define
x a
∫a
b
f(x) dx = F(x)| ≡ F(b) – lim F(x)
Example C. a. Find ∫0
1
x–1/2 dx.
a
b
Improper Integrals
x a

15. Let F(x) be an antiderivative of f(x) and lim f(x)  ∞.
We define
x a
∫a
b
f(x) dx = F(x)| ≡ F(b) – lim F(x)
Example C. a. Find ∫0
1
x–1/2 dx.
a
b
Improper Integrals
x a
y = x–1/2
y = x–1
(1,1)
The green area
under y = x–1 is ∞.
The blue area
under y = x–1/2 is 2.

16. Let F(x) be an antiderivative of f(x) and lim f(x)  ∞.
We define
x a
∫a
b
f(x) dx = F(x)| ≡ F(b) – lim F(x)
Example C. a. Find ∫0
1
x–1/2 dx.
∫0
1
x–1/2 dx = 2x1/2 |
1
0
a
b
Improper Integrals
x a
y = x–1/2
y = x–1
(1,1)
The blue area
under y = x–1/2 is 2.
The green area
under y = x–1 is ∞.

17. Let F(x) be an antiderivative of f(x) and lim f(x)  ∞.
We define
x a
∫a
b
f(x) dx = F(x)| ≡ F(b) – lim F(x)
Example C. a. Find ∫0
1
x–1/2 dx.
∫0
1
x–1/2 dx = 2x1/2 |
1
0
x 0
a
b
Improper Integrals
x a
y = x–1/2
y = x–1
(1,1)
The blue area
under y = x–1/2 is 2.
The green area
under y = x–1 is ∞.
= 2 – lim (2x1/2) = 2

18. Let F(x) be an antiderivative of f(x) and lim f(x)  ∞.
We define
x a
∫a
b
f(x) dx = F(x)| ≡ F(b) – lim F(x)
Example C. a. Find ∫0
1
x–1/2 dx.
∫0
1
x–1/2 dx = 2x1/2 |
1
0
x 0
b. Find ∫0
1
x–1 dx.
a
b
Improper Integrals
x a
y = x–1/2
y = x–1
(1,1)
The blue area
under y = x–1/2 is 2.
The green area
under y = x–1 is ∞.
= 2 – lim (2x1/2) = 2

19. Let F(x) be an antiderivative of f(x) and lim f(x)  ∞.
We define
x a
∫a
b
f(x) dx = F(x)| ≡ F(b) – lim F(x)
Example C. a. Find ∫0
1
x–1/2 dx.
∫0
1
x–1/2 dx = 2x1/2 |
1
0
x 0
b. Find ∫0
1
x–1 dx.
∫0
1
x–1 dx = In(x) |
1
0
a
b
Improper Integrals
x a
y = x–1/2
y = x–1
(1,1)
The blue area
under y = x–1/2 is 2.
The green area
under y = x–1 is ∞.
= 2 – lim (2x1/2) = 2

20. Let F(x) be an antiderivative of f(x) and lim f(x)  ∞.
We define
x a
∫a
b
f(x) dx = F(x)| ≡ F(b) – lim F(x)
Example C. a. Find ∫0
1
x–1/2 dx.
∫0
1
x–1/2 dx = 2x1/2 |
1
0
x 0
b. Find ∫0
1
x–1 dx.
∫0
1
x–1 dx = In(x) | = 0 – lim In(x) = 0 – (–∞) = ∞
1
0 x 0
a
b
Improper Integrals
x a
y = x–1/2
y = x–1
(1,1)
The blue area
under y = x–1/2 is 2.
The green area
under y = x–1 is ∞.
= 2 – lim (2x1/2) = 2

21. Let F(x) be an antiderivative of f(x) and lim f(x)  ∞.
We define
x a
∫a
b
f(x) dx = F(x)| ≡ F(b) – lim F(x)
Example C. a. Find ∫0
1
x–1/2 dx.
∫0
1
x–1/2 dx = 2x1/2 |
1
0
x 0
b. Find ∫0
1
x–1 dx.
∫0
1
x–1 dx = In(x) | = 0 – lim In(x) = 0 – (–∞) = ∞
1
0 x 0
If the improper integral exists, we say it converges.
a
b
Improper Integrals
x a
y = x–1/2
y = x–1
(1,1)
The blue area
under y = x–1/2 is 2.
The green area
under y = x–1 is ∞.
= 2 – lim (2x1/2) = 2

22. Let F(x) be an antiderivative of f(x) and lim f(x)  ∞.
We define
x a
∫a
b
f(x) dx = F(x)| ≡ F(b) – lim F(x)
Example C. a. Find ∫0
1
x–1/2 dx.
∫0
1
x–1/2 dx = 2x1/2 |
1
0
x 0
b. Find ∫0
1
x–1 dx.
∫0
1
x–1 dx = In(x) | = 0 – lim In(x) = 0 – (–∞) = ∞
1
0 x 0
If the improper integral exists, we say it converges.
If the improper integral fails to exist or it´s infinite,
we say it diverges.
a
b
Improper Integrals
x a
y = x–1/2
y = x–1
(1,1)
The blue area
under y = x–1/2 is 2.
The green area
under y = x–1 is ∞.
= 2 – lim (2x1/2) = 2

23. Let f(x) be a continuous function defined for all x’s,
and F´(x) = f(x), we define the improper integral
∫ f(x)dx ≡ lim
Improper Integrals
–∞
∞
∫f(x) dx
–u
u
In the situations that we can’t find the anti-derivative
F(x) or the numerical answers, the next question is
to determine if the integrals converge or diverge
by comparing them to other known integrals.
Find ∫Example D.
–∞
∞
∫ 1/(1 + x2) dx
–∞
∞
= lim tan–1(u) – tan–1(–u)
= π/2 + π/2 = π.
u ∞
y = 1/(1 + x2)1/(1 + x2)dx
x
u∞
= lim F(u) – F(–u).u∞
–x
= lim tan–1(x) l–u
u
u ∞

24. Let f(x) be a continuous function defined for all x’s,
and F´(x) = f(x), we define the improper integral
∫ f(x)dx ≡ lim
Improper Integrals
–∞
∞
∫f(x) dx
–u
u
u∞
= lim F(u) – F(–u).u∞

25. Let f(x) be a continuous function defined for all x’s,
and F´(x) = f(x), we define the improper integral
∫ f(x)dx ≡ lim
Improper Integrals
–∞
∞
∫f(x) dx
–u
u
Find ∫Example D.
–∞
∞
1/(1 + x2)dx
u∞
= lim F(u) – F(–u).u∞

26. Let f(x) be a continuous function defined for all x’s,
and F´(x) = f(x), we define the improper integral
∫ f(x)dx ≡ lim
Improper Integrals
–∞
∞
∫f(x) dx
–u
u
Find ∫Example D.
–∞
∞
y = 1/(1 + x2)1/(1 + x2)dx
x
u∞
= lim F(u) – F(–u).u∞
–x

27. Let f(x) be a continuous function defined for all x’s,
and F´(x) = f(x), we define the improper integral
∫ f(x)dx ≡ lim
Improper Integrals
–∞
∞
∫f(x) dx
–u
u
Find ∫Example D.
–∞
∞
∫ 1/(1 + x2) dx
–∞
∞
u ∞
y = 1/(1 + x2)1/(1 + x2)dx
x
u∞
= lim F(u) – F(–u).u∞
–x
= lim tan–1(x) l–u
u

28. Let f(x) be a continuous function defined for all x’s,
and F´(x) = f(x), we define the improper integral
∫ f(x)dx ≡ lim
Improper Integrals
–∞
∞
∫f(x) dx
–u
u
Find ∫Example D.
–∞
∞
∫ 1/(1 + x2) dx
–∞
∞
= lim tan–1(u) – tan–1(–u)
u ∞
y = 1/(1 + x2)1/(1 + x2)dx
x
u∞
= lim F(u) – F(–u).u∞
–x
= lim tan–1(x) l–u
u
u ∞

29. Let f(x) be a continuous function defined for all x’s,
and F´(x) = f(x), we define the improper integral
∫ f(x)dx ≡ lim
Improper Integrals
–∞
∞
∫f(x) dx
–u
u
Find ∫Example D.
–∞
∞
∫ 1/(1 + x2) dx
–∞
∞
= lim tan–1(u) – tan–1(–u)
= π/2 + π/2 = π.
u ∞
y = 1/(1 + x2)1/(1 + x2)dx
x
u∞
= lim F(u) – F(–u).u∞
–x
= lim tan–1(x) l–u
u
u ∞

30. Let f(x) be a continuous function defined for all x’s,
and F´(x) = f(x), we define the improper integral
∫ f(x)dx ≡ lim
Improper Integrals
–∞
∞
∫f(x) dx
–u
u
In the situations that we can’t find the anti-derivative
F(x) or the numerical answers, the next question is
to determine if the integrals converge or diverge
by comparing them to other known integrals.
Find ∫Example D.
–∞
∞
∫ 1/(1 + x2) dx
–∞
∞
= lim tan–1(u) – tan–1(–u)
= π/2 + π/2 = π.
u ∞
y = 1/(1 + x2)1/(1 + x2)dx
x
u∞
= lim F(u) – F(–u).u∞
–x
= lim tan–1(x) l–u
u
u ∞

31. The Floor Principle
Improper Integrals
The Ceiling Principle
Here are two basic comparison-principles.

32. The Floor Principle
Improper Integrals
The Ceiling Principle
If f(x) ≥ g(x) ≥ 0 and f(x) dx = N converges
then g(x) dx converges also (a and b could be ±∞.)
∫a
b
∫a
b
Here are two basic comparison-principles.

33. The Floor Principle
Improper Integrals
The Ceiling Principle
If f(x) ≥ g(x) ≥ 0 and f(x) dx = N converges
then g(x) dx converges also (a and b could be ±∞.)
∫a
b
∫a
b
y = f(x)
y = g(x)
N
Here are two basic comparison-principles.

34. The Floor Principle
If f(x) ≥ g(x) ≥ 0 and g(x) dx = ∞, then f(x) dx = ∞.∫a
b
∫a
b
Improper Integrals
The Ceiling Principle
If f(x) ≥ g(x) ≥ 0 and f(x) dx = N converges
then g(x) dx converges also (a and b could be ±∞.)
∫a
b
∫a
b
y = f(x)
y = g(x)
N
Here are two basic comparison-principles.

35. The Floor Principle
If f(x) ≥ g(x) ≥ 0 and g(x) dx = ∞, then f(x) dx = ∞.∫a
b
∫a
b
y = f(x)
y = g(x)∞
Improper Integrals
The Ceiling Principle
If f(x) ≥ g(x) ≥ 0 and f(x) dx = N converges
then g(x) dx converges also (a and b could be ±∞.)
∫a
b
∫a
b
y = f(x)
y = g(x)
N
Here are two basic comparison-principles.

36. Note that no conclusion may be drawn if f ≥ g ≥ 0 with
g dx < ∞ finite, or with f dx = ∞.∫a
b
∫a
b
Improper Integrals

37. The important function which serves as a "boundary"
between divergent and convergent integrals is y = 1/x.
Note that no conclusion may be drawn if f ≥ g ≥ 0 with
g dx < ∞ finite, or with f dx = ∞.∫a
b
∫a
b
Improper Integrals

38. The important function which serves as a "boundary"
between divergent and convergent integrals is y = 1/x.
Note that no conclusion may be drawn if f ≥ g ≥ 0 with
g dx < ∞ finite, or with f dx = ∞.∫a
b
∫a
b
Improper Integrals
(1, 1)
Both of the following integrals diverge
∫1
∞
x
1
dx = Ln(x)| = ∞
1
∞
y = 1/x

39. The important function which serves as a "boundary"
between divergent and convergent integrals is y = 1/x.
Note that no conclusion may be drawn if f ≥ g ≥ 0 with
g dx < ∞ finite, or with f dx = ∞.∫a
b
∫a
b
Improper Integrals
∫
1
0
x
1
dx = Ln(x)| = ∞
(1, 1)
Both of the following integrals diverge
∫1
∞
x
1
dx = Ln(x)| = ∞
1
∞
1
0
y = 1/x

40. The important function which serves as a "boundary"
between divergent and convergent integrals is y = 1/x.
Note that no conclusion may be drawn if f ≥ g ≥ 0 with
g dx < ∞ finite, or with f dx = ∞.∫a
b
∫a
b
Improper Integrals
∫
1
0
x
1
dx = Ln(x)| = ∞
(1, 1)
Both of the following integrals diverge
∫1
∞
x
1
dx = Ln(x)| = ∞
1
∞
1
0
y = 1/x
The functions y = 1/xp
are called p-functions
and y = 1/x serves as the
“boundary” between the
convergent and divergent p-functions.

41. Theorem (p–function) ∫1
xp
1
∞
dx converges for p > 1,A.
Improper Integrals
diverges for p ≤ 1.
We can verify the following theorems easily.

42. Theorem (p–function) ∫1
xp
1
∞
dx converges for p > 1,A.
Improper Integrals
(1, 1)
y = 1/x
y = 1/x2
y = 1/x3
1
Area < ∞
diverges for p ≤ 1.
We can verify the following theorems easily.

43. Theorem (p–function) ∫1
xp
1
∞
dx converges for p > 1,A.
Improper Integrals
(1, 1)
y = 1/x
y = 1/x2
y = 1/x3
1
Area < ∞
diverges for p ≤ 1.
We can verify the following theorems easily.
(So ∫1 x1.01
1∞
dx converges.)

44. Theorem (p–function) ∫1
xp
1
∞
dx converges for p > 1,A.
Improper Integrals
(1, 1)
y = 1/x
y = 1/x2
y = 1/x3
1
Area < ∞
diverges for p ≤ 1.
We can verify the following theorems easily.
(So ∫1 x1.01
1∞
dx converges.)
∫ xp
1
dx converges for p < 1,B.
0
1
diverges for p ≥ 1.

45. Theorem (p–function) ∫1
xp
1
∞
dx converges for p > 1,A.
Improper Integrals
0 1
(1, 1)
y = 1/x
y = 1/x2
y = 1/x3
1
Area < ∞
Area < ∞
y = 1/x1/2
y = 1/x
y = 1/x1/3
diverges for p ≤ 1.
(1, 1)
We can verify the following theorems easily.
(So ∫1 x1.01
1∞
dx converges.)
∫ xp
1
dx converges for p < 1,B.
0
1
diverges for p ≥ 1.

46. Theorem (p–function) ∫1
xp
1
∞
dx converges for p > 1,A.
Improper Integrals
0 1
(1, 1)
y = 1/x
y = 1/x2
y = 1/x3
1
Area < ∞
Area < ∞
y = 1/x1/2
y = 1/x
y = 1/x1/3
diverges for p ≤ 1.
(1, 1)
We can verify the following theorems easily.
(So ∫1 x1.01
1∞
dx converges.)
∫ xp
1
dx converges for p < 1,B.
0
1
diverges for p ≥ 1.
(So ∫ x0.99
1
dx converges.)
0
1

47. Improper Integrals
∫
Example E. Determine if the integral converges or
diverges using the comparison principle.
∞
1
1/(1 + x + x3/2) dxa.
∫0
1
2/(x3 + x2 )dxb.

48. Improper Integrals
∫
Example E. Determine if the integral converges or
diverges using the comparison principle.
∞
1
1/(1 + x + x3/2) dxa.
∫0
1
2/(x3 + x2 )dxb.
Since 1/(1 + x + x3/2) < 1/x3/2 for 1 < x,

49. Improper Integrals
∫
Example E. Determine if the integral converges or
diverges using the comparison principle.
∞
1
1/(1 + x + x3/2) dxa.
∫0
1
2/(x3 + x2 )dxb.
Since 1/(1 + x + x3/2) < 1/x3/2 for 1 < x,
so 1/(1 + x + x3/2) dx < 1/x3/2 dx∫
∞
1
∫
∞
1

50. Improper Integrals
∫
Example E. Determine if the integral converges or
diverges using the comparison principle.
∞
1
1/(1 + x + x3/2) dxa.
∫0
1
2/(x3 + x2 )dxb.
Since 1/(1 + x + x3/2) < 1/x3/2 for 1 < x,
so 1/(1 + x + x3/2) dx < 1/x3/2 dx < ∞ converges.∫
∞
1
∫
∞
1

51. Improper Integrals
∫
Example E. Determine if the integral converges or
diverges using the comparison principle.
∞
1
1/(1 + x + x3/2) dxa.
∫0
1
2/(x3 + x2 )dxb.
Since 1/(1 + x + x3/2) < 1/x3/2 for 1 < x,
so 1/(1 + x + x3/2) dx < 1/x3/2 dx < ∞ converges.∫
∞
1
∫
∞
1
2
x3 + x2 = 2
x2(x + 1)
For 0 < x < 1,

52. Improper Integrals
∫
Example E. Determine if the integral converges or
diverges using the comparison principle.
∞
1
1/(1 + x + x3/2) dxa.
∫0
1
2/(x3 + x2 )dxb.
Since 1/(1 + x + x3/2) < 1/x3/2 for 1 < x,
so 1/(1 + x + x3/2) dx < 1/x3/2 dx < ∞ converges.∫
∞
1
∫
∞
1
2
x3 + x2 = 2
x2(x + 1)
>
1
x2For 0 < x < 1,
1

53. Improper Integrals
∫
Example E. Determine if the integral converges or
diverges using the comparison principle.
∞
1
1/(1 + x + x3/2) dxa.
∫0
1
2/(x3 + x2 )dxb.
Since 1/(1 + x + x3/2) < 1/x3/2 for 1 < x,
so 1/(1 + x + x3/2) dx < 1/x3/2 dx < ∞ converges.∫
∞
1
∫
∞
1
2
x3 + x2 = 2
x2(x + 1)
>
1
x2For 0 < x < 1,
1
so 2/(x3 + x2)dx >∫0
1
∫0
1
1/x2 dx

54. Improper Integrals
∫
Example E. Determine if the integral converges or
diverges using the comparison principle.
∞
1
1/(1 + x + x3/2) dxa.
∫0
1
2/(x3 + x2 )dxb.
Since 1/(1 + x + x3/2) < 1/x3/2 for 1 < x,
so 1/(1 + x + x3/2) dx < 1/x3/2 dx < ∞ converges.∫
∞
1
∫
∞
1
2
x3 + x2 = 2
x2(x + 1)
>
1
x2For 0 < x < 1,
1
so 2/(x3 + x2)dx >∫0
1
∫0
1
1/x2 dx = ∞ and it diverges.

55. An infinite series such as 1/2 + 1/4 + 1/8 + 1/16.. (= 1)
may be viewed as the area under the following
“multi–rule” function f(x) where
f(x) = 2–n for n ≤ x < n + 1
where n = 1, 2, 3,..
1
y = f(x)
2 3 4
y
5
Improper Integrals

56. An infinite series such as 1/2 + 1/4 + 1/8 + 1/16.. (= 1)
may be viewed as the area under the following
“multi–rule” function f(x) where
f(x) = 2–n for n ≤ x < n + 1
where n = 1, 2, 3,..
1
y = f(x)
2 3 4
y
5
That is ∫1
∞
f(x) dx
= 1/2 + 1/4 + 1/8 + 1/16.. = 1
∫1
2
f(x) dx + ∫2
3
f(x) dx + ∫3
4
f(x) dx +. .=
Improper Integrals

57. An infinite series such as 1/2 + 1/4 + 1/8 + 1/16.. (= 1)
may be viewed as the area under the following
“multi–rule” function f(x) where
f(x) = 2–n for n ≤ x < n + 1
where n = 1, 2, 3,..
1
y = f(x)
2 3 4
y
5
That is ∫1
∞
f(x) dx
= 1/2 + 1/4 + 1/8 + 1/16.. = 1
∫1
2
f(x) dx + ∫2
3
f(x) dx + ∫3
4
f(x) dx +. .=
In the next section, we establish the
relation between summing series
versus integrating functions,
i.e. the discrete vs. the continuous.
Improper Integrals