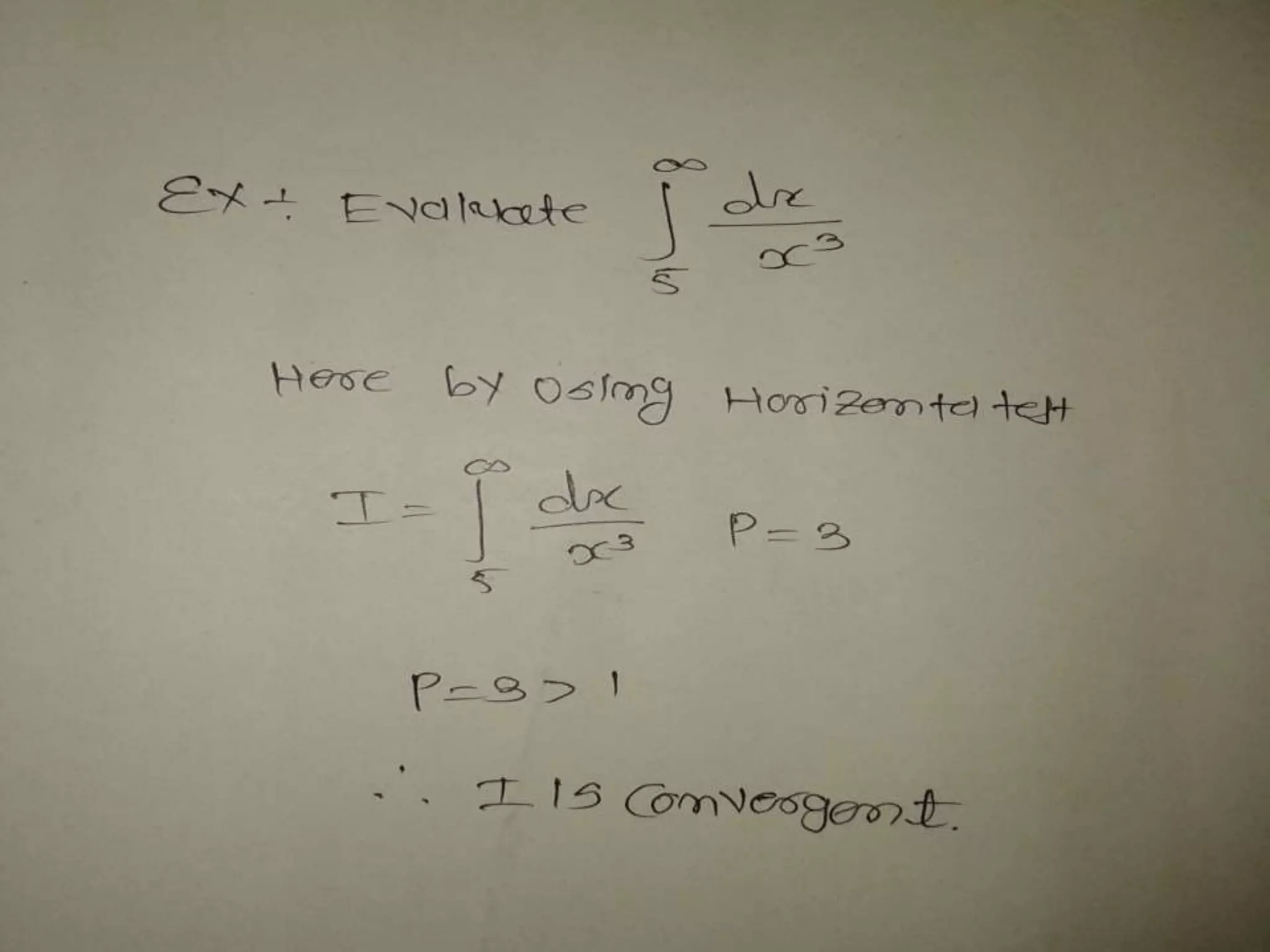This document discusses improper integrals, which are integrals with infinite limits of integration or an integrand that is unbounded within the limits. There are four types of improper integrals: 1) when the upper limit is infinity, 2) when the lower limit is infinity, 3) when both limits are infinity, and 4) when the integral is unbounded. The document provides examples of each type and explains that an improper integral converges if the limit exists as the limiting value is approached, and diverges if the limit does not exist. Tests for convergence like the p-integral test are also mentioned.

1. Calculus

2. Guidance by – MAULIK PRAJAPATI
Presented by
 KRISNADITYA RANA
YATIN DESAI
LAKSHMI VIMAL
KISHAN PATEL
SAGRIKA MAURYA
SHREY PATEL
140750116048
140750111001
140750111002
140750111004
140750111003
140750111005

3.  In most of applications of engineering and science there occurs
special functions, like gamma functions ,beta functions etc , which are in
the form of integrals which are of special types in which the limits of
integration are infinity or the integrand becomes unbounded within
the limits . Such type of integrals are known as improper integrals.
Convergence of such integrals has an important and main roll rather
than divergent integral .

we shall discuss about the type of improper integrals

4.  The definite integral is said to be improper integral if one or both limits
of integration are infinite and/or if the integrand integral is unbounded
on the interval
EXAMPAL

5. TYPES OF INTEGRALS
1) When upper limit is infinity
2) When lower limit is infinity
3) When both limits of integration are infinity
4) When integral is Unbounded

6. 1) When upper limit is infinity
Now is F is Continuous on an interval [a,….) then an improper integral can be define as follow
If this limit exist , we say that Iis Convergent; if not , it is divergent

7. EXAMPAL

8. Now is F is Continuous on an interval (..,b] then an improper integral can be define as
follow
If this limit exist , we say that Iis Convergent; if not , it is divergent

9. EXAMPAL

10. Now is F is Continuous on an interval (..,b] then an improper integral can be define as follow
If this limit exist , we say that Iis Convergent; if not , it is divergent

11. EXAMPAL

12. A) If f(x) is continuous on [ a , b)
If limit exist Integral is Converges , otherwise it is diverges.

13. B) If f(x) is continuous on ( a , b]
If limit exist Integral is Converges , otherwise it is diverges.

14. C) If f(x) is continuous on [ a , b] and not bounded at
the point C E ( a ,b) then we can write
If limit exist Integral is Converges , otherwise it is diverges.

15. Horizontal P-integral test
The integral
1. Converges if P > 1
2. Diverges if P < 1_

16. Vertical P-integral test
1. Converges if P < 1
2. Diverges if P > 1
The integral
_

18. Thanks for
your
anticipation