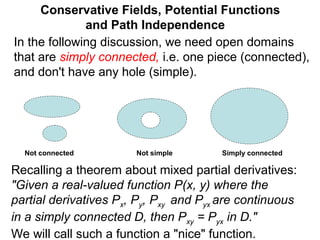
The document discusses conservative vector fields and potential functions. It defines a conservative field as one that is the gradient of a "nice" function, where the mixed partial derivatives are equal. A theorem is presented stating that a vector field F is conservative if and only if its partial derivatives satisfy fy = gx. An example shows a given vector field is conservative by verifying this condition. The potential function for the example field is then found by partial integration.

1. Conservative Fields, Potential Functions
and Path Independence

2. Conservative Fields, Potential Functions
and Path Independence
In the following discussion, we need open domains
that are simply connected, i.e. one piece (connected),
and don't have any hole (simple).

3. Conservative Fields, Potential Functions
and Path Independence
In the following discussion, we need open domains
that are simply connected, i.e. one piece (connected),
and don't have any hole (simple).
Not simpleNot connected Simply connected

4. Conservative Fields, Potential Functions
and Path Independence
In the following discussion, we need open domains
that are simply connected, i.e. one piece (connected),
and don't have any hole (simple).
Not simpleNot connected Simply connected
Recalling a theorem about mixed partial derivatives:
"Given a real-valued function P(x, y) where the
partial derivatives Px, Py, Pxy and Pyx are continuous
in a simply connected D, then Pxy = Pyx in D."

5. Conservative Fields, Potential Functions
and Path Independence
In the following discussion, we need open domains
that are simply connected, i.e. one piece (connected),
and don't have any hole (simple).
Not simpleNot connected Simply connected
Recalling a theorem about mixed partial derivatives:
"Given a real-valued function P(x, y) where the
partial derivatives Px, Py, Pxy and Pyx are continuous
in a simply connected D, then Pxy = Pyx in D."
We will call such a function a "nice" function.

6. Conservative Fields, Potential Functions
and Path Independence
Given a nice function P(x, y), its gradients F= P(x, y)
is a vector field.

7. Conservative Fields, Potential Functions
and Path Independence
Given a nice function P(x, y), its gradients F= P(x, y)
is a vector field. (Recall that P(x, y) = fxi + fyj).

8. Given a nice function P(x, y), its gradients F= P(x, y)
is a vector field. (Recall that P(x, y) = fxi + fyj).
P(x, y) is said to be a potential function of the field F.
Conservative Fields, Potential Functions
and Path Independence

9. Given a nice function P(x, y), its gradients F= P(x, y)
is a vector field. (Recall that P(x, y) = Pxi + Pyj).
P(x, y) is said to be a potential function of the field F.
Conservative Fields, Potential Functions
and Path Independence
A vector field F that is the gradient field of a "nice"
function P(x, y) is called a conservative field.

10. Conservative Fields, Potential Functions
and Path Independence
A vector field F that is the gradient field of a "nice"
function P(x, y) is called a conservative field.
Given an arbitrary vector field F, we like to know if it
is conservative, that is, if there is a potential function
P whose gradient is F.
Given a nice function P(x, y), its gradients F= P(x, y)
is a vector field. (Recall that P(x, y) = Pxi + Pyj).
P(x, y) is said to be a potential function of the field F.

11. Theorem: Given a vector field F = f(x, y)i + g(x, y)j
with f and g having continuous first partial derivatives
(in a open simply connected region) is conservative
if and only if fy = gx.
Conservative Fields, Potential Functions
and Path Independence
A vector field F that is the gradient field of a "nice"
function P(x, y) is called a conservative field.
Given an arbitrary vector field F, we like to know if it
is conservative, that is, if there is a potential function
P whose gradient is F.
Given a nice function P(x, y), its gradients F= P(x, y)
is a vector field. (Recall that P(x, y) = Pxi + Pyj).
P(x, y) is said to be a potential function of the field F.

12. Conservative Fields, Potential Functions
and Path Independence
If a function P(x, y) is a "nice" function, its gradient
field P(x, y) = Pxi + Pyj satisfy Pxy = Pyx since the
mixed partials are the same.

13. This theorem gives the converse of the above fact.
Conservative Fields, Potential Functions
and Path Independence
If a function P(x, y) is a "nice" function, its gradient
field P(x, y) = Pxi + Pyj satisfy Pxy = Pyx since the
mixed partials are the same.

14. This theorem gives the converse of the above fact.
Conservative Fields, Potential Functions
and Path Independence
If a function P(x, y) is a "nice" function, its gradient
field P(x, y) = Pxi + Pyj satisfy Pxy = Pyx since the
mixed partials are the same.
If a vector field F = fi + gj satisfy fy = gx and they are
continuous, then F is the gradient field of a "nice"
function P(x, y).

15. This theorem gives the converse of the above fact.
Conservative Fields, Potential Functions
and Path Independence
If a function P(x, y) is a "nice" function, its gradient
field P(x, y) = Pxi + Pyj satisfy Pxy = Pyx since the
mixed partials are the same.
If a vector field F = fi + gj satisfy fy = gx and they are
continuous, then F is the gradient field of a "nice"
function P(x, y).
Example: a. Show the vector field
F(x, y) = xy2
i + (y + yx2
)j is conservative.

16. This theorem gives the converse of the above fact.
Conservative Fields, Potential Functions
and Path Independence
If a function P(x, y) is a "nice" function, its gradient
field P(x, y) = Pxi + Pyj satisfy Pxy = Pyx since the
mixed partials are the same.
If a vector field F = fi + gj satisfy fy = gx and they are
continuous, then F is the gradient field of a "nice"
function P(x, y).
Example: a. Show the vector field
F(x, y) = xy2
i + (y + yx2
)j is conservative.
f(x, y) = xy2
, g(x, y) = y + yx2

17. This theorem gives the converse of the above fact.
Conservative Fields, Potential Functions
and Path Independence
If a function P(x, y) is a "nice" function, its gradient
field P(x, y) = Pxi + Pyj satisfy Pxy = Pyx since the
mixed partials are the same.
If a vector field F = fi + gj satisfy fy = gx and they are
continuous, then F is the gradient field of a "nice"
function P(x, y).
Example: a. Show the vector field
F(x, y) = xy2
i + (y + yx2
)j is conservative.
f(x, y) = xy2
, g(x, y) = y + yx2
fy = 2xy, gx = 2xy  fy = gx.

18. This theorem gives the converse of the above fact.
Conservative Fields, Potential Functions
and Path Independence
If a function P(x, y) is a "nice" function, its gradient
field P(x, y) = Pxi + Pyj satisfy Pxy = Pyx since the
mixed partials are the same.
If a vector field F = fi + gj satisfy fy = gx and they are
continuous, then F is the gradient field of a "nice"
function P(x, y).
Example: a. Show the vector field
F(x, y) = xy2
i + (y + yx2
)j is conservative.
f(x, y) = xy2
, g(x, y) = y + yx2
fy = 2xy, gx = 2xy  fy = gx.
Hence F(x, y) is conservative.

19. Conservative Fields, Potential Functions
and Path Independence
b. Find a potential function P(x, y) such that
P(x, y) = Pxi + Pyj = F(x, y) = xy2
i + (y + yx2
)j.

20. Conservative Fields, Potential Functions
and Path Independence
b. Find a potential function P(x, y) such that
P(x, y) = Pxi + Pyj = F(x, y) = xy2
i + (y + yx2
)j.
We recover the potential P(x, y) by partial integration.

21. Conservative Fields, Potential Functions
and Path Independence
b. Find a potential function P(x, y) such that
P(x, y) = Pxi + Pyj = F(x, y) = xy2
i + (y + yx2
)j.
We recover the potential P(x, y) by partial integration.
Since the gradient of P is to be F,
so Px = f(x, y) = xy2
.

22. Conservative Fields, Potential Functions
and Path Independence
b. Find a potential function P(x, y) such that
P(x, y) = Pxi + Pyj = F(x, y) = xy2
i + (y + yx2
)j.
We recover the potential P(x, y) by partial integration.
Since the gradient of P is to be F,
so Px = f(x, y) = xy2
.
Therefore P = ∫ f(x, y) dx = ∫ xy2
dx

23. Conservative Fields, Potential Functions
and Path Independence
b. Find a potential function P(x, y) such that
P(x, y) = Pxi + Pyj = F(x, y) = xy2
i + (y + yx2
)j.
We recover the potential P(x, y) by partial integration.
Since the gradient of P is to be F,
so Px = f(x, y) = xy2
.
Therefore P = ∫ f(x, y) dx = ∫ xy2
dx
treating y as a constant, we've
P = x2
y2
/2 + C(y)
where C(y) is a function in y and is to be determined.

24. Conservative Fields, Potential Functions
and Path Independence
b. Find a potential function P(x, y) such that
P(x, y) = Pxi + Pyj = F(x, y) = xy2
i + (y + yx2
)j.
We recover the potential P(x, y) by partial integration.
Since the gradient of P is to be F,
so Px = f(x, y) = xy2
.
But Py = g(x, y) = y + yx2
Therefore P = ∫ f(x, y) dx = ∫ xy2
dx
treating y as a constant, we've
P = x2
y2
/2 + C(y)
where C(y) is a function in y and is to be determined.

25. Conservative Fields, Potential Functions
and Path Independence
b. Find a potential function P(x, y) such that
P(x, y) = Pxi + Pyj = F(x, y) = xy2
i + (y + yx2
)j.
We recover the potential P(x, y) by partial integration.
Since the gradient of P is to be F,
so Px = f(x, y) = xy2
.
But Py = g(x, y) = y + yx2
= x2
y + Cy(y)
Therefore P = ∫ f(x, y) dx = ∫ xy2
dx
treating y as a constant, we've
P = x2
y2
/2 + C(y)
where C(y) is a function in y and is to be determined.

26. Conservative Fields, Potential Functions
and Path Independence
b. Find a potential function P(x, y) such that
P(x, y) = Pxi + Pyj = F(x, y) = xy2
i + (y + yx2
)j.
We recover the potential P(x, y) by partial integration.
Since the gradient of P is to be F,
so Px = f(x, y) = xy2
.
But Py = g(x, y) = y + yx2
= x2
y + Cy(y)  Cy(y) = y
Therefore P = ∫ f(x, y) dx = ∫ xy2
dx
treating y as a constant, we've
P = x2
y2
/2 + C(y)
where C(y) is a function in y and is to be determined.

27. Conservative Fields, Potential Functions
and Path Independence
b. Find a potential function P(x, y) such that
P(x, y) = Pxi + Pyj = F(x, y) = xy2
i + (y + yx2
)j.
We recover the potential P(x, y) by partial integration.
Since the gradient of P is to be F,
so Px = f(x, y) = xy2
.
But Py = g(x, y) = y + yx2
= x2
y + Cy(y)  Cy(y) = y
Hence C(y) = ∫ydy = y2
/2 + K
Therefore P = ∫ f(x, y) dx = ∫ xy2
dx
treating y as a constant, we've
P = x2
y2
/2 + C(y)
where C(y) is a function in y and is to be determined.

28. Conservative Fields, Potential Functions
and Path Independence
b. Find a potential function P(x, y) such that
P(x, y) = Pxi + Pyj = F(x, y) = xy2
i + (y + yx2
)j.
We recover the potential P(x, y) by partial integration.
Since the gradient of P is to be F,
so Px = f(x, y) = xy2
.
But Py = g(x, y) = y + yx2
= x2
y + Cy(y)  Cy(y) = y
Hence C(y) = ∫ydy = y2
/2 + K
Therefore P = ∫ f(x, y) dx = ∫ xy2
dx
treating y as a constant, we've
P = x2
y2
/2 + C(y)
where C(y) is a function in y and is to be determined.
So P(x, y) = x2
y2
/2 + y2
/2 + K

29. Fundemental Theorem of Line Integral
Conservative Fields, Potential Functions
and Path Independence

30. Fundemental Theorem of Line Integral
Given a conservative field F in a open simply
connected domain D and let P(x, y) be a potential
function of F .
Conservative Fields, Potential Functions
and Path Independence

31. Fundemental Theorem of Line Integral
Given a conservative field F in a open simply
connected domain D and let P(x, y) be a potential
function of F . Let (x0, y0) and (x1, y1) be two points in
D and C be any continuous curve from (x0, y0) to
(x1, y1).
Conservative Fields, Potential Functions
and Path Independence

32. Fundemental Theorem of Line Integral
Given a conservative field F in a open simply
connected domain D and let P(x, y) be a potential
function of F . Let (x0, y0) and (x1, y1) be two points in
D and C be any continuous curve from (x0, y0) to
(x1, y1).
Conservative Fields, Potential Functions
and Path Independence
(x0, y0)
(x1, y1)C

33. Fundemental Theorem of Line Integral
Given a conservative field F in a open simply
connected domain D and let P(x, y) be a potential
function of F . Let (x0, y0) and (x1, y1) be two points in
D and C be any continuous curve from (x0, y0) to
(x1, y1). Then the line integral
Conservative Fields, Potential Functions
and Path Independence
∫C
F • dC = P(x1, y1) – P(x0, y0)
(x0, y0)
(x1, y1)C

34. Fundemental Theorem of Line Integral
Given a conservative field F in a open simply
connected domain D and let P(x, y) be a potential
function of F . Let (x0, y0) and (x1, y1) be two points in
D and C be any continuous curve from (x0, y0) to
(x1, y1). Then the line integral
Conservative Fields, Potential Functions
and Path Independence
∫C
F • dC = P(x1, y1) – P(x0, y0)
(x0, y0)
(x1, y1)C1
C2
C3
From the theorem, the line
integrals in the figure
∫C1
F • dC = ∫C2
F • dC = ∫C3
F • dC
are the same in a conservative field F.

35. Conservative Fields, Potential Functions
and Path Independence
c. Use the fact that P(x, y) = x2
y2
/2 + y2
/2 + k is the
potential function of F(x, y) = xy2
i + (y + yx2
)j.
Find where
C = <cos(t), sin(t)> with
π/2 < t < π .
∫C
F • dC

36. Conservative Fields, Potential Functions
and Path Independence
c. Use the fact that P(x, y) = x2
y2
/2 + y2
/2 + k is the
potential function of F(x, y) = xy2
i + (y + yx2
)j.
Find where
C = <cos(t), sin(t)> with
π/2 < t < π .
∫C
F • dC
C (0, 1)
(-1, 0)

37. Conservative Fields, Potential Functions
and Path Independence
c. Use the fact that P(x, y) = x2
y2
/2 + y2
/2 + k is the
potential function of F(x, y) = xy2
i + (y + yx2
)j.
Find where
C = <cos(t), sin(t)> with
π/2 < t < π .
∫C
F • dC
Since F is conservative with potential P and
C(π/2) = (0, 1), C(π) = (-1, 0) as the starting and
ending points in the domain,
C (0, 1)
(-1, 0)

38. Conservative Fields, Potential Functions
and Path Independence
c. Use the fact that P(x, y) = x2
y2
/2 + y2
/2 + k is the
potential function of F(x, y) = xy2
i + (y + yx2
)j.
Find where
C = <cos(t), sin(t)> with
π/2 < t < π .
∫C
F • dC
Since F is conservative with potential P and
C(π/2) = (0, 1), C(π) = (-1, 0) as the starting and
ending points in the domain, therefore
∫C
F • dC = P(-1, 0) – P(0, 1)
C (0, 1)
(-1, 0)

39. Conservative Fields, Potential Functions
and Path Independence
c. Use the fact that P(x, y) = x2
y2
/2 + y2
/2 + k is the
potential function of F(x, y) = xy2
i + (y + yx2
)j.
Find where
C = <cos(t), sin(t)> with
π/2 < t < π .
∫C
F • dC
Since F is conservative with potential P and
C(π/2) = (0, 1), C(π) = (-1, 0) as the starting and
ending points in the domain, therefore
∫C
F • dC = P(-1, 0) – P(0, 1) = 0 – ½
C (0, 1)
(-1, 0)

40. Conservative Fields, Potential Functions
and Path Independence
c. Use the fact that P(x, y) = x2
y2
/2 + y2
/2 + k is the
potential function of F(x, y) = xy2
i + (y + yx2
)j.
Find where
C = <cos(t), sin(t)> with
π/2 < t < π .
∫C
F • dC
Since F is conservative with potential P and
C(π/2) = (0, 1), C(π) = (-1, 0) as the starting and
ending points in the domain, therefore
∫C
F • dC = P(-1, 0) – P(0, 1) = 0 – ½ = -1/2.
C (0, 1)
(-1, 0)

41. Corrolary: Given a conservative field F over an open
simply connected region D and C is a closed loop in
D, then
Conservative Fields, Potential Functions
and Path Independence
∫C
F • dC = 0

42. Corrolary: Given a conservative field F over an open
simply connected region D and C is a closed loop in
D, then
Conservative Fields, Potential Functions
and Path Independence
∫C
F • dC = 0
C
D

43. Corrolary: Given a conservative field F over an open
simply connected region D and C is a closed loop in
D, then
Conservative Fields, Potential Functions
and Path Independence
∫C
F • dC = 0
(x0, y0)
=(x1, y1)
Proof: A closed loop is just a curve with the starting
point the same as the ending point.
C
D

44. Corrolary: Given a conservative field F over an open
simply connected region D and C is a closed loop in
D, then
Conservative Fields, Potential Functions
and Path Independence
∫C
F • dC = 0
(x0, y0)
=(x1, y1)
Proof: A closed loop is just a curve with the starting
point the same as the ending point.
F is conservative so it has a
potential function P(x, y) and
∫C
F • dC = P(x0, y0) – P(x1 – y1)
C
D

45. Corrolary: Given a conservative field F over an open
simply connected region D and C is a closed loop in
D, then
Conservative Fields, Potential Functions
and Path Independence
∫C
F • dC = 0
(x0, y0)
=(x1, y1)
Proof: A closed loop is just a curve with the starting
point the same as the ending point.
F is conservative so it has a
potential function P(x, y) and
∫C
F • dC = P(x0, y0) – P(x1 – y1)
= 0.
as shown.
C
D