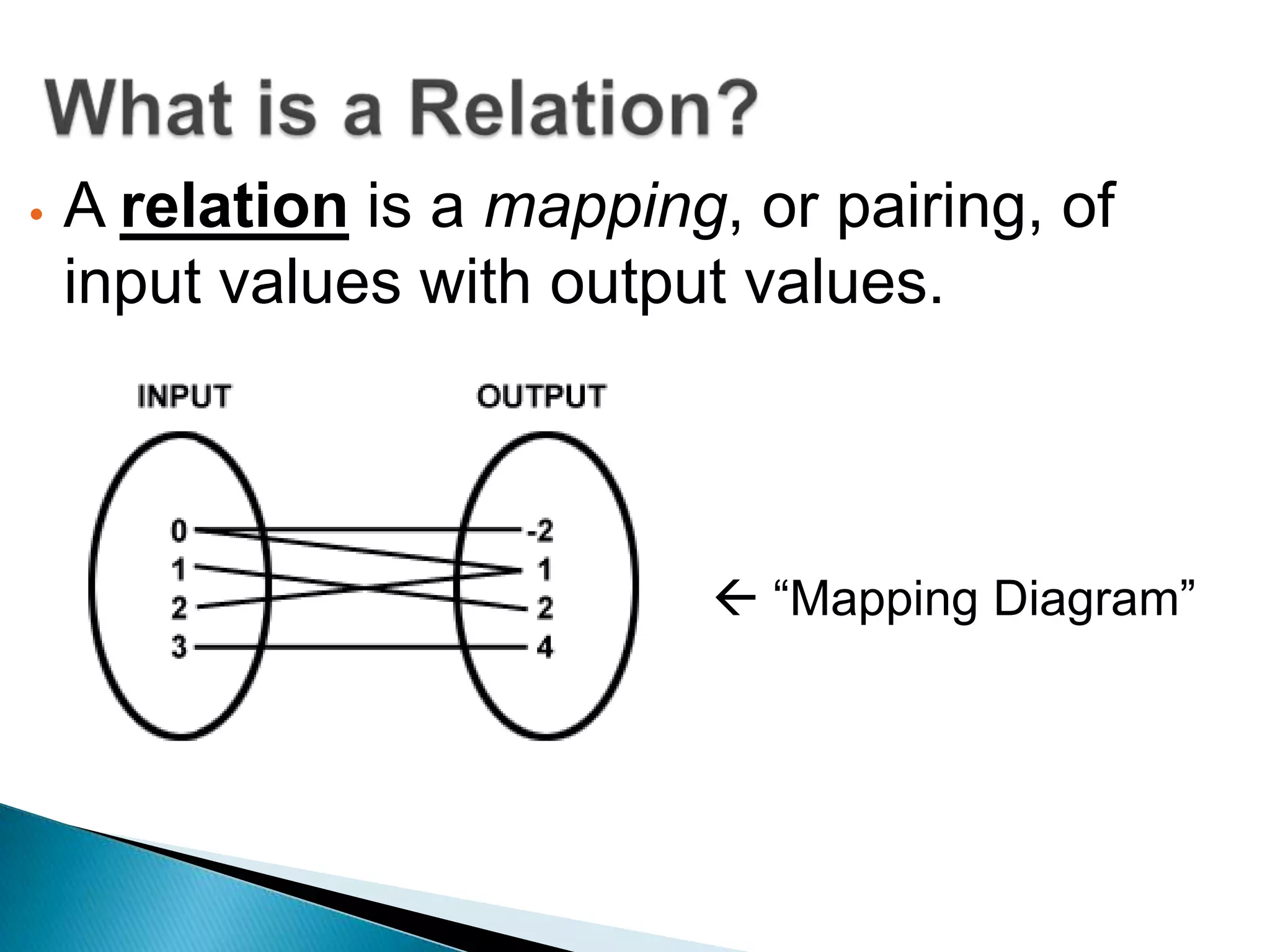
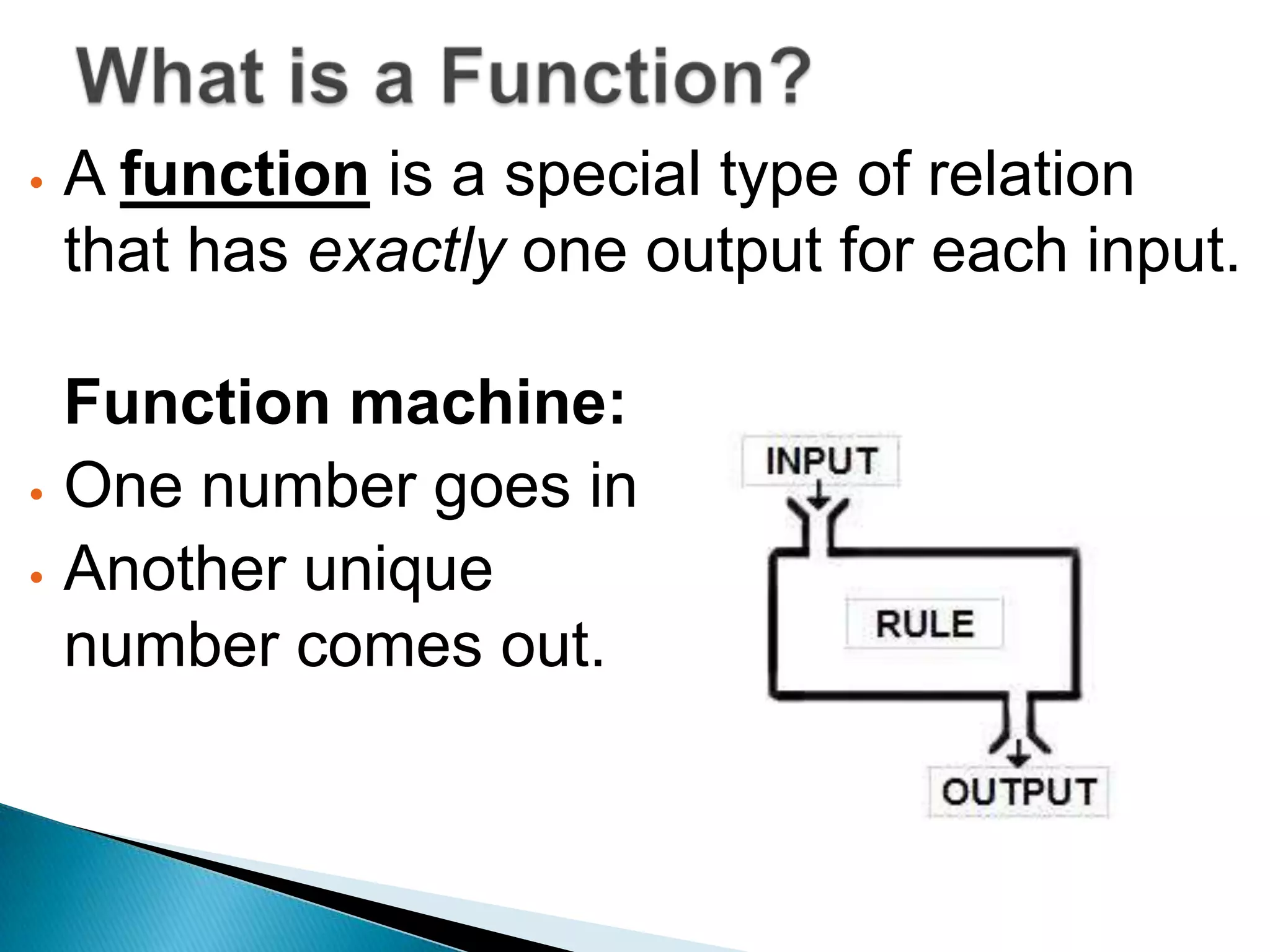
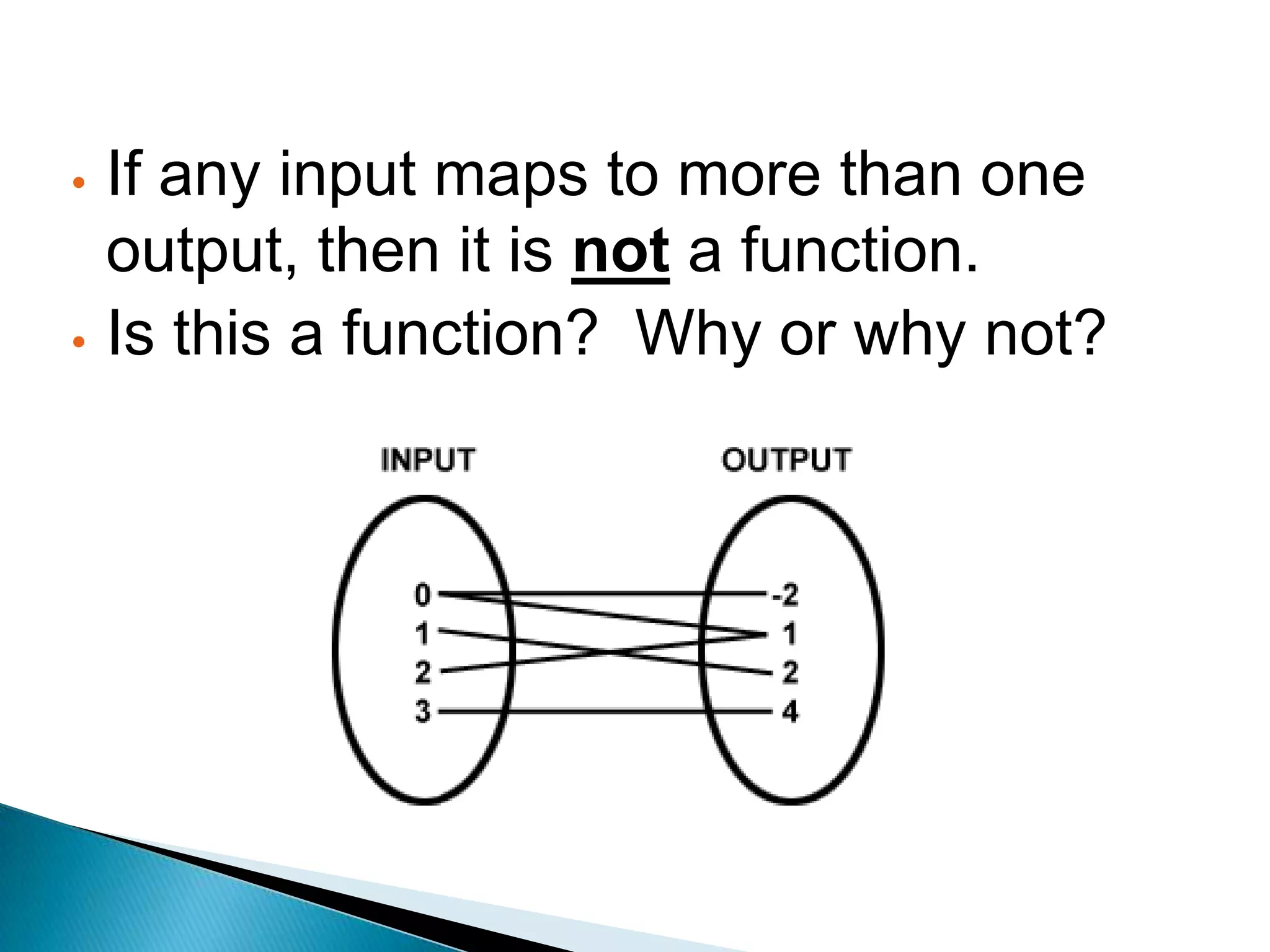
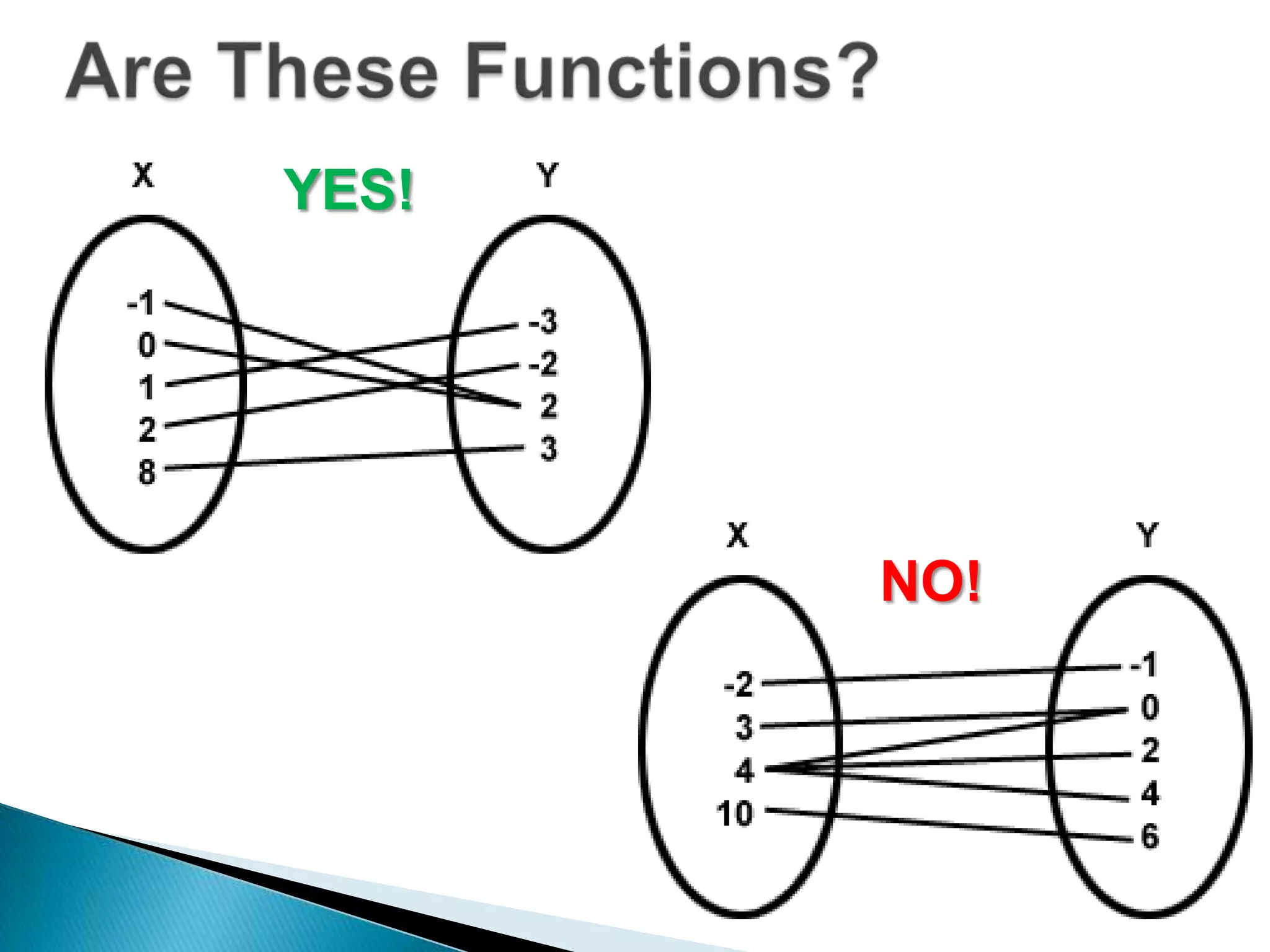
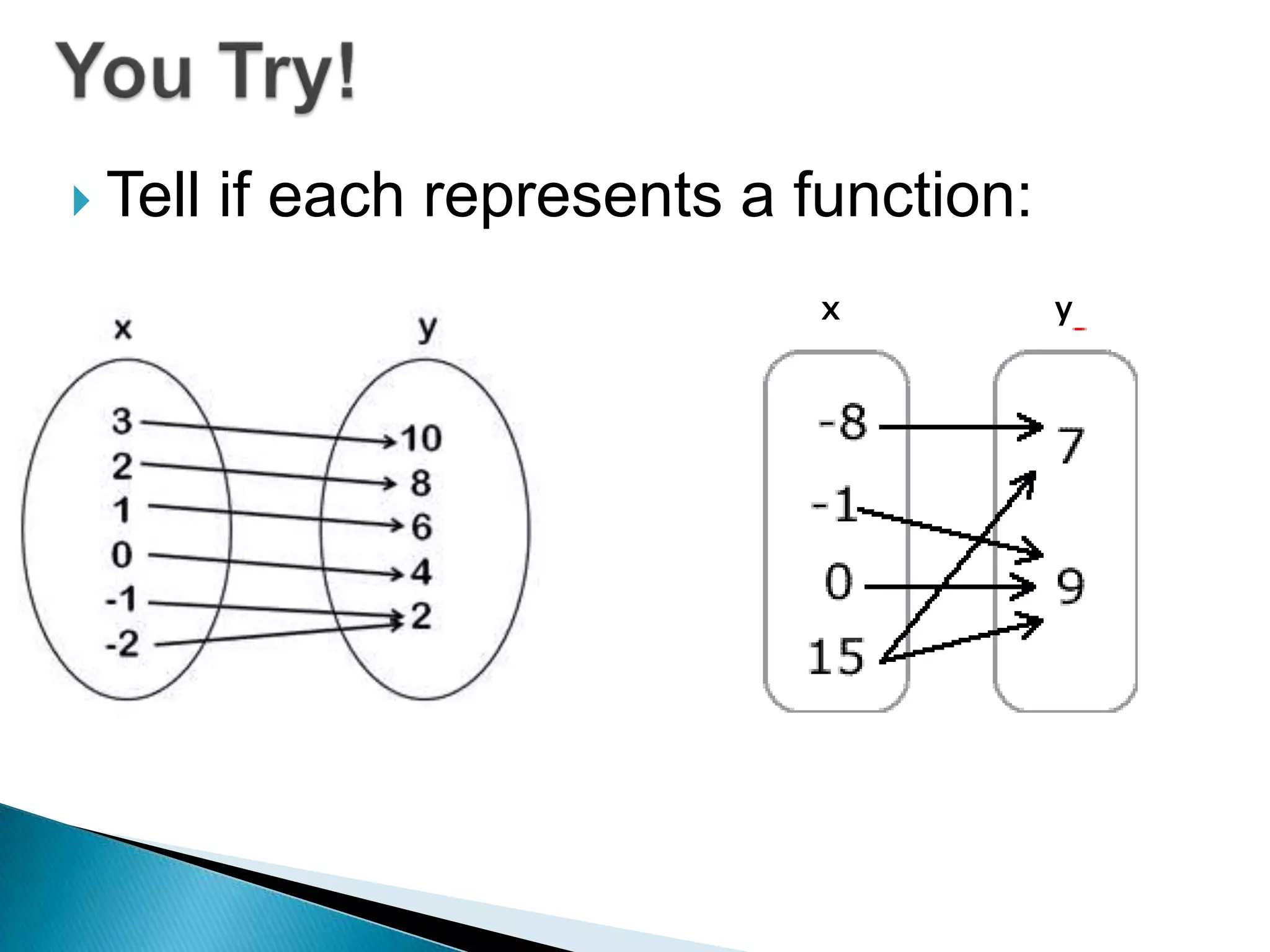
- A relation maps inputs to outputs, while a function is a special type of relation that maps each input to a single, unique output. - A relation qualifies as a function only if each input maps to exactly one output, and no input maps to multiple outputs. - Relations and functions can be represented using ordered pairs in a table, graphically with a graph, or with an equation.

2. • A relation is a mapping, or pairing, of
input values with output values.
 “Mapping Diagram”

3. • A function is a special type of relation
that has exactly one output for each input.
Function machine:
• One number goes in
• Another unique
number comes out.

4. • If any input maps to more than one
output, then it is not a function.
• Is this a function? Why or why not?

5.  Most functions we will see use x and y
to represent inputs and outputs.
 x = input value
 y = output value

6. YES!
NO!

7.  Tell if each represents a function:
x y

8.  Relations and functions can also be
represented using:
 a set of ordered pairs
 a table
 a graph
 an equation
We’ll study these later!

9.  Is the relation a function?
 Remember: each input (x) can only
have one unique output (y)
 {(0, 2), (1, 2), (3, 1), (4, 5)}
 {(-2, 4), (0, 3), (-2, 2), (-4, 1)}
YES!
NO!

10.  Determine whether the relation is a
function:
 {(2, 6), (3, 7), (4, 8), (3, 9)}
 {(1, -3), (0, -4), (-1, -3), (-2, -2)}

11. • A graph is a function
if and only if no vertical
line crosses the graph
at more than one point.

12.  Determine whether each graph
represents a function.
YES! YES! NO!

13.  Determine whether each graph
represents a function.