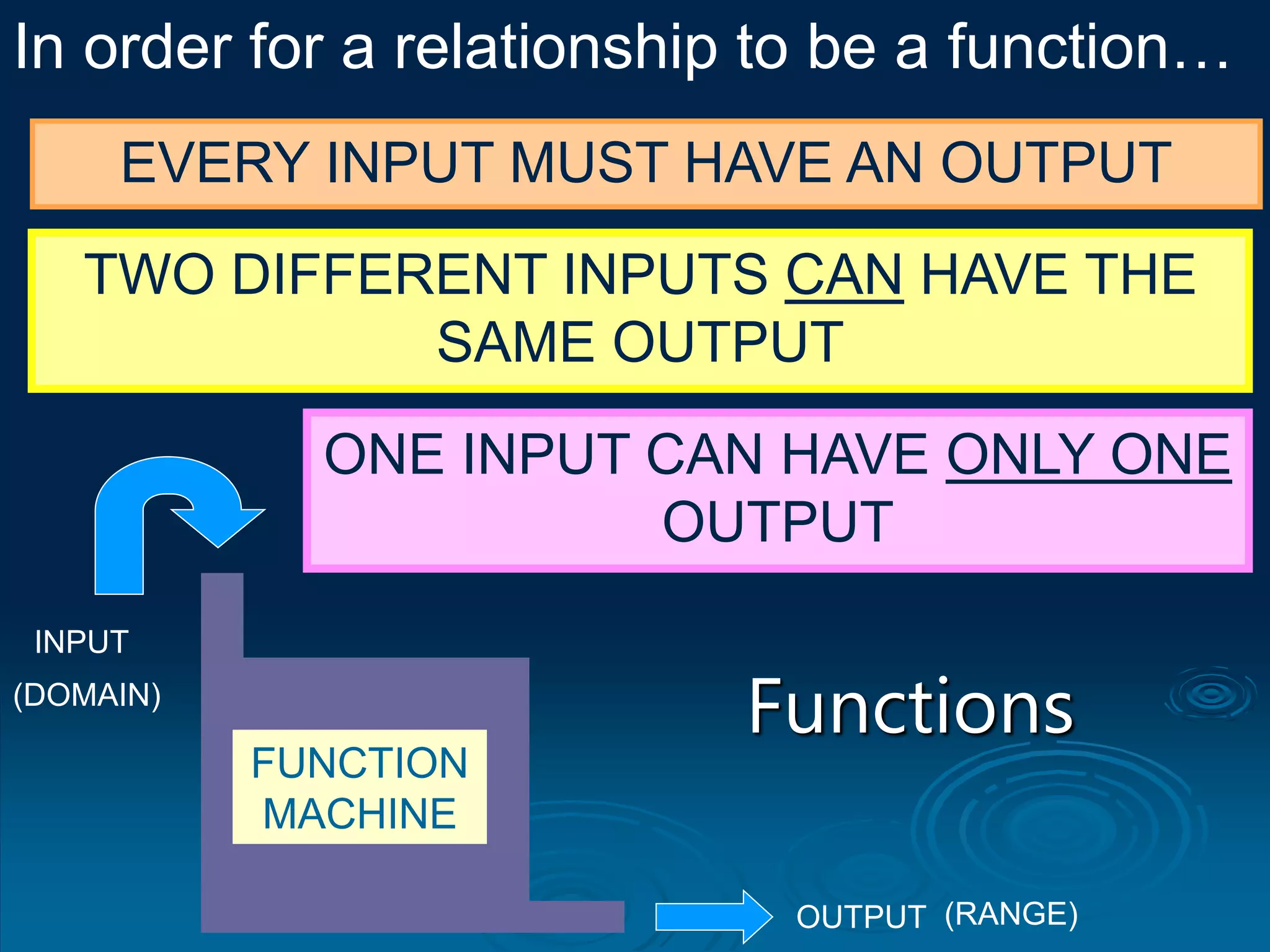
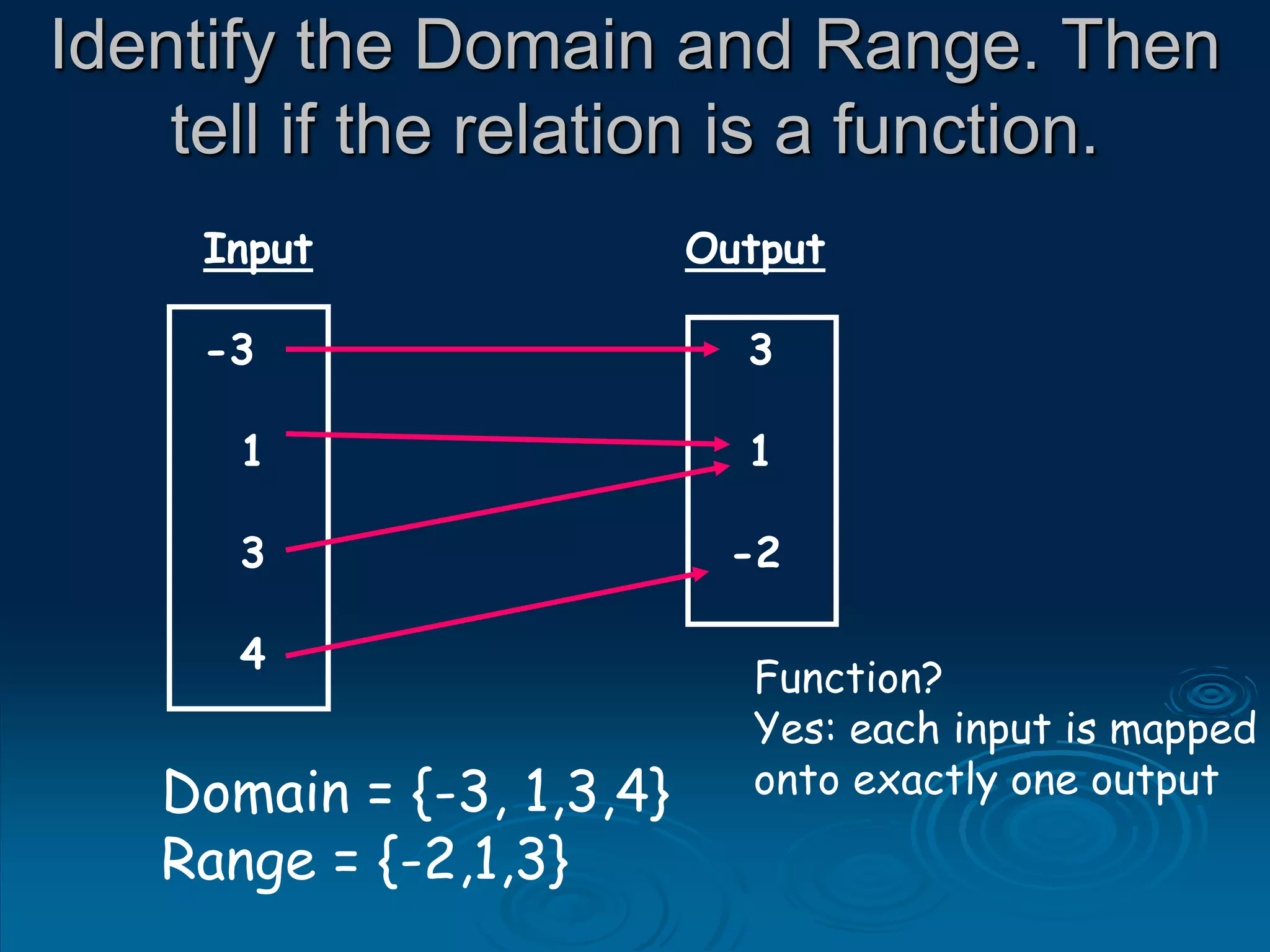
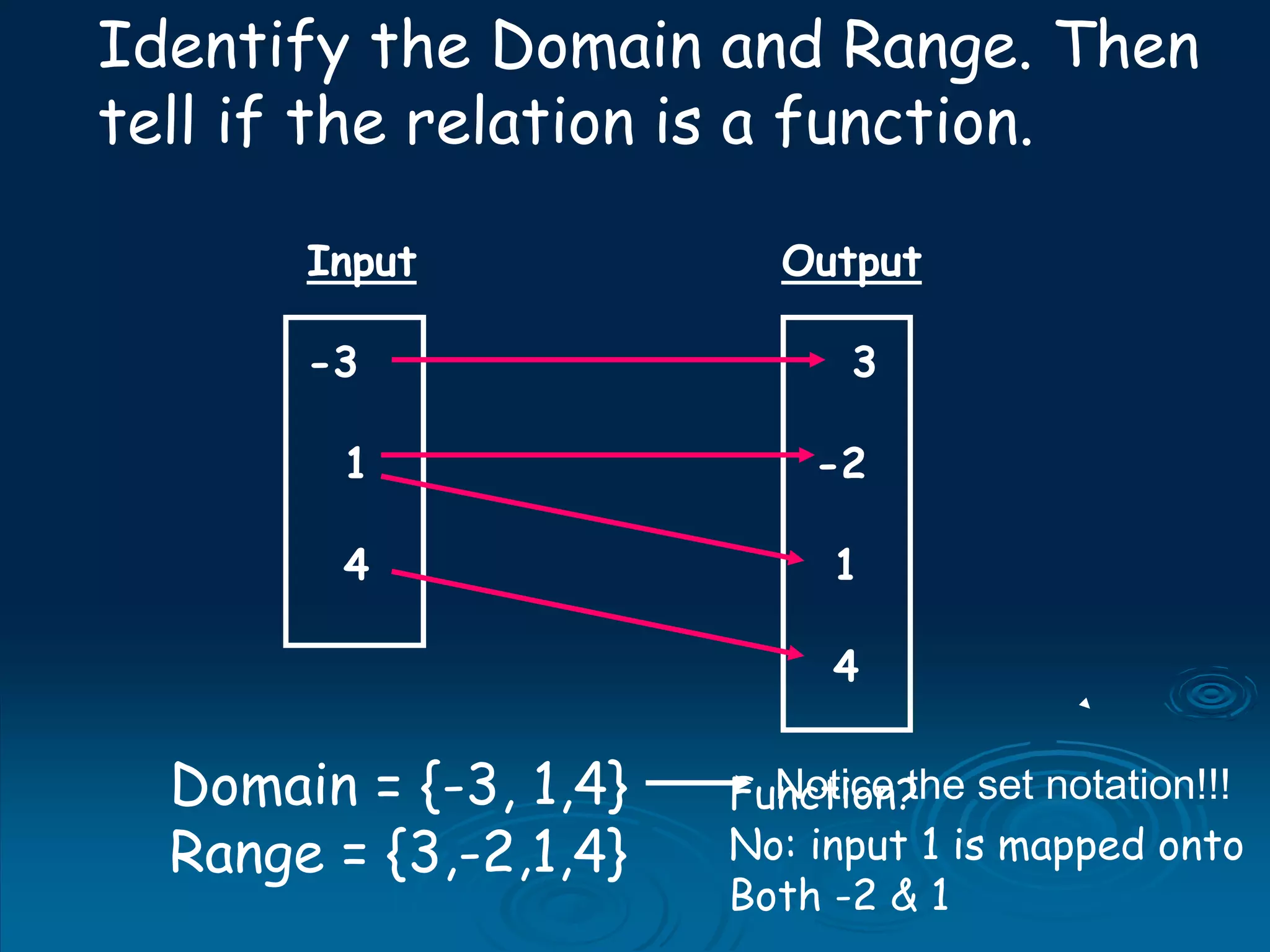
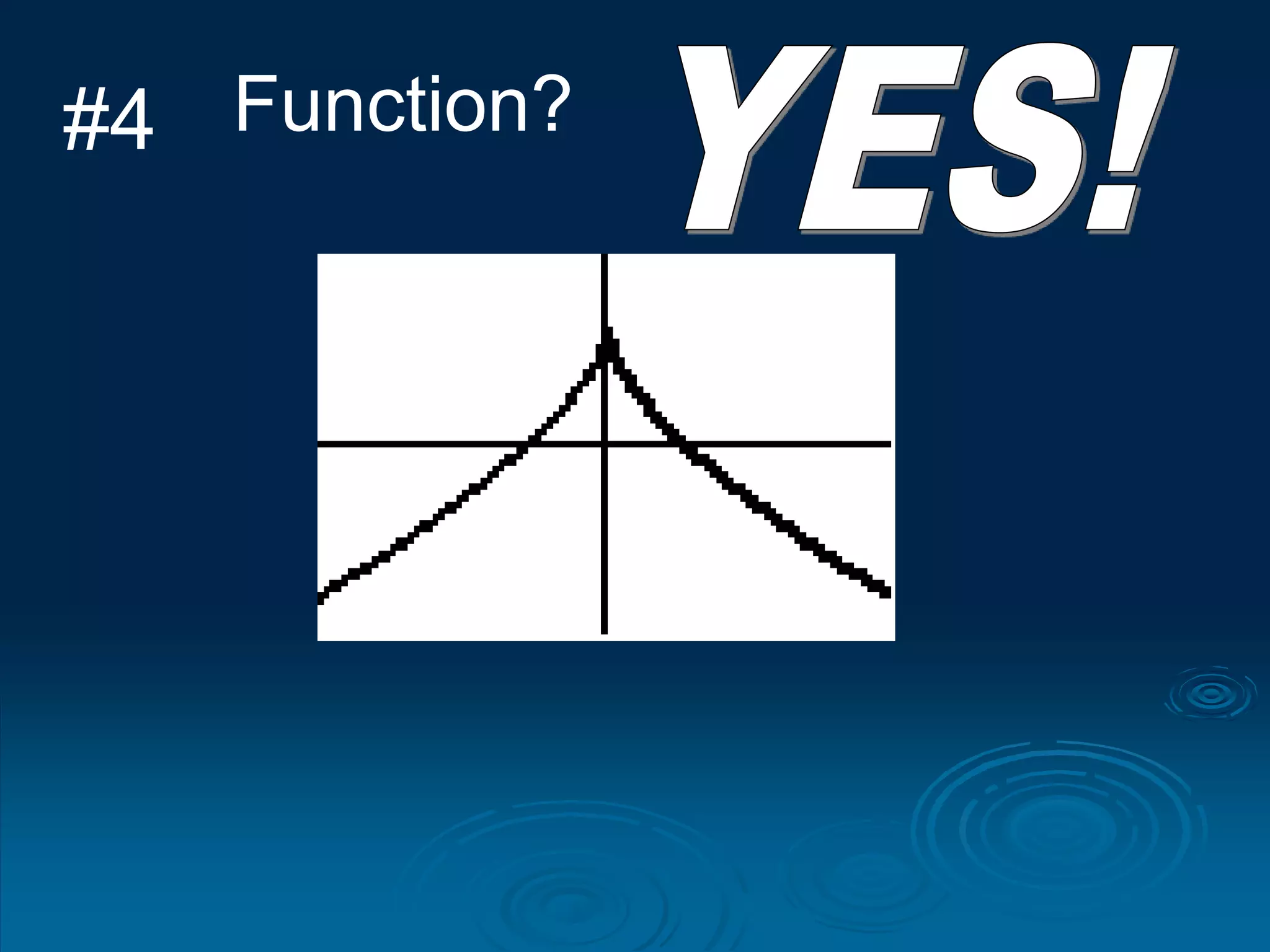
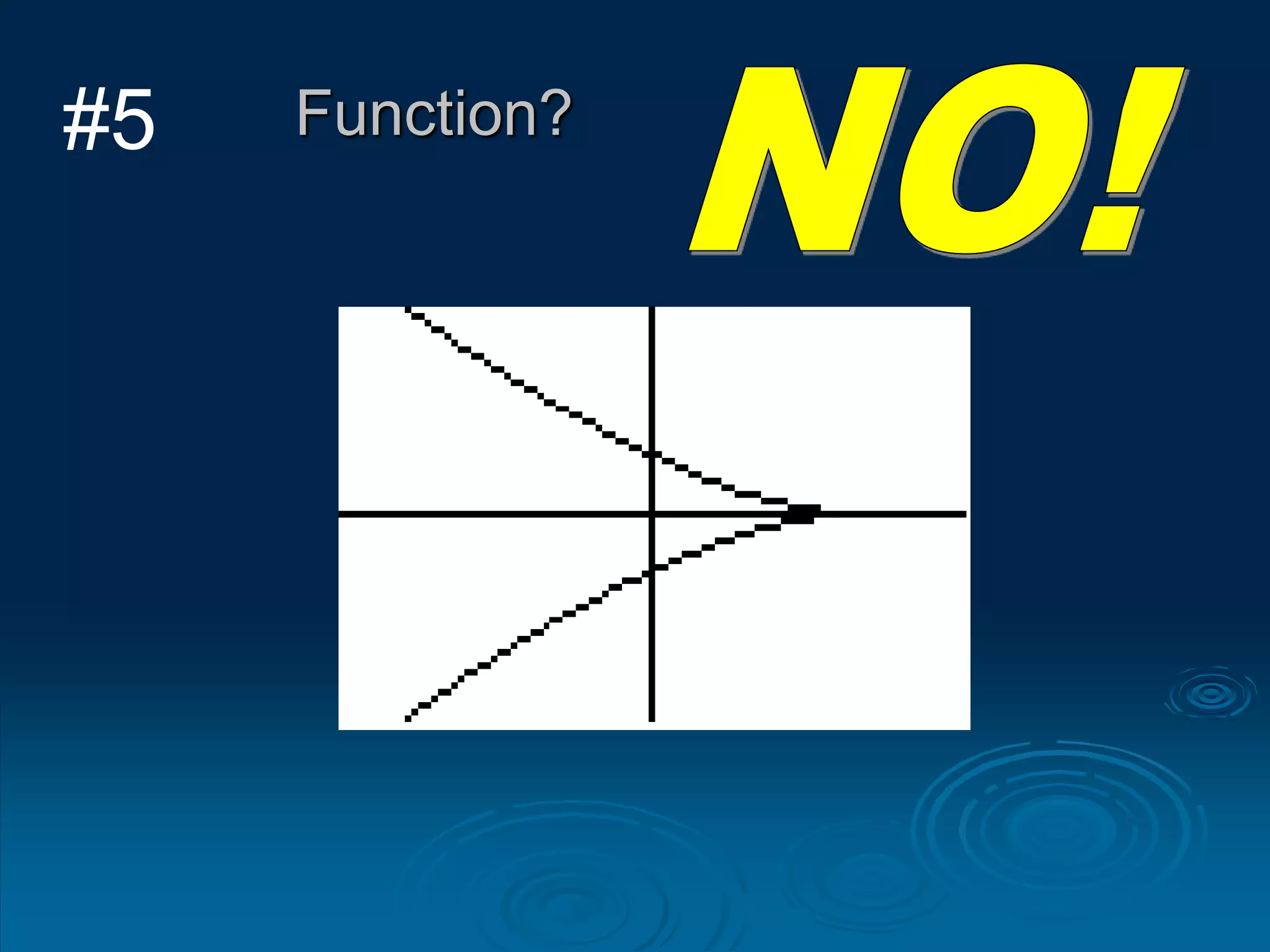
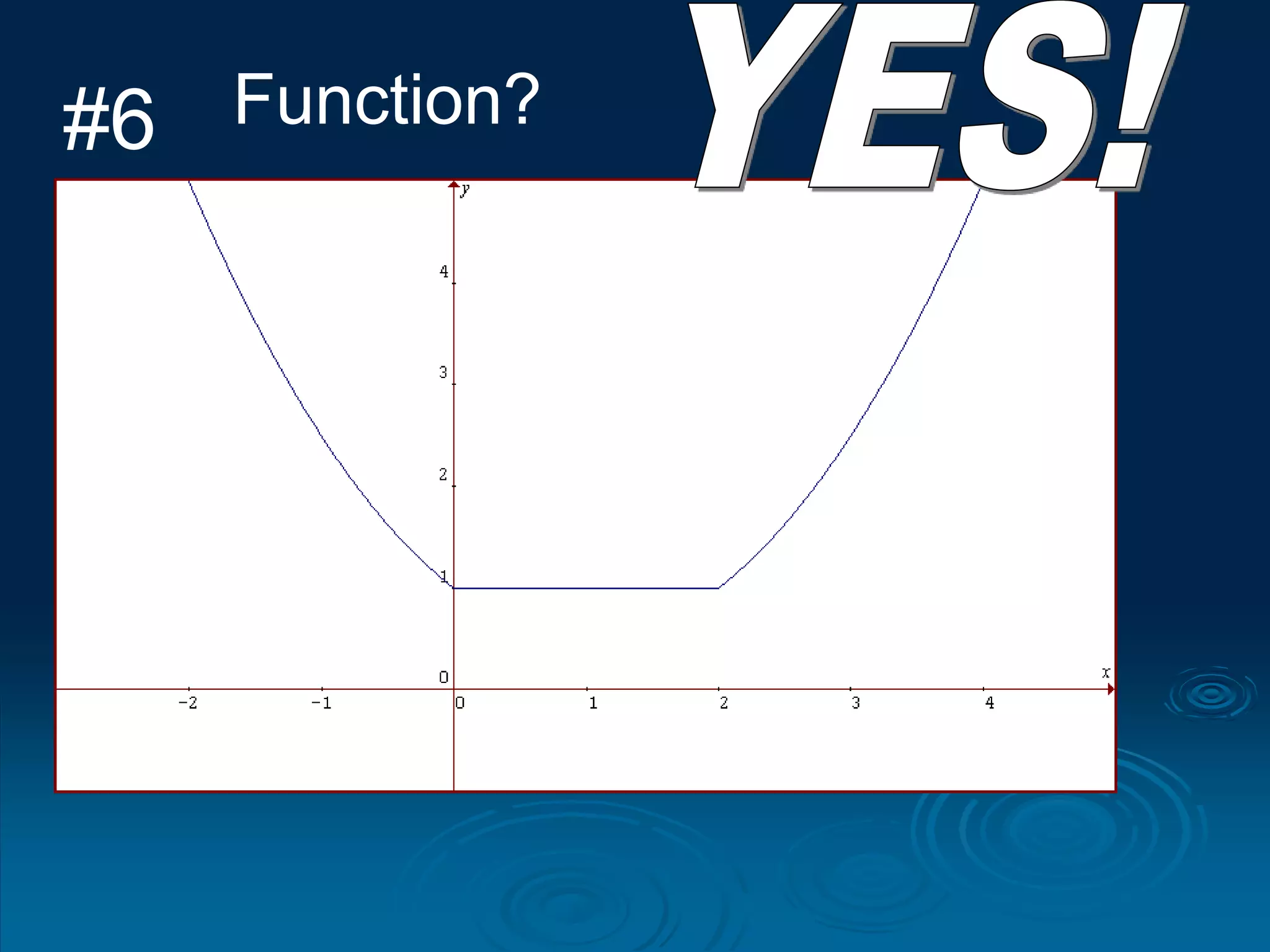
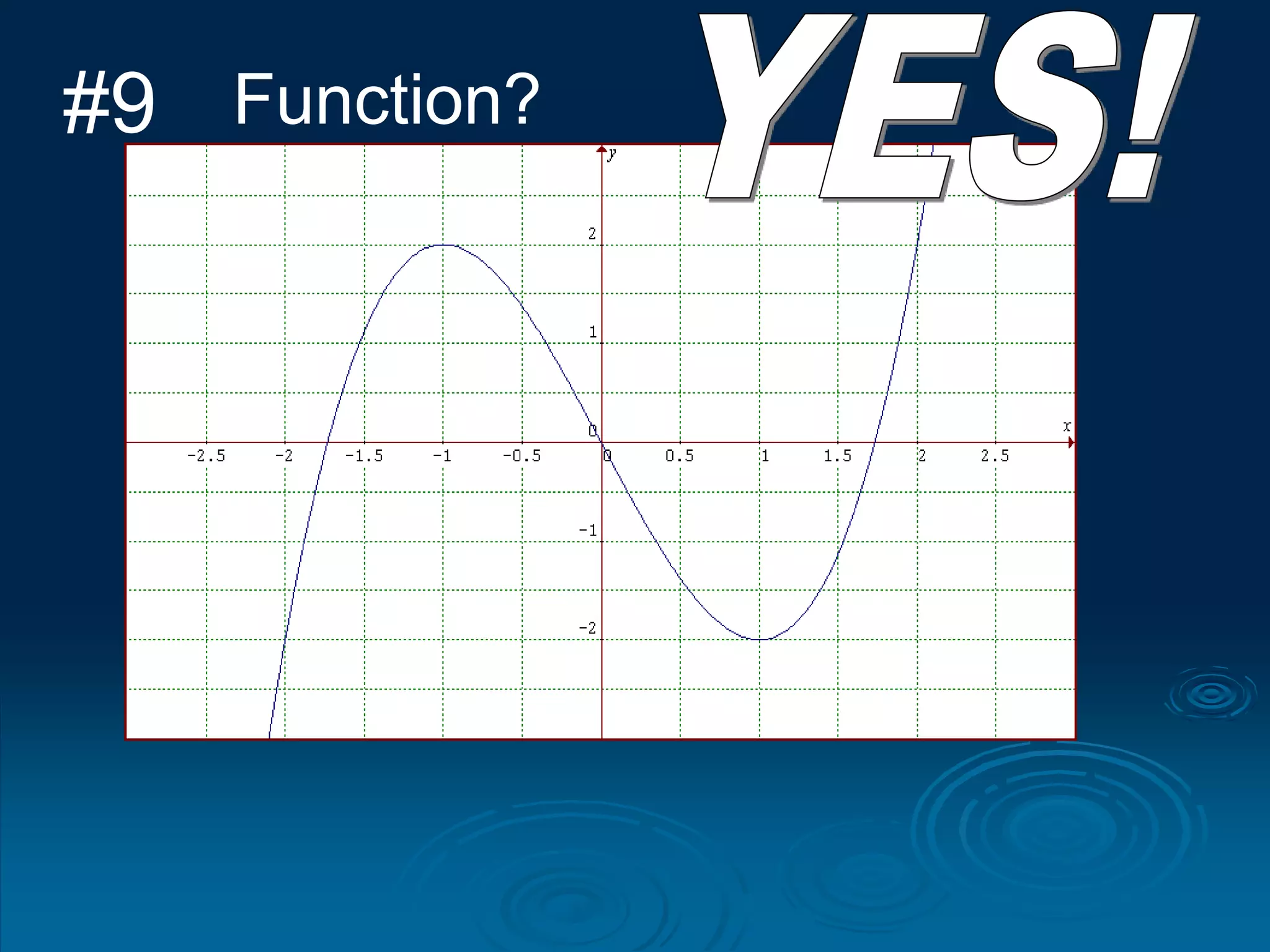
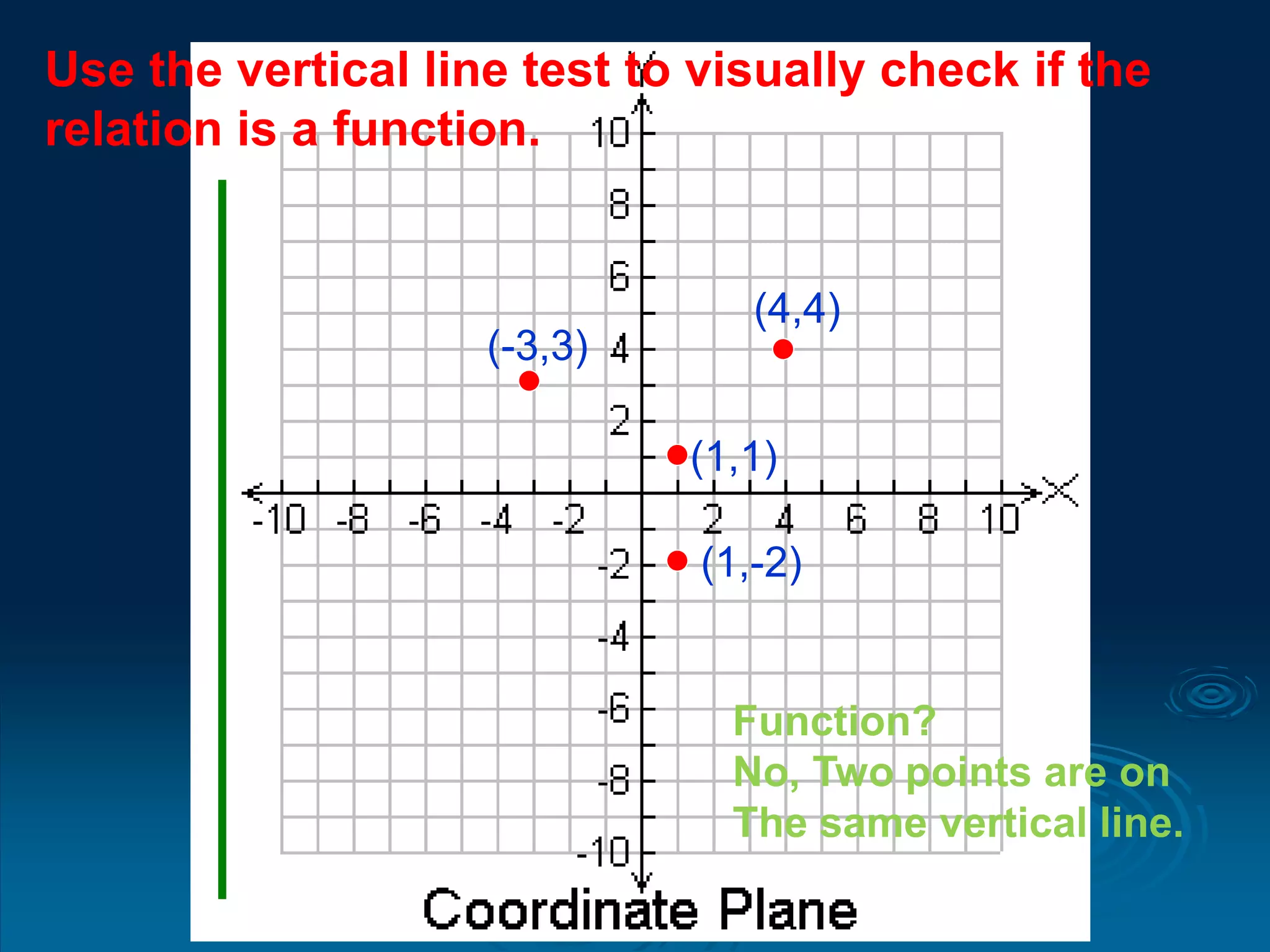
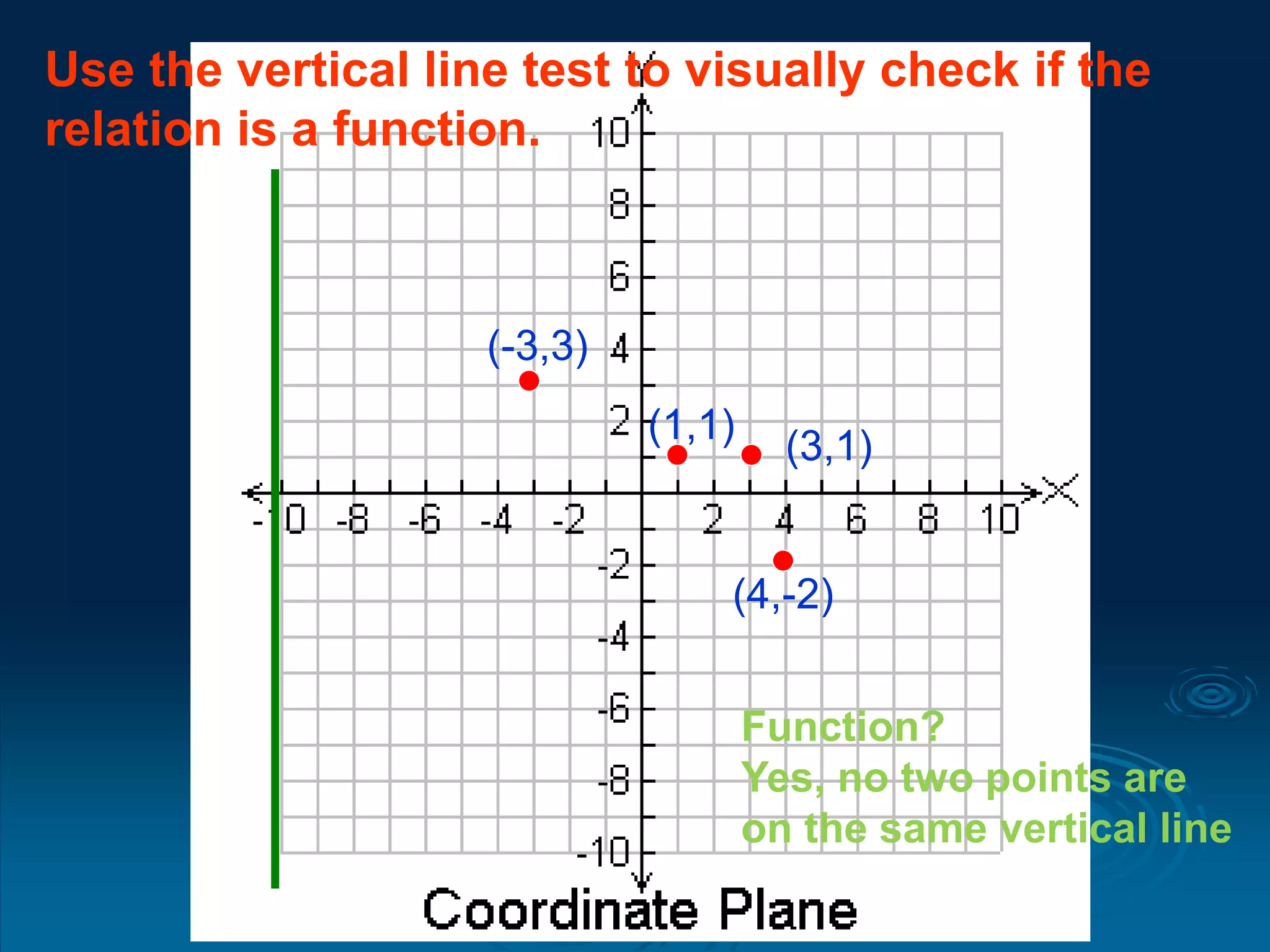
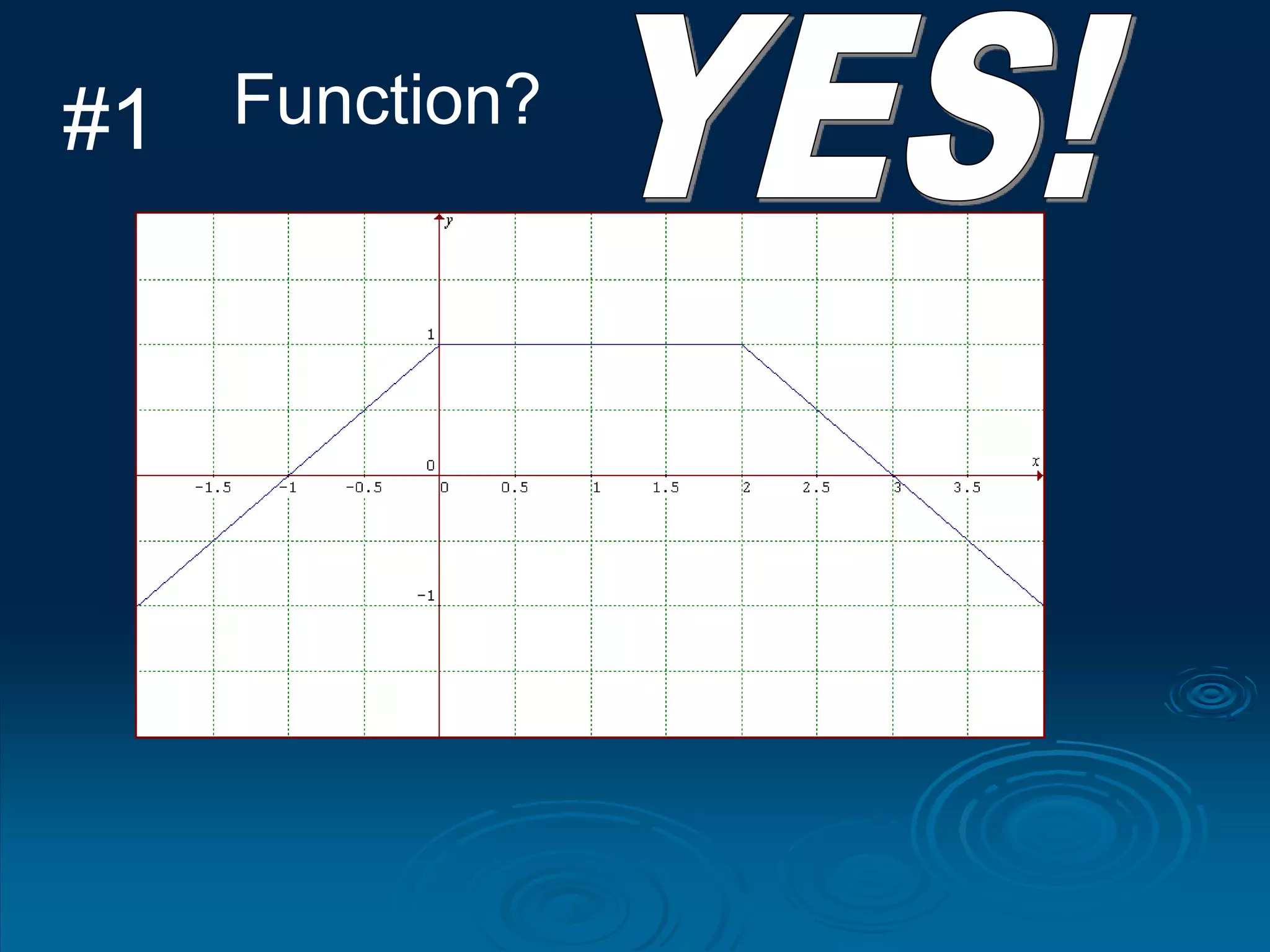
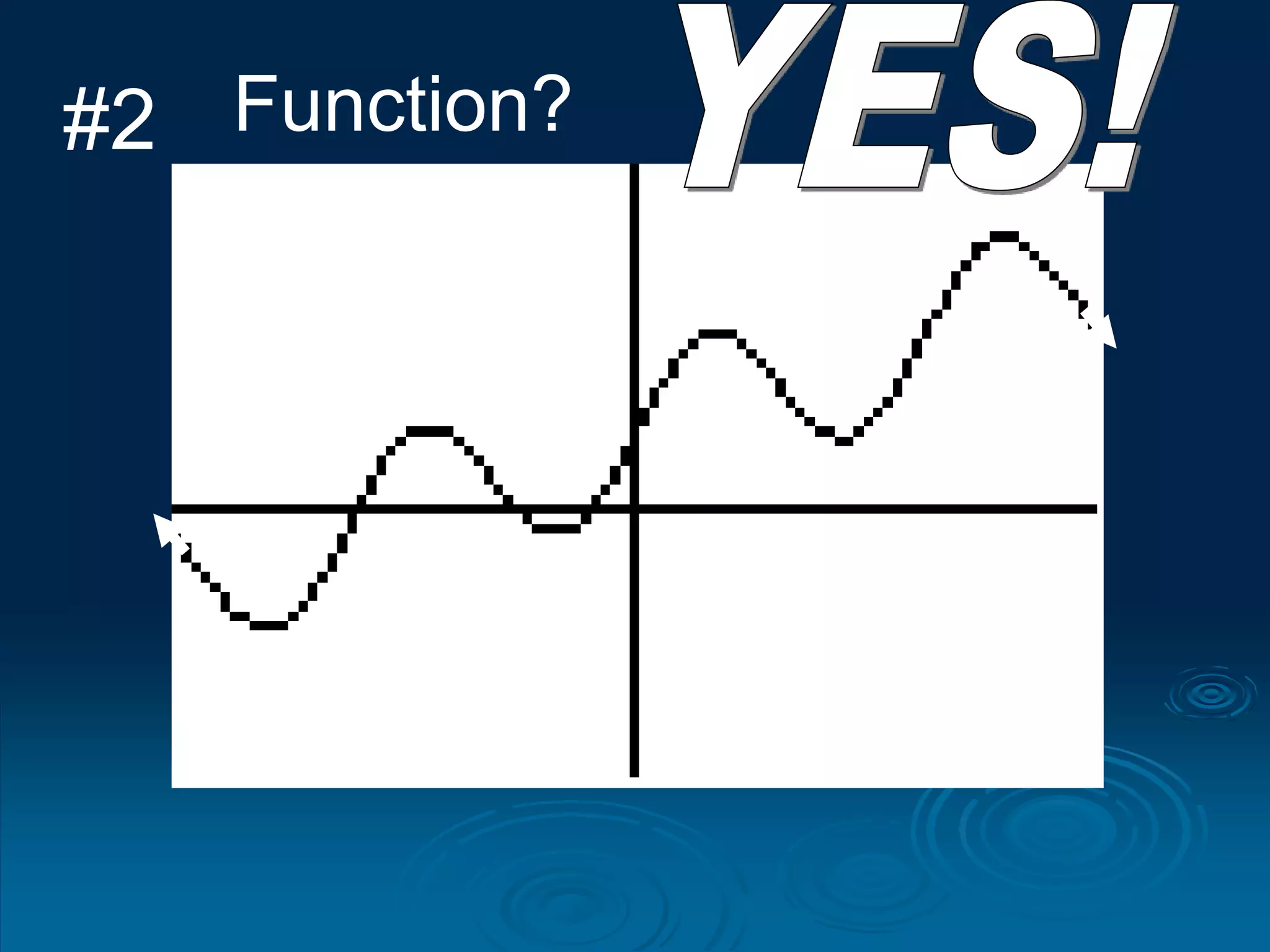
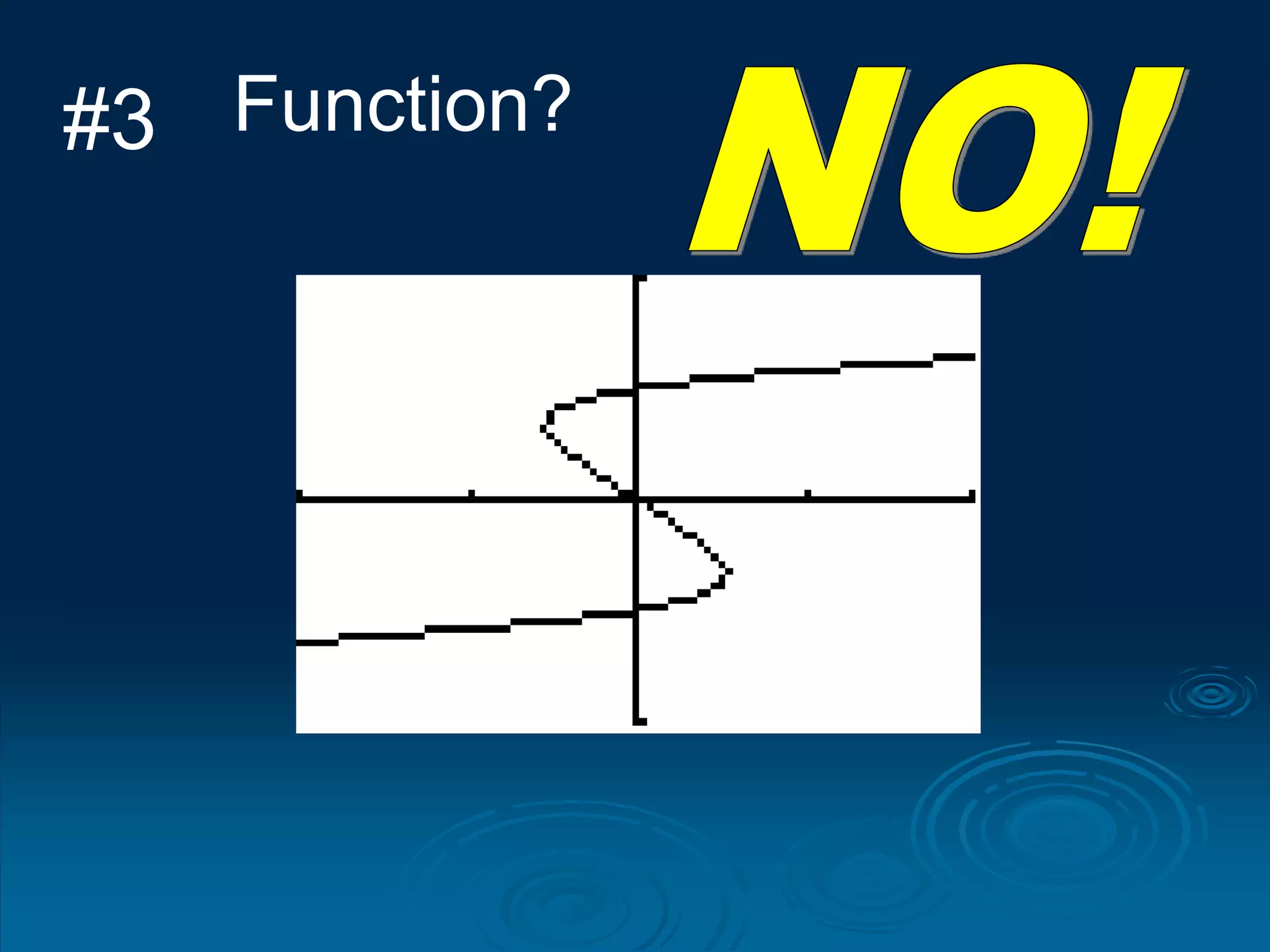
1. A function is a relation where each input is mapped to exactly one output. It is not a function if one input has more than one output. 2. For a relation to be a function, every input must have an output and two different inputs cannot have the same output. One input can only have one output. 3. The vertical line test can be used to visually check if a relation is a function - if any vertical line intersects the graph at more than one point, it is not a function.

1. 4-3 Functions
•A relation is a function provided there is exactly
one output for each input.
•It is NOT a function if one input has more than
one output

2. INPUT
(DOMAIN)
OUTPUT (RANGE)
FUNCTION
MACHINE
In order for a relationship to be a function…
EVERY INPUT MUST HAVE AN OUTPUT
TWO DIFFERENT INPUTS CAN HAVE THE
SAME OUTPUT
Functions
ONE INPUT CAN HAVE ONLY ONE
OUTPUT

3. Example 6
No two ordered pairs can have the
same first coordinate
(and different second coordinates).
Which of the following relations are
functions?
R= {(9,10), (-5, -2), (2, -1), (3, -9)}
S= {(6, a), (8, f), (6, b), (-2, p)}
T= {(z, 7), (y, -5), (r, 7), (z, 0), (k, 0)}

4. Identify the Domain and Range. Then
tell if the relation is a function.
Input Output
-3 3
1 1
3 -2
4
Domain = {-3, 1,3,4}
Range = {-2,1,3}
Function?
Yes: each input is mapped
onto exactly one output

5. Input Output
-3 3
1 -2
4 1
4
Identify the Domain and Range. Then
tell if the relation is a function.
Domain = {-3, 1,4}
Range = {3,-2,1,4}
Function?
No: input 1 is mapped onto
Both -2 & 1
Notice the set notation!!!

6. 1. {(2,5) , (3,8) , (4,6) , (7, 20)}
2. {(1,4) , (1,5) , (2,3) , (9, 28)}
3. {(1,0) , (4,0) , (9,0) , (21, 0)}

7. The Vertical Line Test
If it is possible for a vertical line
to intersect a graph at more
than one point, then the graph
is NOT the graph of a function.
Page 117

8. (-3,3)
(4,4)
(1,1)
(1,-2)
Function?
No, Two points are on
The same vertical line.
Use the vertical line test to visually check if the
relation is a function.

9. (-3,3)
(4,-2)
(1,1)
(3,1)
Use the vertical line test to visually check if the
relation is a function.
Function?
Yes, no two points are
on the same vertical line

10. Examples
I’m going to show you a series of
graphs. **don’t write 
Determine whether or not these
graphs are functions.
You do not need to draw the graphs in
your notes. **or write this note

11. #1 Function?

12. Function?
#2

13. Function?
#3

14. Function?
#4

15. Function?
#5

16. #6 Function?

17. Function?
#7

18. Function?
#8

19. #9 Function?

20. )
(x
f
“f of x”
Input = x
Output = f(x) = y
Function Notation

21. y = 6 – 3x
-2
-1
0
1
2
12
9
6
0
3
x y
f(x) = 6 – 3x
-2
-1
0
1
2
12
9
6
0
3
x f(x)
Before… Now…
(x, y)
(input, output)
(x, f(x))

22. Example.
f(x) = 2x2 – 3
Find f(0), f(-3), f(5).

23. Finding the Domain of a
Function
 When a function is defined by an equation
and the domain of the function is not
stated, we assume that the domain is
All Real Numbers
 There will be certain cases where specific
numbers cannot be included in the domain
or a set of numbers cannot be included in
the domain

24. Examples…
 f(x) = 2x – 5
*there would be no restrictions on this, so the
domain is All Real Numbers
 g(x) = 1
x – 2
*a denominator cannot equal 0, so x ≠ 2.
The domain is {x | x ≠ 2}
 h(x) = √x + 6
*you cannot take the square root of a
negative number, so x must be ≥ -6. The domain
is {x | x ≥ -6}

25. Your Turn…Find the domain of
each function
 f(x) = x2 + 2
 g(x) = √x – 1
 h(x) = 1
x + 5