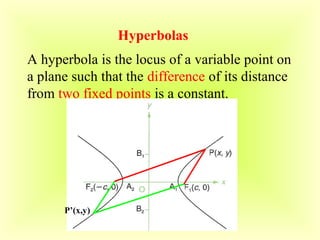
The document discusses the properties and definitions of conic sections: circles, ellipses, parabolas, and hyperbolas. It describes how each shape is formed based on the intersection of a plane with cones, providing equations and parameters related to their geometric properties. Additionally, it includes the general equations for tangents to conics and various forms of their standard equations.

1. Conics

2. Conic Sections
(1) Circle
A circle is formed when
i.e. when the plane Ω is
perpendicular to the
axis of the cones.
2
π
θ =

3. Conic Sections
(2) Ellipse
An ellipse is formed when
i.e. when the plane Ω cuts
only one of the cones, but
is neither perpendicular to
the axis nor parallel to the
a generator.
2
π
θα <<

4. Conic Sections
(3) Parabola
A parabola is formed when
i.e. when the plane Ω is
parallel to a generator.
αθ =

5. Conic Sections
(4) Hyperbola
A hyperbola is formed when
i.e. when the plane Ω cuts
both the cones, but does not
pass through the common
vertex.
αθ <≤0

6. Parabola
A parabola is the locus of a variable point on a
plane so that its distance from a fixed point
(the focus) is equal to its distance from a fixed
line (the directrix x = - a).
focus F(a,0)
P(x,y)
M(-a,0) x
y
O

7. Form the definition of parabola,
PF = PN
axyax +=+− 22
)(
222
)()( axyax +=+−
22222
22 aaxxyaaxx ++=++−
axy 42
=
standard equation of a parabola

8. mid-point of FM = the origin (O) = vertex
length of the latus rectum = LL’= 4a
vertex
latus rectum (LL’)
axis of symmetry

10. Other forms of Parabola
axy 42
−=

11. Other forms of Parabola
ayx 42
=

12. Other forms of Parabola
ayx 42
−=

13. Ellipses
An ellipse is the locus of a variable point on a
plane so that the sum of its distance from two
fixed points is a constant.
P’(x,y)
P’’(x,y)

14. Let PF1+PF2 = 2a where a > 0
aycxycx 2)()( 2222
=++++−
2222
)(2)( ycxaycx ++−=+−
222222
)()(44)( ycxycxaaycx +++++−=+−
222
44)(4 acxycxa +=++
42222222
2)2( acxaxcycxcxa ++=+++
42222222222
22 acxaxcyacaxcaxa ++=+++

15. 22422222
)( caayaxca −=+−
)()( 22222222
caayaxca −=+−
222
cabLet −=
222222
bayaxb =+
12
2
2
2
=+
b
y
a
x standard equation of
an ellipse

16. vertex
major axis = 2a
minor axis = 2b
lactus rectum
length of semi-major axis = a
length of the semi-minor axis = b
length of lactus rectum =
a
b2
2

18. Other form of Ellipse
12
2
2
2
=+
a
y
b
x

19. Hyperbolas
A hyperbola is the locus of a variable point on
a plane such that the difference of its distance
from two fixed points is a constant.
P’(x,y)

20. Let |PF1-PF2|= 2a where a > 0
aycxycx 2|)()(| 2222
=++−+−
2222
)(2)( ycxaycx +++±=+−
222222
)()(44)( ycxycxaaycx +++++±=+−
222
44)(4 acxycxa +=++
42222222
2)2( acxaxcycxcxa ++=+++
42222222222
22 acxaxcyacaxcaxa ++=+++

21. 42222222
)( acayaxac −=−−
)()( 22222222
acayaxac −=−−
222
acbLet −=
222222
bayaxb =−
12
2
2
2
=−
b
y
a
x standard equation of
a hyperbola

22. vertex
transverse axis
conjugate axis
lactus rectum
length of lactus rectum =
a
b2
2
length of the semi-transverse axis = a
length of the semi-conjugate axis = b

23. asymptote
x
a
b
y ±=equation of
asymptote :

24. Other form of Hyperbola :
12
2
2
2
=−
b
x
a
y

25. Rectangular Hyperbola
If b = a, then
222
ayx =−12
2
2
2
=−
b
y
a
x
12
2
2
2
=−
b
x
a
y 222
axy =−
The hyperbola is said to be rectangular
hyperbola.

26. equation of asymptote : 0=± yx

27. If the rectangular hyperbola x2
– y2
= a2
is
rotated through 45o
about the origin, then the
coordinate axes will become the asymptotes.
equation becomes :
2
2
a
xy =

28. Simple Parametric Equations and Locus Problems
x = f(t)
y = g(t)
parametric equations
parameter
Combine the two parametric equations into
one equation which is independent of t.
Then sketch the locus of the equation.

29. Equation of Tangents to
Conicsgeneral equation of conics :
022
=+++++ FEyDxCyBxyAx
Steps :
(1) Differentiate the implicit equation to find .
(2) Put the given contact point (x1,y1) into
to find out the slope of tangent at that point.
(3) Find the equation of the tangent at that point.
dx
dy
dx
dy

30. OR
0)(
2
)(
2
)(
2
111111 =+++++++++ Fyy
E
xx
D
yCyyxxy
B
Ax

31. Conics Parabola Ellipse Hyperbola
Graph
Definition PF = PN PF1 + PF2 = 2a | PF1 + PF2 | = 2a

32. Conics Parabola Ellipse Hyperbola
Graph
Standard
Equation axy 42
= 12
2
2
2
=+
b
y
a
x
12
2
2
2
=−
b
y
a
x

33. Conics Parabola Ellipse Hyperbola
Graph
Directrix x = -a
,
e
a
x = ,
e
a
x =
PN
PF
e 1
=
PN
PF
e 1
=

34. Conics Parabola Ellipse Hyperbola
Graph
Vertices (0,0) A1(a,0), A2(-a,0),
B1(0,b), B2(0,-b)
A1(a,0), A2(-
a,0)

35. Conics Parabola Ellipse Hyperbola
Graph
Axes axis of
parabola = the
x-axis
major axis = A1A2
minor axis =B1B2
transverse axis =A1A2
conjugate axis =B1B2
where B1(0,b), B2(0,-b)

36. Conics Parabola Ellipse Hyperbola
Graph
Length of
lantus
rectum LL’
4a
a
b2
2
a
b2
2

37. Conics Parabola Ellipse Hyperbola
Graph
Asymptotes ---- ----
x
a
b
y ±=

38. Conics Parabola Ellipse Hyperbola
Graph
Parametric
representation
of P )2,( 2
atat )sin,cos( θθ ba )tan,sec( θθ ba