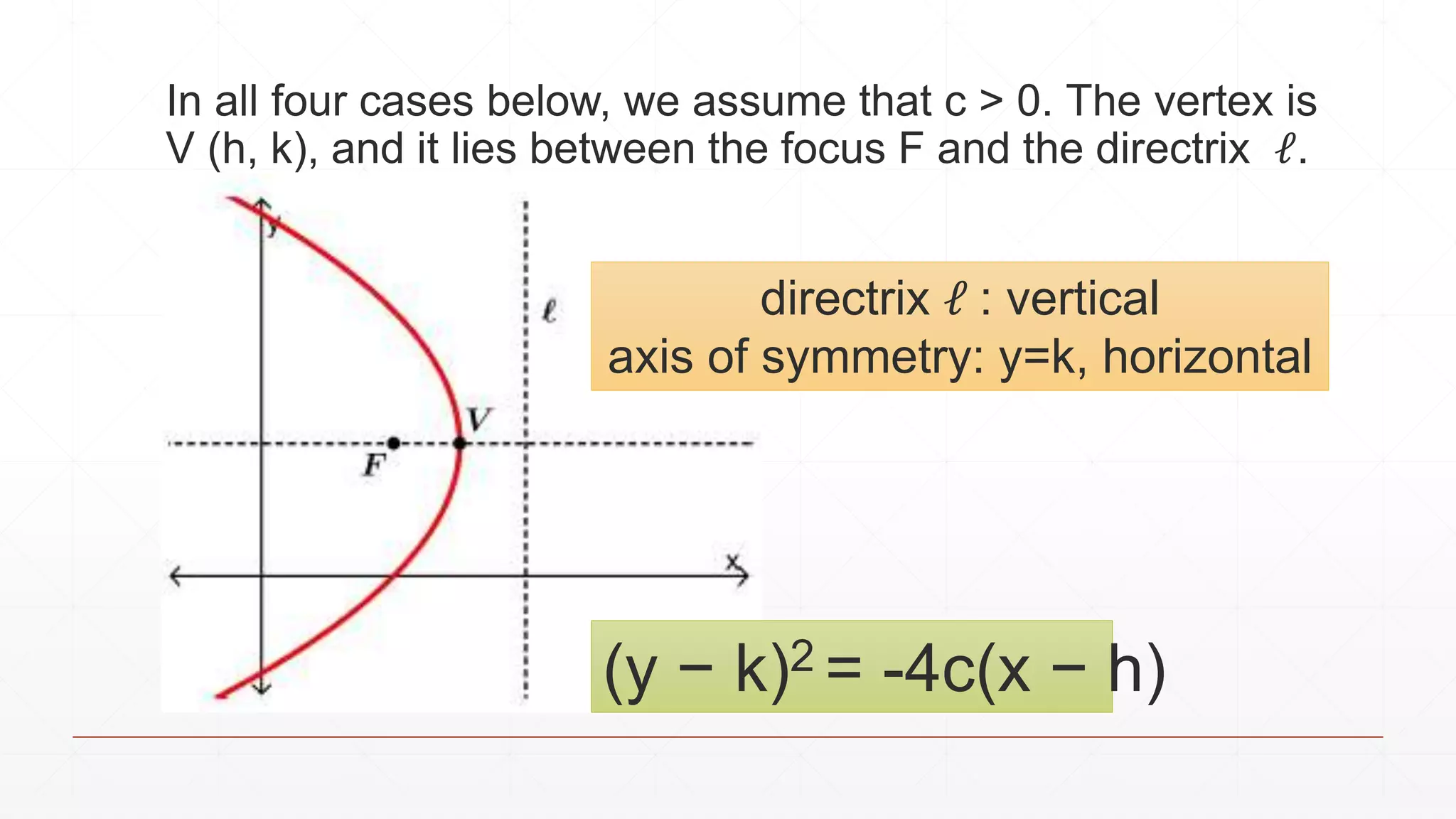
This document discusses properties of parabolas including: - The relationship between the focus and directrix of a parabola and any point on the parabola. - The standard form equations of parabolas depending on their orientation and location of the vertex. - Converting between standard, general, and vertex forms of parabolic equations. - Examples of determining the vertex, focus, directrix, and axis of symmetry from equations and vice versa.

1. Parabolas
More Properties of Parabolas
PRECALCULUS

2. More Properties of Parabolas
▪ Recall that, for any point on the parabola, its
distance from the focus is the same as its distance
from the directrix.

3. In all four cases below, we assume that c > 0. The vertex is
V (h, k), and it lies between the focus F and the directrix ℓ.
(x − h)2 = 4c(y − k)
directrix ℓ : horizontal
axis of symmetry: x=h, vertical

4. In all four cases below, we assume that c > 0. The vertex is
V (h, k), and it lies between the focus F and the directrix ℓ.
(x − h)2 = - 4c(y − k)
directrix ℓ : horizontal
axis of symmetry: x=h, vertical

5. In all four cases below, we assume that c > 0. The vertex is
V (h, k), and it lies between the focus F and the directrix ℓ.
(y − k)2 = 4c(x − h)
directrix ℓ : vertical
axis of symmetry: y=k, horizontal

6. In all four cases below, we assume that c > 0. The vertex is
V (h, k), and it lies between the focus F and the directrix ℓ.
(y − k)2 = -4c(x − h)
directrix ℓ : vertical
axis of symmetry: y=k, horizontal

7. Let’s try!
▪ If the parabola opens to the right, with vertex at the origin, the
equation is (a) x2 = 4cy
(b) x2 = -4cy
(c) y2 = -4cx
(d) y2 = 4cx

8. Let’s try!
▪ If the parabola opens to the right, with vertex at the origin, the
equation is (a) x2 = 4cy
(b) x2 = -4cy
(c) y2 = -4cx
(d) y2 = 4cx

9. Let’s try!
▪ If the parabola opens downward, with vertex at the origin, the
equation is (a) x2 = 4cy
(b) x2 = -4cy
(c) y2 = -4cx
(d) y2 = 4cx

10. Let’s try!
▪ If the parabola opens downward, with vertex at the origin, the
equation is (a) x2 = 4cy
(b) x2 = -4cy
(c) y2 = -4cx
(d) y2 = 4cx

11. Let’s try!
▪ If the parabola opens to the left, with vertex at the origin, the
equation is (a) x2 = 4cy
(b) x2 = -4cy
(c) y2 = -4cx
(d) y2 = 4cx

12. Let’s try!
▪ If the parabola opens to the left, with vertex at the origin, the
equation is (a) x2 = 4cy
(b) x2 = -4cy
(c) y2 = -4cx
(d) y2 = 4cx

13. Let’s try!
▪ If the parabola opens upward, with vertex at the origin, the
equation is (a) x2 = 4cy
(b) x2 = -4cy
(c) y2 = -4cx
(d) y2 = 4cx

14. Let’s try!
▪ If the parabola opens upward, with vertex at the origin, the
equation is (a) x2 = 4cy
(b) x2 = -4cy
(c) y2 = -4cx
(d) y2 = 4cx

15. Let’s try!
▪ If the parabola opens upward, with vertex (h,k), the equation
is (a) (x-h)2 = 4c(y-k)
(b) (x-h)2 = -4c(y-k)
(c) (y-k)2 = 4c(x-h)
(d) (y-k)2 = -4c(x-h)

16. Let’s try!
▪ If the parabola opens upward, with vertex (h,k), the equation
is (a) (x-h)2 = 4c(y-k)
(b) (x-h)2 = -4c(y-k)
(c) (y-k)2 = 4c(x-h)
(d) (y-k)2 = -4c(x-h)

17. Let’s try!
▪ If the parabola opens to the right, with vertex (h,k), is
(a) (x-h)2 = 4c(y-k)
(b) (x-h)2 = -4c(y-k)
(c) (y-k)2 = 4c(x-h)
(d) (y-k)2 = -4c(x-h)

18. Let’s try!
▪ If the parabola opens to the right, with vertex (h,k), is
(a) (x-h)2 = 4c(y-k)
(b) (x-h)2 = -4c(y-k)
(c) (y-k)2 = 4c(x-h)
(d) (y-k)2 = -4c(x-h)

19. Let’s try!
▪ If the parabola opens down, with vertex (h,k), the equation is
(a) (x-h)2 = 4c(y-k)
(b) (x-h)2 = -4c(y-k)
(c) (y-k)2 = 4c(x-h)
(d) (y-k)2 = -4c(x-h)

20. Let’s try!
▪ If the parabola opens down, with vertex (h,k), the equation is
(a) (x-h)2 = 4c(y-k)
(b) (x-h)2 = -4c(y-k)
(c) (y-k)2 = 4c(x-h)
(d) (y-k)2 = -4c(x-h)

21. Let’s try!
▪ If the parabola opens to the left, with vertex (h,k), is
(a) (x-h)2 = 4c(y-k)
(b) (x-h)2 = -4c(y-k)
(c) (y-k)2 = 4c(x-h)
(d) (y-k)2 = -4c(x-h)

22. Let’s try!
▪ If the parabola opens to the left, with vertex (h,k), is
(a) (x-h)2 = 4c(y-k)
(b) (x-h)2 = -4c(y-k)
(c) (y-k)2 = 4c(x-h)
(d) (y-k)2 = -4c(x-h)

23. Standard equation of a Parabola
▪ Example 1. The figure
shows the graph of
parabola, with only its
focus and vertex
indicated. Find its
standard equation. What
is its directrix and its axis
of symmetry?

24. Equation of the Parabola in General Form
▪The standard equation
(y +4)2 = −8(x−5),
be rewritten as
y2 + 8x + 8y − 24 = 0

25. The general equation of parabola is given by
𝐴𝑥2
+ 𝐶𝑥 + 𝐷𝑦 + 𝐸 = 0
(A and C are nonzero)
or
𝐵𝑦2
+ 𝐶𝑥 + 𝐷𝑦 + 𝐸 = 0
(B and C are nonzero)
Equation of the Parabola in General Form

26. Let’s try!
▪ Example 2. Determine the vertex, focus, directrix, and
axis of symmetry of the parabola with the given
equation. Sketch the parabola, and include these
points and lines.
(a) y2 − 5x + 12y = −16
(b) 5x2 + 30x + 24y = 51
▪ Example 3. A parabola has focus F(7, 9) and directrix
y = 3. Find its standard equation.

27. Seatwork
▪ 1. Determine the vertex, focus, directrix, and axis
of symmetry of the parabola with equation
x2−6x+5y = −34. Sketch the graph, and include
these points and lines.
▪ A parabola has focus F(−2,−5) and directrix x = 6.
Find the standard equation of the parabola.

28. THANK YOU
www.slideshare.net/reycastro1
@reylkastro2
reylkastro