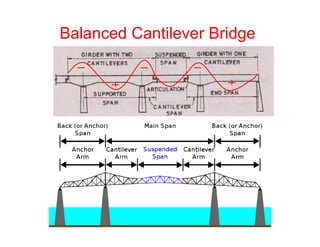
This document provides information on the structural design of bridges and culverts. It discusses the design of solid slab bridges, T-beam bridges, and balanced cantilever bridges. It also covers the distribution of live loads on bridge slabs using methods like Pigeaud's theory and Courbon's method. Finally, it summarizes the design process for box culverts, including determining load cases and calculating bending moments and reinforcement requirements.

1. Structural Design of bridge
and Culvert
SDE. Prabhat Kumar Jha
Department of Road
9841360244

2. Structural design of bridge:
• solid slab bridges, deck girder bridges, B.M. in slab
supported on four edges, distribution of live loads on
longitudinal beams, method of distribution
coefficients, Courbon’s method,
• design of a T- beam bridge, balanced cantilever bridge,
Design of box culvertDesign of box culvert

3. Solid Slab Bridge
Generally for Span <10m
The simplest form of R.C.C. bridges in which the deck
spans between the abutments as a simply supported
one-way slab.
Bending moments and shear force are determined
separately for dead load and live loads.
The design B.M, obtained by adding the B.M due to dead
loads and live load, governs the thickness of slab and
the area of main reinforcement.

4. • Solid Slab Bridge
The live load to be considered in the design of bridges
consists of concentrated wheel loads due to trains of
different types of heavy vehicles following each other
closely (viz, class AA, class A or class B loading).
The analysis of a slab spanning in one or two directions andThe analysis of a slab spanning in one or two directions and
carrying concentrated load may be carried out by any one of
the rational method like
(i)Pigeaud’s theory
(ii)Westergaurd’s method and
(iii)Effective width method.

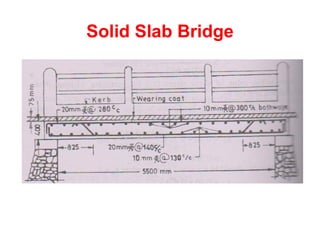
5. • Solid Slab Bridge
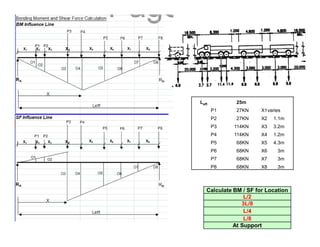
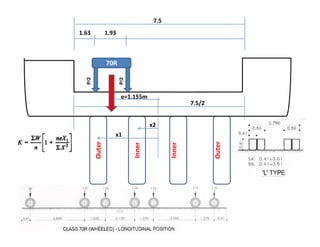
7.5m1m W W
Dead Load Bending Moment = w l2 / 8
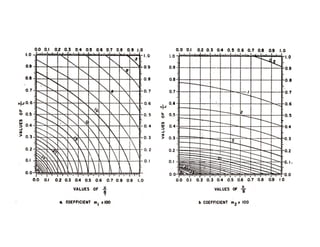
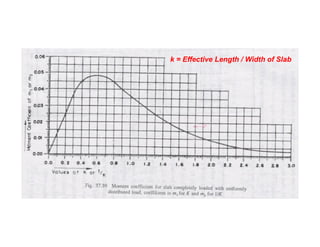
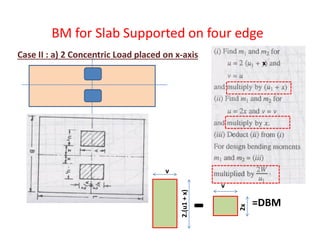
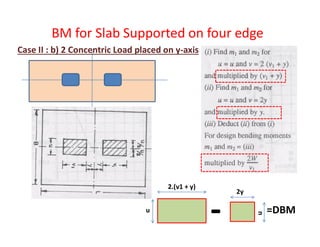
Live Load Bending Moment by Pigeaud’s theory/Curve
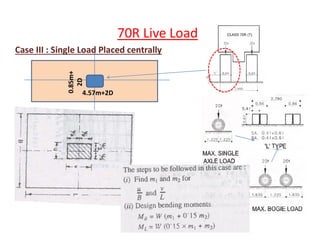
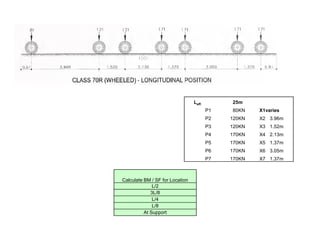
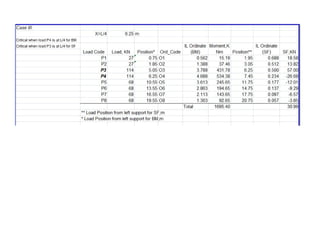
10m
Effective depth required :
d = Sqrt [BM / (R x b)]
Area of Reinforcement required
:
= M / (j x d x σst )
R = Moment of Resistance factor
= 0.5 (σcbc . j . K)
d = effective depth
j = lever arm factor = (1- k/3)
k = neutral axis factor = n/d
= (m. σcbc )/(m. σcbc + σst )
σst = 240 N/mm2 for fy = 500 N/mm2

6. Solid Slab Bridge

7. T-BEAM Bridge “Deck Girder Bridge”
Generally for Span >10m to 25m
The deck Slab is cast monolithically with Longitudinalmonolithically with Longitudinal
GirdersGirders
Design involves :
Design of Deck Slab : Pigeaud’s theory
Design of Longitudinal Girder : Courbon's Method for Live Load
Moment and Shear Force calculation
Design of Cross Girders : Simple Beam Analysis

8. BM for Slab Supported on four edge
Traffic Direction
Case I : Single Load Placed centrally
Case II : a) 2 Concentric Load placed on x-axis
x
y
L
B = Short Span
Case II : b) 2 Concentric Load placed on y-axis

9. BM for Slab Supported on four edge
B
b
W
u=W+2D
W
u
v
v= b+ 2D
X-X
L
b
Slab Depth ,D
b

10. BM for Slab Supported on four edge
Case I : Single Load Placed centrally
x
y
Using Pigeaud’s Graph :
Load Placing must be
symmetrical
k = Width of Slab/Effective
Length /
For given k, related u/B Vs v/L :-
m1 and m2 determined
. IF
. IF

12. k = Effective Length / Width of Slab

13. BM for Slab Supported on four edge
Case II : a) 2 Concentric Load placed on x-axis
x
2.(u1+x) v
=DBM
2x
v

14. BM for Slab Supported on four edge
Case II : b) 2 Concentric Load placed on y-axis
u
2.(v1 + y)
u
2y
=DBM

15. 70R Live Load
Case III : Single Load Placed centrally
0.85m+
2D
4.57m+2D

16. Class A Live Load
Case IIb
1 2
0.5m+2D
1.2m
=DBM
3
Imaginary
(For Wheel 1,3 case )/2 + Wheel 2 case
1.2m
0.25m+2D
=DBM(For Wheel 1,3 case )/2 + Wheel 2 case

17. Longitudinal Analysis

18. Calculate BM / SF for Location
L/2
3L/8
L/4
L/8
At Support

19. Leff. 25m
P1 27KN X1varies
P2 27KN X2 1.1m
P3 114KN X3 3.2m
P4 114KN X4 1.2m
P5 68KN X5 4.3m
P6 68KN X6 3m
P7 68KN X7 3m
P8 68KN X8 3m
Calculate BM / SF for Location
L/2
3L/8
L/4
L/8
At Support

20. Leff. 25m
P1 80KN X1varies
P2 120KN X2 3.96m
P3 120KN X3 1.52m
P4 170KN X4 2.13m
P5 170KN X5 1.37m
P6 170KN X6 3.05m
P7 170KN X7 1.37m
Calculate BM / SF for Location
L/2
3L/8
L/4
L/8
At Support

22. COURBON'S METHOD FOR ESTIMATING DISTRIBUTION
COEFFICIENTS
Courbon's method :
According to Courbon's method,
The reaction Ri of the cross beam on any girder I of a typical
bridge consisting of multiple parallel beam is computed
assuming a linear variation of deflection in the transverseassuming a linear variation of deflection in the transverse
direction.
The deflection will be maximum on the exterior girder on the
side of the eccentric load or e.g. of loads if there is a system of
concentrated loads) and minimum of the other exterior girder.

23. Assumptions or Conditions for Applicability of Courbon's method :
• Simply put, this method for transverse load distribution
among the deck longitudinal is applicable mainly to beam and
slab type decks which are straight in plan (no skew and no
curve).
• The longitudinal beams must be interconnection by
symmetrically spaced, rigid cross beams that are at least five
in number (one above each support, and at least three
intermediate cross beams, equally spaced) ,such that they are
in number (one above each support, and at least three
intermediate cross beams, equally spaced) ,such that they are
not more than about 9 m apart.
• The cross beams should preferably be cast monolithically
with the longitudinal or should be cast at least before any
other gravity loads (besides the self weight of the main
beams) comes on. The stiffness of cross girders is much
greater than that of the longitudinal girders.

24. Assumptions or Conditions for Applicability of Courbon's
method :
• The ratio of span to width is greater than 2 but less than 4 i.e.
the bridge should be longish.
• spacing between main beams should be between 2 and 4.
• The cross girders extend to a depth of at least 0.75 of the
depth of the longitudinal girders. This is done so as to avoid
• The cross girders extend to a depth of at least 0.75 of the
depth of the longitudinal girders. This is done so as to avoid
anchoring of steel which may interfere with the main steel.
• The bridge structure may have longitudinal girders of same or
different moment of inertia and may have uniform or non -
uniform girder spacing.
• Under the effect of loading, the transverse profile of the
bridge deck maintains a straight geometry.

25. • These conditions are usually satisfied for majority of modern T-beams bridges.

26. IRC Class A
IRC Class A
P/2=114/2
P/2=114/2
P/2=114/2
P/2=114/2
IRC Class A
0.4 1.8 1.81.7
7.5
7.5/2
2P
e=0.7m
x2
Inner
Inner
Outer
Outer
x1
x2

27. 1.63 1.93
7.5
7.5/2
e=1.155m
x2
70R
P/2
P/2
Inner
Inner
Outer
Outer
x1
x2

28. Sample

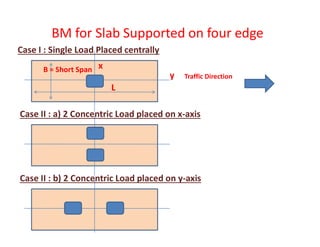
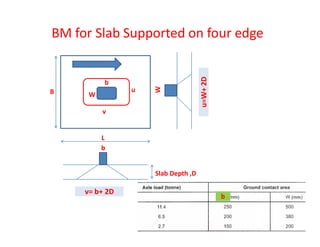
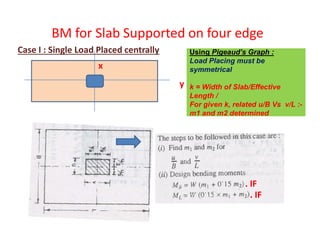
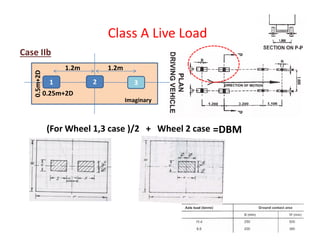
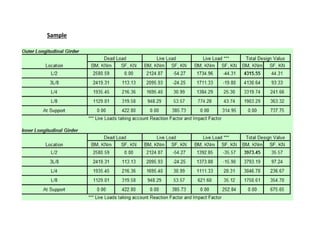
29. T-Beam Designed as Singly Reinforced Beam
Effective depth required :
d = Sqrt [BM / (R x b)]
Area of Reinforcement required :
= M / (j x d x σst )
R = Moment of Resistance factor
= 0.5 (σcbc . j . K)
d = effective depth
j = lever arm factor = (1- k/3)
k = neutral axis factor = n/d
= (m. σcbc )/(m. σcbc + σst )
σst = 240 N/mm2 for fy = 500 N/mm2
σcbc= fck /3

31. Moment of Resistance > Design BM

32. Balanced Cantilever Bridge

33. •Design of Box Culvert
It is RCC rigid frame box culverts with square or
rectangular opening.
If 4m Span limit and height max. 3m for economy
If Q is low and Bearing Capacity is also low : Box Culvert
is preferred rather than Slab Culvert
The Top of Box Section can be at road level or can be at a
depth below.
Box is structurally very strong, rigid and safe.
Box does not need any elaborate foundation and can
easily be placed over soft foundation by increasing base
slab projection to retain base pressure within safe
bearing capacity of ground soil.

34. Design of Box Culvert
• V1 = Uniform Vertical Load due to Slab, Wearing Coat and or Wt. of Soil above
• V2 = Reaction of V3 and or Weight of water
• V3 = Wt. of Wall

35. Design of Box Culvert
• V4 = Concentrated vertical Load of Wheel = V x I / e
P = Wheel load
I = Impact factor
e = effective width of dispersion
• H1 = Earth Pressure by Coloumb’s Theory
• H2 = Water Pressure inside box =  x H
• H3 = Live load surcharge = q x Ka x ( H + Free Board )

36. •Design of Box Culvert
Loading Case
Mainly three load cases govern the design. These are
given below :
a) Box empty, live load surcharge on top slab of box
and superimposed surcharge load on earth fill.
b) Box inside full with water, live load surcharge onb) Box inside full with water, live load surcharge on
top slab and superimposed surcharge load on earth
fill.
c) Box inside full with water, live load surcharge on
top slab and no superimposed surcharge on earth
fill.

37. Design of Box Culvert
The bending moment is obtained by
moment distribution considering all the cell
or cells together for different combination
of loading and design of section
accomplished for final bending momentsaccomplished for final bending moments
for that member.

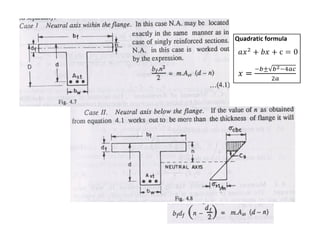
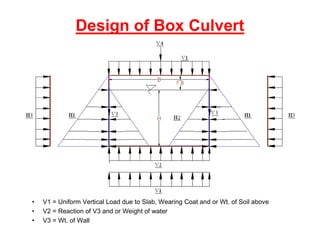
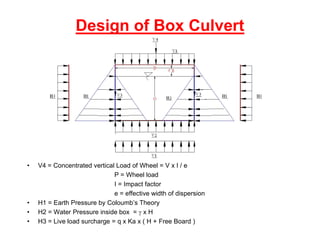
38. EffectivedepthrequiredforWallorSlab
d=Sqrt[BM/(Rx1000)]mm
AreaofReinforcementrequiredforWallorSlab
=M/(jxdx
EffectivedepthrequiredforWallorSlab
d=Sqrt[BM/(Rx1000)]mm
AreaofReinforcementrequiredforWallorSlab
=M/(jxdxσst)