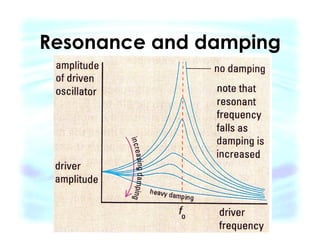
This document discusses free and forced vibrations, including undamped and damped oscillators, resonance, and types of damping. It provides examples of resonance in swinging, tuning a radio, musical instruments, machinery, and chemical bonds. Damping can limit resonant amplitude by transferring energy away. The Q-factor measures damping, with light damping having a large Q-factor and heavy damping a small one. Unwanted resonance can be destructive, and is addressed through damping, changing natural frequencies, or stiffness.

1. free and forced vibrations

2. Free oscillators Undamped oscillator Natural frequency,  o No external forces e.g. swing

3. Forced oscillators External forces act on oscillator Forced/driven oscillator Resonance: driving  =  o e.g. loudspeaker vibrates in response to oscillating electric signal (driver) Barton's pendulums

4. Problems Resonance driver applies forces that continually supply energy to oscillator  increasing amplitude A increases indefinitely unless energy transferred away Severe case: A limit reached when oscillator destroys itself e.g. wine glass shatters when opera singer reaches particular note

5. Damping Resonant Amplitude limited by damping forces At resonance: rate of energy supply = WD against damping forces Increasing damping reduces sharpness + strength of resonance

6. Types of damping Oscillating masses lose energy  amplitude decreases Light damping: amplitude decreases gradually Critical damping: amplitude decreases can decrease to zero without oscillation. Minimum time = T/4

7. Q-factors Measure of resonance Definition: number free oscillations a free oscillator competes before decaying to zero * Light damping = large Q factor Heavy damping = small Q factor e.g. Car = 1 Guitar string = 10 3 Watch quartz crystal = 10 5 * This is only an approximation. Q-factor does have a complicated precise mathematical definition

8. Resonance and damping

9. Examples Pushing a child on a swing – maximum A when pushing  =  o Tuning a radio – electrical resonance occurs when  o of tuning circuit adjusted to match  of incoming signal Pipe instruments - column of air forced to vibrate. If reed  =  o of column loud sound produced Rotating machinery – e.g. washing machine. An out of balance drum will result in violent vibrations at certain speeds

10. Investigation strength of chemical bonds – EM radiation = oscillating electrical disturbance. When incident on a crystal ions subjected to oscillating electrical force. At correct frequency ions ions oscillated by resonance Energy is absorbed from radiation, the frequency of which can be measured with a spectrometer

11. Unwanted resonance Structures/machinery Results in destruction Damping Changing  o of object by changing its mass Change stiffness of supports (  moving resonant  away from driving  )

12. Model aircraft being tested for resonance in a wind tunnel