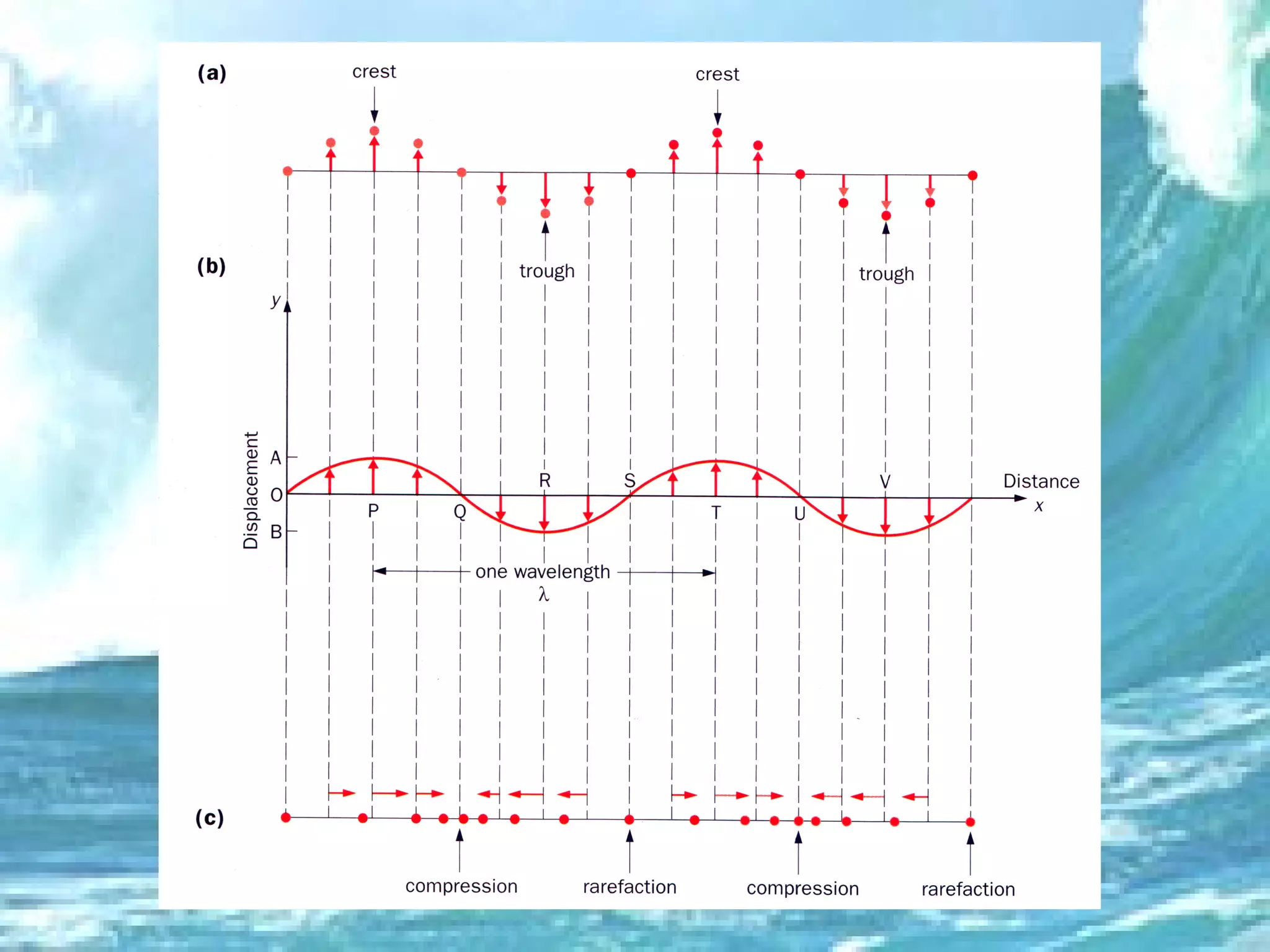
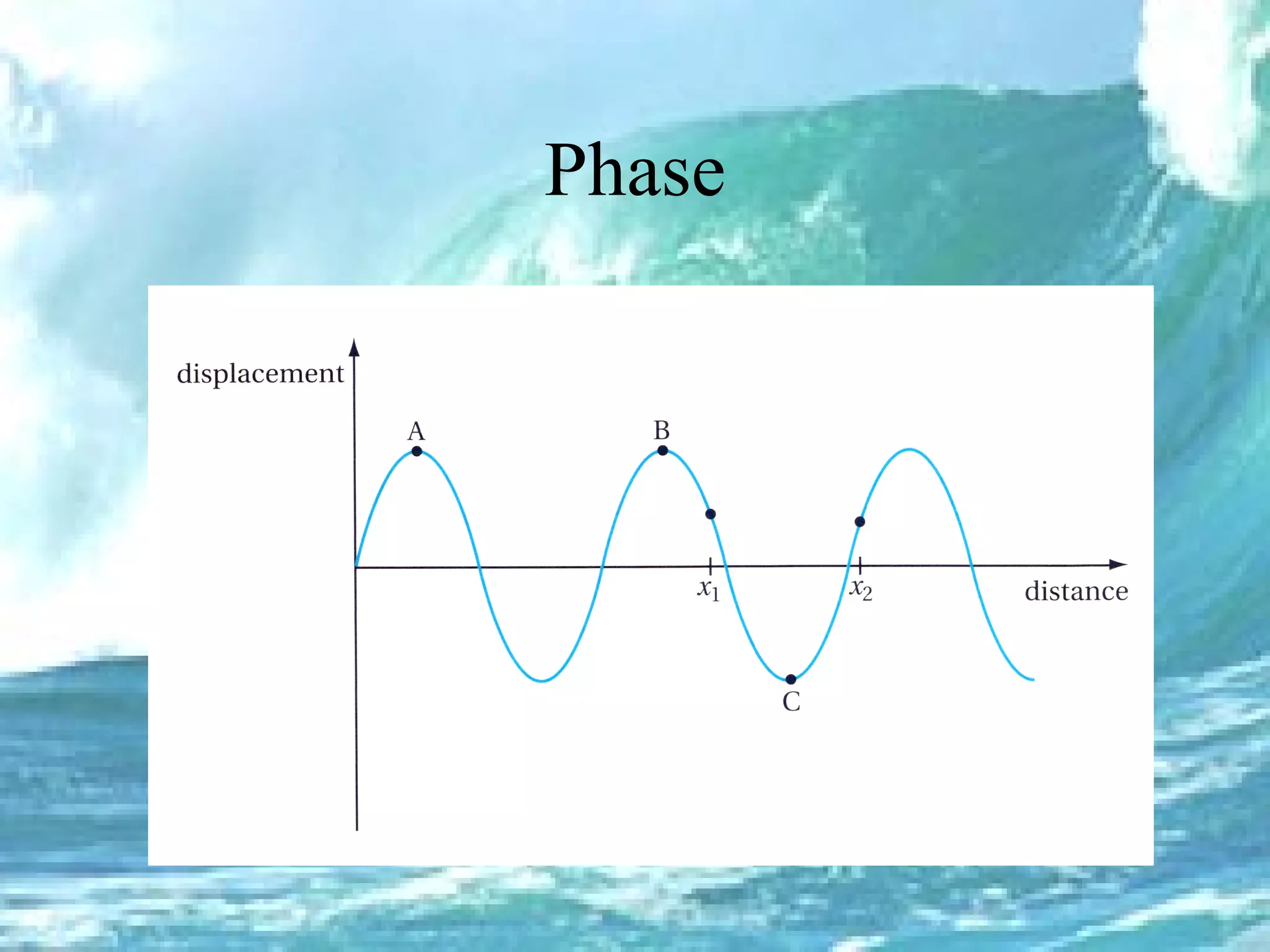
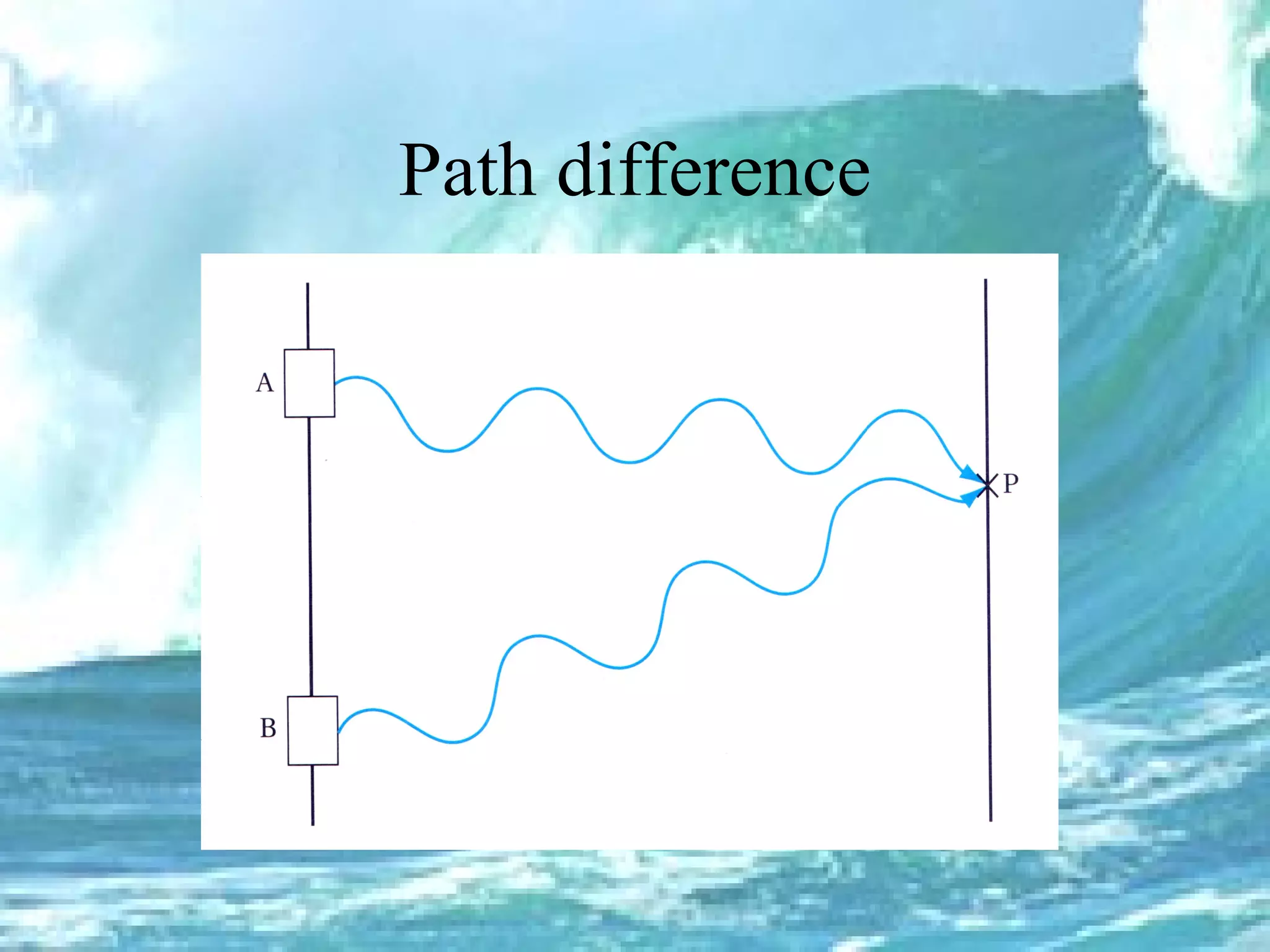
1. The document discusses progressive waves, which are waves that transfer energy and information through a medium from one point to another. 2. It defines key wave properties such as amplitude, wavelength, frequency, phase, and path difference which are used to describe and analyze wave behavior. 3. Graphs and equations are presented that show the relationships between wavelength, frequency, wave speed, phase difference, and path difference which determine whether waves will constructively or destructively interfere when they meet.

1. Progressive waves

2. “ Looking out into the immensity of the universe, we stand at the shores of the cosmic ocean. Yet our earthly seas are no less beautiful, and the crashing surf reminds us that most of what we know about our world comes from information carried by waves.” Carl Sagan

3. Waves A basic concept of physics Progressive waves Describing waves Longitudinal Transverse

4. Graphical representation Displacement - time graph Transverse mechanical wave Longitudinal wave Amplitude Wavelength Frequency

6. Wavelength, frequency and wave speed A wave source vibrates at f vibrations per second  particles of transmitting medium vibrate at same frequency 1 complete vibration = 1 wave generated  disturbance =  m from source   = f  or c = f  Note: this is not on data sheet

7. Phase

8. A and B: in phase B and C: in antiphase Phase difference  Calculating  for x 1 and x 2  = 2  ( x 1 - x 2 )  If x 1 - x 2 integer number  s,  = 2  , 4  , 6  etc

9. Path difference

10. Waves emitted from a and B in phase At P: relative phase depends on distance travelled Path difference = BP – AP Path difference = n   constructive Path difference = (n + ½ )   destructive