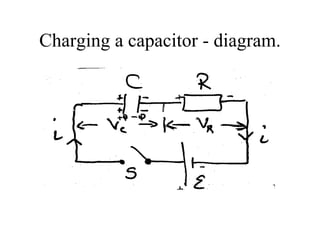
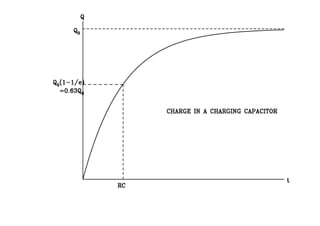
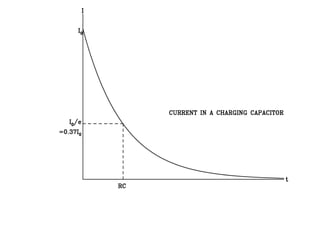
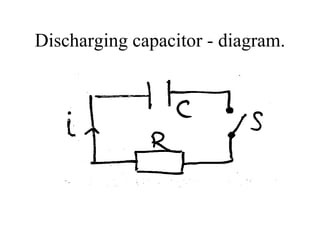
This document discusses charging and discharging capacitors in circuits. When a capacitor is charging, current flows through the circuit and decreases over time as charge builds up on the capacitor. The time it takes for the charge to reach 63% of its final value is called the time constant, represented by τ, which equals the resistance R multiplied by the capacitance C. When discharging, the current direction reverses but also decreases over time as the stored charge depletes from the capacitor. The energy stored in the capacitor is 1/2 CV^2 and equals the work done by the battery during charging.

2. Charging a capacitor - diagram.

10. Discharging capacitor - diagram.