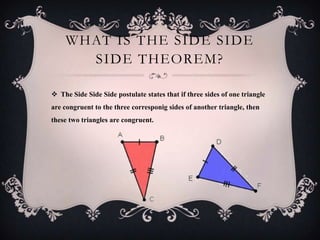
The document discusses the Side-Side-Side (SSS) theorem of geometry. It provides background on theorems and their origins in Greek mathematics. The SSS theorem states that if three sides of one triangle are congruent to three sides of another triangle, the triangles are congruent. Euclid first proved this theorem. Everyday examples of using the SSS theorem are given, such as determining if two windows are the same shape. A formal proof using labeled triangles is provided to demonstrate the SSS theorem.

1. SSS THEOREM
Lucia Artigas
9-2 20.3

2. OUTLINE
2. 
3. Introduccion to Theorems
4. Biography of Euclid creator of the SSS
5. Why Euclid creat The SSS 
6. What is the SSS theorem? 
7. Defenitions for understanding
8. Every day uses…
9. Examples 1
10. A Side Side Side Proof
11. Bibliogrfphy

3. INTRODUCCION TO
THEOREMS
 theorem (noun), theory (noun), theoretical (adjective): from
Greek theorema, fromtheorein "to look at," of unknown origin .
 In mathematics, after studying a situation or a class of objects, a
person hopes to make speculations and then prove them, so theorem
came to mean the proof of a speculation that has been arrived at by
looking at something.

4. BIOGRAPHY OF EUCLID
CREATOR OF THE SSS
The Father of Geometry
Records show that he lived
somewhere around 300 B.C. He was a
Greek, most historians believe Euclid was
educated at Athens. His teachers may have
included pupils of Plato, who was a
philosopher and one of the most
influential The first printed edition of
Euclid's works was a translation from Arabic
to Latin, which appeared at Venice in 1482.

5. WHY EUCLID CREAT THE
SSS 
 Euclid proved his Side-Side-Side (SSS) Theorem (I.8) and his Angle-
Side-Angle (ASA, diagram at the right) Theorem (I.26) in a similar
way. In SSS, if a triangle has all three sides conguent to the
corresponding sides of a second triangle, then they are congruent.

6. WHAT IS THE SIDE SIDE
SIDE THEOREM?
 The Side Side Side postulate states that if three sides of one triangle
are congruent to the three corresponig sides of another triangle, then
these two triangles are congruent.

7. DEFENITIONS FOR
UNDERSTANDING
 Def. Congruence: In Plane Geometry, two objects are congruent if all of
their corresponding parts are congruent
 Def. Corresponding Parts: n. in congruent polygons (Triangles), the pairs
of sides which can be superimposed on one another.
 Note: In the above, I used the term "congruent" instead of "equal" when
comparing sides and angles. Numbers are equal. Line segments (sides) and
angles are congruent. Calling them "equal" is a sloppy way of saying that
their measures (lengths or sizes)

8. EVERY
DAY USES… 
 For Geometry Class with Miss H. in the subject of Math
 If I want it to know if the 2 triangular windows are congruent
triangles, for it to be symmetric and nice to decorate my house .
 To measure triangles faster because I know that if the sides are
equal they are congruent an their angles are congruent too, so i don’t
need to use a protractor an do every thing easier.

9. Example 1
 ABC XYZ
 Alll 3 sides are congruent
• ZX = CA (side)
• XY = AB (side)
• YZ = BC (side)
 Therefore, by the Side Side Side postulate, the triangles are congruent

10. A SIDE SIDE SIDE PROOF
Midpoint

11. RFERENCES
Bibliogrfphy
1. http://www.cut-the-knot.org/WhatIs/WhatIsTheorem.shtml
 E. J. Borowski & J. M. Borwein, The Harper Collins Dictionary of
Mathematics, Harper Perennial, 1991
2. http://www.mathwarehouse.com/geometry/congruent_triangles/side-
side-side-postulate.php